Кусочно-линейная функция

Пусть заданы ${\displaystyle x_{1}<x_{2}<\ldots <x_{n}}$ — точки смены формул.

Как и все кусочно-заданные функции, кусочно-линейную функцию обычно задают на каждом из интервалов ${\displaystyle (-\infty ;x_{1}),(x_{1};x_{2});\ldots (x_{n};+\infty )}$ отдельной формулой. Записывают это в виде: ${\displaystyle f(x)={\begin{cases}k_{0}x+b_{0},\quad x<x_{1}\\k_{1}x+b_{1},\quad x_{1}<x<x_{2}\\\cdots \\k_{n}x+b_{n},\quad x_{n}<x\end{cases}}}$

Если к тому же выполнены условия согласования

${\displaystyle k_{i}x_{i}+b_{i}=k_{i+1}x_{i}+b_{i+1}=f(x_{i})}$ при ${\displaystyle i=1,2,\ldots ,n-1}$,

то кусочно-линейная функция будет непрерывной. Непрерывная кусочно-линейная функция называется также линейным сплайном.

Можно доказать, что любую непрерывную кусочно-линейную функцию можно задать некоторой формулой вида

${\displaystyle f(x)=ax+b+c_{1}|x-x_{1}|+c_{2}|x-x_{2}|+\ldots +c_{n}|x-x_{n}|}$.

При этом все коэффициенты, кроме b, можно выразить через угловые коэффициенты наклона прямых на отдельных интервалах:

${\displaystyle c_{i}={\frac {k_{i}-k_{i-1}}{2}}}$, при ${\displaystyle i=1,2,\ldots ,n}$

${\displaystyle a={\frac {k_{0}+k_{n}}{2}}}$

• Любую непрерывную функцию можно аппроксимировать сколь угодно близко кусочно-линейной функцией (в непрерывной метрике).

График кусочно линейной функции

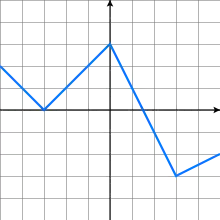
График функции на рисунке аналитически задан в виде:

${\displaystyle f(x)={\begin{cases}-x-3&{\text{если}}\ x\leq -3\\x+3&{\text{если}}\ -3<x<0\\-2x+3&{\text{если}}\ 0\leq x<3\\0,5x-4&{\text{если}}\ x\geq 3\end{cases}}}$

• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 272-274. — 383 с. — ISBN 5-09-001287-3.
• Кусочно-линейная функция // Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

• Задачи по теме: Кусочно-линейные функции.