Кусочно-заданная функция
Кусо́чно-за́данная фу́нкция — функция одной переменной, определённая на множестве вещественных чисел, которая задана отдельной формулой (или другим способом задания функции) на каждом из интервалов, составляющих область её определения.
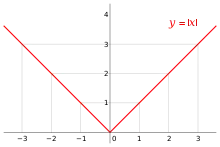
График функции модуля вещественной переменной — пример кусочно-заданной (кусочно-линейной) функции
Кусочно-аффинная функция - это числовая функция от одной переменной такая , что всю её область определения можно "разделить" на промежутки так , что на внутренности каждого из промежутков функция аффинная .
Формальное определение и задание
Пусть заданы — точки смены задания функции.
Кусочно-заданные функции обычно задают на каждом из интервалов отдельно. Формально записывают это в виде:
.
На некоторых из интервалов в общем случае кусочно-заданная функция может быть не определена.
Виды кусочно-заданных функций
- Если все функции — постоянные, то — кусочно-постоянная функция.
- Если все функции являются линейными функциями, то — кусочно-линейная функция.
- Если все функции являются непрерывными функциями, то — кусочно-непрерывная функция. При этом сама она может не являться непрерывной.
- Если все функции являются дифференцируемыми функциями, то — кусочно-гладкая функция. При этом точки смены функций могут быть, а могут и не быть точками излома.
- Если все функции являются монотонными функциями, то — кусочно-монотонная функция. При этом на соседних интервалах знак первой производной может быть разный, то есть нарастающие или падающие функции.
Примеры часто используемых кусочно-заданных функций
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.