Динамическое программирование

Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Ричардом Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. В 1953 году он уточнил это определение до современного. Первоначально эта область была основана, как системный анализ и инжиниринг, которая была признана IEEE. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.

Слово «программирование» в словосочетании «динамическое программирование» в действительности к «традиционному» программированию (написанию кода) почти никакого отношения не имеет и имеет смысл как в словосочетании «математическое программирование», которое является синонимом слова «оптимизация». Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи. К примеру, определённое расписание событий на выставке иногда называют программой. Программа в данном случае понимается как допустимая последовательность событий.

Нахождение кратчайшего пути в графе из одной вершины в другую, используя оптимальную подструктуру; прямая линия обозначает ребро между вершинами; волнистая линия обозначает кратчайший путь между вершинами, которые она соединяет (среди других путей, которые не показаны; промежуточные вершины кратчайшего пути тоже не показаны); жирной линией обозначен итоговый кратчайший путь.

Граф подзадач (ребро означает, что одна задача зависит от решения другой) для чисел Фибоначчи (граф — ациклический).

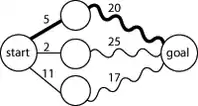
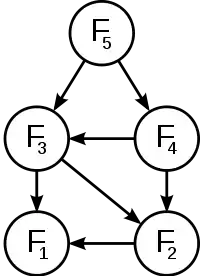
Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса рёбер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.

1. Разбиение задачи на подзадачи меньшего размера.
2. Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.
3. Использование полученного решения подзадач для конструирования решения исходной задачи.

Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д., пока не приходят к тривиальному случаю задачи, решаемой за константное время (ответ можно сказать сразу). К примеру, если нам нужно найти n!, то тривиальной задачей будет 1! = 1 (или 0! = 1).

Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи, ${\displaystyle F_{3}=F_{2}+F_{1}}$ и ${\displaystyle F_{4}=F_{3}+F_{2}}$ — даже в таком тривиальном случае вычисления всего двух чисел Фибоначчи мы уже посчитали ${\displaystyle F_{2}}$ дважды. Если продолжать дальше и посчитать ${\displaystyle F_{5}}$, то ${\displaystyle F_{2}}$ посчитается ещё два раза, так как для вычисления ${\displaystyle F_{5}}$ будут нужны опять ${\displaystyle F_{3}}$ и ${\displaystyle F_{4}}$. Получается следующее: простой рекурсивный подход будет расходовать время на вычисление решения для задач, которые он уже решал.

Чтобы избежать такого хода событий, мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется мемоизацией. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив её для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, ещё не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.

Подводя итоги вышесказанного можно сказать, что динамическое программирование пользуется следующими свойствами задачи:

• перекрывающиеся подзадачи;
• оптимальная подструктура;
• возможность запоминания решения часто встречающихся подзадач.

Динамическое программирование обычно придерживается двух подходов к решению задач:

• нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений уже решенных подзадач.
• восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.

Языки программирования могут запоминать результат вызова функции с определённым набором аргументов (мемоизация), чтобы ускорить «вычисление по имени». В некоторых языках такая возможность встроена (например, Scheme, Common Lisp, Clojure, Perl, D), а в некоторых требует дополнительных расширений (C++).

Известны сериальное динамическое программирование, включённое во все учебники по исследованию операций, и несериальное динамическое программирование (НСДП), которое в настоящее время слабо известно, хотя было открыто в 1960-х годах.

Обычное динамическое программирование является частным случаем несериального динамического программирования, когда граф взаимосвязей переменных — просто путь. НСДП, являясь естественным и общим методом для учёта структуры задачи оптимизации, рассматривает множество ограничений и/или целевую функцию как рекурсивно вычислимую функцию. Это позволяет находить решение поэтапно, на каждом из этапов используя информацию, полученную на предыдущих этапах, причём эффективность этого алгоритма прямо зависит от структуры графа взаимосвязей переменных. Если этот граф достаточно разрежен, то объём вычислений на каждом этапе может сохраняться в разумных пределах.

Одним из основных свойств задач, решаемых с помощью динамического программирования, является аддитивность. Неаддитивные задачи решаются другими методами. Например, многие задачи по оптимизации инвестиций компании являются неаддитивными и решаются с помощью сравнения стоимости компании при проведении инвестиций и без них.

• Задача о наибольшей общей подпоследовательности: даны две последовательности, требуется найти самую длинную общую подпоследовательность.
• Задача поиска наибольшей увеличивающейся подпоследовательности: дана последовательность, требуется найти самую длинную возрастающую подпоследовательность.
• Задача о редакционном расстоянии (расстояние Левенштейна): даны две строки, требуется найти минимальное количество стираний, замен и добавлений символов, преобразующих одну строку в другую.
• Задача о вычислении чисел Фибоначчи
• Задача о порядке перемножения матриц: даны матрицы ${\displaystyle A_{1}}$, …, ${\displaystyle A_{n}}$, требуется минимизировать количество скалярных операций для их перемножения.
• Задача о выборе траектории
• Задача последовательного принятия решения
• Задача об использовании рабочей силы
• Задача управления запасами
• Задача о рюкзаке: из неограниченного множества предметов со свойствами «стоимость» и «вес» требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при ограниченном суммарном весе.
• Алгоритм Флойда — Уоршелла: найти кратчайшие расстояния между всеми вершинами взвешенного ориентированного графа.
• Алгоритм Беллмана — Форда: найти кратчайший путь во взвешенном графе между двумя заданными вершинами.
• Максимальное независимое множество вершин в дереве: дано дерево, найти максимальное множество вершин, никакие две из которых не связаны ребром.
• Задача о расписании работы конвейера: есть два конвеера, по ${\displaystyle n}$ рабочих мест. Заданы времена работы на каждом конвеере, постановка на него и снятие, а также время передвижение на соседнее место. Требуется определить самый быстрый способ сборки детали, используя оба конвеера.

• Беллман Р. Динамическое программирование. — М.: Издательство иностранной литературы, 1960.
• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 15. Динамическое программирование // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4.
• Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh Vazirani. Algorithms = Algorithms. — 1-е изд. — McGraw-Hill Science/Engineering/Math, 2006. — С. 336. — ISBN 0073523402.
• Акулич И. Л. Глава 4. Задачи динамического программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9..
• Bertele U., Brioshi F. Nonserial dynamic programming. — N. Y.: Academic Press, 1972. — 235 pp.
• Габасов Р., Кириллова Ф. М. Основы динамического программирования. — Мн.: Изд-во БГУ, 1975. — 262 с.

• Видео лекции о динамическом программировании
• Теория, задачи, тестирующая система.