Гипотеза Хадвигера (теория графов)

В графе, раскрашенном в 4 цвета, отмечены 4 подграфа, между любыми двумя из них есть ребро

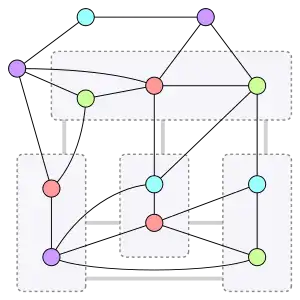
Гипотезу Хадвигера можно сформулировать иначе: в каждом ${\displaystyle k}$-хроматическом графе обязательно существует ${\displaystyle k}$ непересекающихся связных подграфов таких, что между любыми двумя из них есть ребро.

Если ввести для графа число Хадвигера ${\displaystyle h(G)}$ — максимальное ${\displaystyle k}$ такое, что ${\displaystyle G}$ стягиваем к полному графу на ${\displaystyle k}$ вершинах, то гипотеза формулируется в виде неравенства ${\displaystyle \chi (G)\leqslant h(G)}$, где ${\displaystyle \chi (G)}$ — хроматическое число графа.

Случаи ${\displaystyle k=2}$ и ${\displaystyle k=3}$ очевидны: в первом случае граф содержит хотя бы одно ребро, которое и является полным графом ${\displaystyle K_{2}}$, во втором случае граф не является двудольным и содержит цикл, стягиваемый к ${\displaystyle K_{3}}$.

Доказательство в случае ${\displaystyle k=4}$ было опубликовано самим Хадвигером в той же работе, в которой была поставлена гипотеза.

Из гипотезы Хадвигера в случае ${\displaystyle k=5}$ следует справедливость проблемы четырёх красок (ныне доказанной): операция стягивания сохраняет планарность, и, если бы существовал планарный 5-хроматический граф, то существовало бы вложение графа ${\displaystyle K_{5}}$ в плоскость, несуществование которого следует из формулы Эйлера. В 1937 году Клаус Вагнер доказал равносильность проблемы четырёх красок и гипотезы Хадвигера при ${\displaystyle k=5}$, таким образом, этот случай также доказан.

В 1993 году Н. Робертсон, П. Сеймур и Робин Томас доказали гипотезу для ${\displaystyle k=6}$, используя проблему четырёх красок.[1] Это доказательство получило премию Фалкерсона в 1994 году.

Для ${\displaystyle k=7}$ известно, что если граф не удовлетворяет гипотезе, то он стягиваем и к ${\displaystyle K_{4,4}}$, и к ${\displaystyle K_{3,5}}$ — полным двудольным графам с долями мощности 4 и 4 и мощности 3 и 5 соответственно.

Можно определить отображение ${\displaystyle h(G)}$, сопоставляющее графу ${\displaystyle G}$ максимальное ${\displaystyle k}$ такое, что ${\displaystyle G}$ стягиваем к полному графу на ${\displaystyle k}$ вершинах. Нахождение числа Хадвигера данного графа — NP-трудная задача. В любом графе ${\displaystyle G}$, для которого ${\displaystyle h(G)=k}$, существует вершина степени ${\displaystyle O(k{\sqrt {\log k}})}$.[2] Применяя жадный алгоритм для раскраски графа, из этого утверждения можно вывести, что ${\displaystyle \chi (G)=O(h(G){\sqrt {\log h(G)}})}$.

• Гипотеза Хадвигера (комбинаторная геометрия)