Магма (алгебра)
Магма (группоид) в общей алгебре — алгебра, состоящая из множества М с одной бинарной операцией M × M → M. Помимо требования замкнутости множества относительно заданной на нём операции, других требований к операции и множеству не предъявляется.
Термин «магма» был предложен Бурбаки. Термин «группоид» старше, он предложен Ойстином Оре, однако этот термин также относится к другой общеалгебраической структуре — теоретико-категорному группоиду, и в более современной литературе чаще используется в этом смысле.
Типы магм
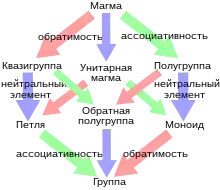
Как таковые магмы обычно не изучаются; вместо этого изучаются различные типы магм, отличающиеся дополнительно вводимыми аксиомами. Обычно изучаемые типы магм включают следующие:
- квазигруппа — непустая магма, в которой всегда возможно деление;
- петля или лупа — квазигруппа с нейтральным элементом;
- полугруппа — магма с ассоциативной операцией;
- моноид — полугруппа с нейтральным элементом;
- группа — моноид с обратным элементом или, то же что, ассоциативная петля (всегда являющаяся квазигруппой);
- абелева группа — группа с коммутативной операцией.
Морфизм магм
Морфизм магм — это функция , соотносящая магме магму , которая сохраняет бинарную операцию:
где и обозначают бинарные операции на и на соответственно.
Комбинаторика и скобки
Для общего, неассоциативного случая, операция магмы может быть многократно повторена. Для обозначения порядка используются скобки. Результирующая строка состоит из символов, обозначающих элементы магмы и сбалансированных скобок. Множество всех возможных строк сбалансированных скобок называется языком Дика. Общее число различных способов записи n применений оператора магмы определяется числом Каталана . Так например, , что эквивалентно утверждению, что и — единственно возможные способы определения порядка двукратного применения бинарной операции магмы.
Для упрощения записи и сокращения числа используемых скобок используется условное обозначение. Для того, чтобы обозначить более высокий приоритет у выполнения операции используют запись рядом. Например, если операция магмы «·», то xy·z — сокращённая запись (x · y) · z. Дальнейшие сокращения возможны за счёт использования пробелов. Например, записывая xy·z · wv вместо ((x · y) · z) · (w · v). Разумеется, для более сложных выражений отказ от использования скобок нежизнеспособен. Способом избежать использования скобок является префиксная запись, которая, однако, неинтуитивна.
См. также
Литература
- Куликов Л. Я. Алгебра и теория чисел. — М.: Высшая школа, 1979. — 559 с.
