Квантовая яма

Квантовая яма — узкая потенциальная яма, которая ограничивает возможность движения частиц с трех до двух измерений, тем самым заставляя их перемещаться в плоском слое. Является двумерной (англ. two-dimensional, 2D) системой. Квантово-размерные эффекты проявляют себя, когда ширина ямы становится сравнимой с длиной волны де Бройля частиц (обычно электронов или дырок), и приводят к появлению энергетических подзон размерного квантования.

Энергия $E$ частицы в яме может быть представлена как сумма $E_{z}+E_{xy}$ энергии движения в направлении квантования ( $z$ на рис.) и свободного движения в перпендикулярной плоскости ( $xy$ на рис.). При этом $E_{z}$ принимает только дискретные значения, равные энергии $E_{n}$ дна какой-то из подзон, а на $E_{xy}$ ограничений нет.

Квантовой ямой иногда называют систему с ограничением движения не только по одному, но и по двум или по трём декартовым координатам — с уточнением (по числу свободных направлений): «двумерная» (2D), «одномерная» (1D) или «нульмерная» (0D) яма. Но чаще в последних случаях используются термины «квантовый провод» (1D) и «квантовая точка» (0D).

Создание квантовых ям

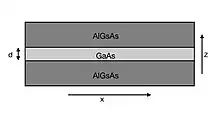
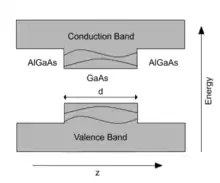
Пример сочетания материалов, при котором в среднем слое образуется яма и для электронов, и для дырок.

Зонная диаграмма структуры с кватновой ямой; схематично показан вид волновых функций.

Один из наиболее распространённых способов формирования квантовых ям в современных условиях — последовательное нанесение слоёв A—B—A полупроводниковых материалов, где материал B таков, что либо край его зоны проводимости лежит ниже края зоны проводимости материала A, либо край валентной зоны В лежит выше края валентной зоны А, либо и то и другое. Толщина слоя B обычно составляет несколько нанометров.

Оценка энергий подзон

Энергию дна каждой из подзон размерного квантования можно приблизительно оценить с помощью выражения:

E_{n}={\frac {\hbar ^{2}}{2m^{*}}}\left({\frac {\pi n}{d}}\right)^{2}

,

где $n$ — номер подзоны размерного квантования, $m^{*}$ — эффективная масса соответствующей квазичастицы, $d$ — ширина квантовой ямы. Формула справедлива только тогда, когда энергия меньше, чем глубина ямы.

Для очень глубокой ямы (в пределе — для прямоугольной ямы с бесконечными стенками) эта формула даёт точные значения энергий $E_{n}$ . На практике, хотя ямы нередко являются прямоугольными, высота их стенок конечна и составляет от долей эВ до нескольких эВ.

Если в яме находится достаточно большое число заряженных частиц, то они создают поле, искажающее профиль потенциала и значения энергий подзон. Для рассмотрения подобных ситуаций существует метод Хартри-Фока.

Некоторые значимые свойства

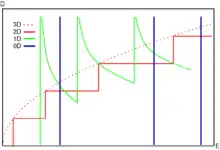
Плотность состояний как функция энергии в трёхмерных системах и в случаях пониженной размерности. Для ямы (2D) — сплошная красная линия.

Из-за квазидвумерной природы в пределах одной подзоны размерного квантования плотность состояний не зависит от энергии, но, когда значение энергии превышает энергию дна следующей подзоны, плотность состояний резко возрастает, в отличие от корневой зависимости в случае трехмерных электронов.

Квантовая яма может оставаться пустой, а может быть наполненной электронами или дырками. Добавляя донорную примесь, можно получить двумерный электронный газ, обладающий интересными свойствами при низкой температуре. Одним из таких свойств является квантовый эффект Холла, наблюдаемый в сильных магнитных полях. Добавление же акцепторной примеси приведет к получению двумерного дырочного газа.

Распределение заряда по координате $z$ зависит от вида волновых функций частиц в состояниях с энергиями $E_{n}$ , а именно:

\rho (z)=q\sum _{n}N_{s,n}|\psi _{n}(x)|^{2}

,

здесь $q$ — заряд электрона, $\psi _{n}(x)$ — волновая функция электрона (м^-1/2) в состоянии $E_{n}$ , а $N_{s,n}$ — двумерная концентрация электронов (м^-2) в данном состоянии. Последняя рассчитывается как

N_{s,n}={\frac {m^{*}kT}{\pi \hbar ^{2}}}\ln \left(1+\exp {\frac {E_{F}-E_{n}}{kT}}\right)

,

где $E_{F}$ — энергия Ферми, $k$ — постоянная Больцмана, $T$ — температура. Полная концентрация есть сумма $N_{s,n}$ по всем $n$ . Нередко оказывается, что заполнена только нижняя подзона, тогда $N_{s,n}\approx 0$ для $n>1$ . На границах ямы ( $z=0$ и $z=d$ ) плотность заряда обычно мала, а для ямы с бесконечными стенками она равна нулю.

Приборы с квантовыми ямами

Благодаря особенностям поведения 2D плотности состояний, задействование квантовых ям позволяет улучшить характеристики ряда оптических приборов. Структуры с квантовыми ямами широко используются в лазерных диодах, включая красные лазеры для DVD и лазерных указок, инфракрасных лазерах для оптических передатчиков и синих лазерах. Также используются в транзисторах с высокой подвижностью электронов используемых в малошумящей электронике. Инфракрасные фотодетекторы также основаны на применении квантовых ям[1].

Находят применение и более сложные структуры с ямами. Например, резонансно-туннельный диод использует квантовую яму между двумя барьерами для создания отрицательного дифференциального сопротивления.

См. также

Примечания

Бузанева, 1990, с. 147-202.

Литература

Thomas Engel, Philip Reid. Quantum Chemistry and Spectroscopy. — Pearson Education, 2006. — С. 73—75. — ISBN 0-8053-3843-8.
Бузанева Е. В. Микроструктуры интегральной электроники. — М.: Радио и связь, 1990. — 304 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_de75103f03c59345-1] Бузанева, 1990, с. 147-202.