Электронная теория металлов

Электронная теория металлов — раздел физики твёрдого тела, который изучает физические свойства металлов или металлического состояния вещества. В основном предметом исследования теории являются кристаллические вещества с металлическим типом проводимости[1]. В основе теории металлов лежит зонная теория твёрдых тел. Волновые функции электроны на внутренних орбиталях слабо перекрываются, что приводит к сильной локализации, а для внешних валентных электронов качественную картину энергетического спектра может дать модель почти своодных электронов.

Общие свойства

Электронные оболочки атомов составляющих кристаллическую решётку типичных металов сильно перекрываются, в результате чего нельзя указать у какого иона локализован тот или иной электрон валентной оболочки — они легко перетекают от одного иона к другому и, в этом случае, говорят, что электроны коллективизированы[1]. Ионы представляют собой ядра и электроны внутренних оболочек, которые сильно локализованы и электронов, которые делокализованные электроны внешних оболочек, которые свободно перемещаются по кристаллу. Именно свободные электроны отвечают за многие физические и, в особенности, транспортные свойства металлов[1]. Не смотря на то, что электроны сильно взаимодействуют с ионными остовами решётки и между собой, теорию металлов можно построить для невзаимодействующих электронов — теперь уже не обычных частиц, а квазичастиц, обладающих отличающимися физическими характеристиками и двигающихся в эффективном поле (среднее поле), которое включает в себя действие всех остальных электронов и ионов металла. Кристаллическая решётка должна обладать трансляционной симметрией, которая выражается в периодической зависимости многих физических свойств кристалла. Например, для потенциальной энергии кристалла можно записать[2]

$U({\textbf {r}}+{\textbf {a}}_{n})=U({\textbf {r}})\,,$

(Ур. 1.1)

где вектор ${\textbf {a}}_{n}$ — это произвольный период решётки, который представляется в виде суммы произведения тройки целых чисел и тройки базисных векторов

${\textbf {a}}_{n}=n_{1}{\textbf {a}}_{1}+n_{2}{\textbf {a}}_{2}+n_{3}{\textbf {a}}_{3}\,.$

(Ур. 1.2)

Стационароное уравнение Шрёдингера для трёхмерного кристалла записывается в виде

$-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi ({\textbf {r}})+U({\textbf {r}})\psi ({\textbf {r}})=\varepsilon \psi ({\textbf {r}})\,.$

(Ур. 1.3)

где $\hbar$ — редуцированная постоянная Планка, m — эффективная масса электрона, ε — энергия. Волновая функция удовлетворяет условию[3]

$\psi ({\textbf {r}}+{\textbf {a}}_{n})=e^{i{\textbf {p}}{\textbf {a}}_{n}/\hbar }\psi ({\textbf {r}})=e^{i{\textbf {p}}({\textbf {r}}+{\textbf {a}}_{n})/\hbar }u({\textbf {r}})\,,$

(Ур. 1.4)

которое выражает теорему Блоха. Здесь u — периодическая функция

u({\textbf {r}}+{\textbf {a}}_{n})=u({\textbf {r}})\,,

а ${\textbf {p}}/\hbar$ — некий векторный коэффициент, определённый с точностью до вектора обратной решётки K, который обладает свойством K a_n=2πm, где m — целое число. Эта величина называется волновым вектором, а p — квазиимпульсом[4].

Для уравнения Шрёдингера в кристалле задают также периодические граничные условия, которые определяют возможные значения для векторного параметра ${\textbf {p}}/\hbar$ . Например для параллепипеда (много больше, чем размер элементарной ячейки) со сторонами L_i, где индекс принимает значения x, y, z[3]

{\frac {p_{i}}{\hbar }}={\frac {2\pi n_{i}}{L_{i}}}\,,

где n_i — большие натуральные числа. Вектор p принимает дискретные значения, но разделены эти значения такими малыми интервалами Δp_i, что их рассмаривают как дифференциалы dp_i. Число состояний dN в элементе объёма d³p=dp_xdp_ydp_z равна

dN={\frac {V}{(2\pi \hbar )^{3}}}d^{3}{\textbf {p}}\,,

где V — объём кристалла, а выражение в правой части перед дифференциалом имеет смысл плотности состояний. Здесь не учитывается вырождение по спину. При двух возможных ориентациях спина к плотности состояний добавляется множитель двойка[5].

Зона Бриллюэна для гранецентрированной кубической решетки. Показаны линии и точки симметрии.

Для выбора области определения квазиимпульса в пространстве квазиимпульсов, чтобы не было квазиимпульсов отличающихся на вектора обратной решётки, удобно построить элементарную ячейку Вигнера — Зейца отображённую в обратное пространство, которая называется зоной Бриллюэна[6]. Энергия как функция квазиимпульса обладает симметрией относительно замены знака квазиимпульса

\varepsilon ({\textbf {p}})=\varepsilon (-{\textbf {p}})\,,

что следует из эрмитовости гамильтониана[5]. Часто решётки металлов обладают большой симметрией, что отражается на свойствах энергетичекого спектра[6]. Симметрия элементарной ячейки находит отражение в симметрии энергетического спектра. Например, на краях или в центре элементарной ячейки (гранецентрированные, объёмоцентрированные или кубические) расположены точки высокой симметрии, где энергия достигает экстремумов.

Приближение сильно связанных электронов

Для рассчёта зонной структуры металлов $\varepsilon ({\textbf {p}})$ применяются сложные численные методы. Однако, для качественно понимания поведения квазичастиц в металле можно рассмотреть электроны в периодическом потенциале кристалла (одномерном металле с периодом a) в приближении сильной связи. Стационарное уравнение Шрёдингера примет виде[7]

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=\varepsilon \psi (x)\,,$

(Ур. 2.1)

где потенциал равен

$V(x)=\sum _{n}U(x-na)\,.$

(Ур. 2.2)

Решения уравнения (2.1) можно представить в виде блоховских функций

$\psi _{p}(x)=e^{ipx/\hbar }u_{p}(x)$

(Ур. 2.3)

с собственными значениями ε(p). Эти функции используют для построения функций Ванье

$w_{n}(x)=N^{-1/2}\sum _{p}e^{-ipna/\hbar }\psi _{p}(x)\,,$

(Ур. 2.4)

где N — число атомов в кристалле, квазиимпульс ограничен первой зоной Бриллюэна $-\pi \hbar /a\leq p\leq \pi \hbar /a\,.$ Функция w_n локализована на n-ом атоме. Ванье функции формируют ортонормированный базис и блоховские функции можно выразить через функции Ванье (обратное преобразование)[7]

$\psi _{p}(x)=N^{-1/2}\sum _{n}e^{ipna/\hbar }w_{n}(x)\,.$

(Ур. 2.5)

Если подставить это выражение в уравнение Шрёдингера (2.1) можно использовать метод последовательных приближений для поиска энергий и волновых функций.

$\sum _{n}\left(-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}+U(x-na)\right)e^{ipna/\hbar }w_{n}(x)+\sum _{n}h(x)e^{ipna/\hbar }w_{n}(x)=\varepsilon (p)\sum _{n}e^{ipna/\hbar }w_{n}(x)\,,$

(Ур. 2.6)

где малый потенциал

$h(x)=V(x)-\sum _{n}U(x-na)\,.$

(Ур. 2.7)

В нулевом приближении можно использовать волновую функцию изолированного атома w⁽⁰⁾=φ(x), которому соответствует энергия ε₀. А для первого порядка получается следующее уравнение[8]

$\sum _{n}\left(-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}+U(x-na)-\varepsilon _{0}\right)w^{(1)}e^{ipna/\hbar }=(\varepsilon (p)-\varepsilon _{0})\sum _{n}e^{ipna/\hbar }w_{n}^{(0)}(x)-\sum _{n}h(x)e^{ipna/\hbar }w_{n}^{(0)}(x)\,.$

(Ур. 2.8)

Решение этого уравнения следует из условия ортогональности[9]

$\varepsilon (p)-\varepsilon _{0}={\frac {\sum _{n}h(n)e^{ipna/\hbar }}{\sum _{n}I(n)e^{ipna/\hbar }}}={\frac {\sum _{n}\int \phi ^{*}(x)h(x)\phi (x-na)dxe^{ipna/\hbar }}{\sum _{n}\int \phi ^{*}(x)\phi (x-na)dxe^{ipna/\hbar }}}=h(0)+2(h(1)-h(0)I(1))\cos(pa/\hbar )\,,$

(Ур. 2.9)

где коэффициент перед косинусом определяет ширину зоны, а сама энергия есть периодическая функция квазиимпульса с периодом $2\pi \hbar /a$ . В центре и на краях зоны Бриллюэна функция имеет экстремумы. Физическая картина представляется в виду уширения слабо перекрывающихся индивидуальных уровней изолированных атомов, что применимо для электронов на внутренних оболочках. В частности некоторые зоны переходных и редкоземельных металлов можно найти из трёхмерного обобщения рассмотренной одномерной задачи[10].

Приближение почти свободных электронов

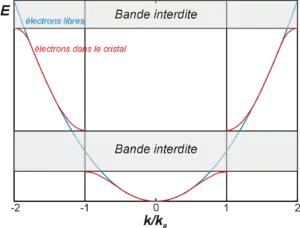
Зона Бриллюэна для одномерной решётки решетки. Показаны параболический закон дисперсии и запрешённые зоны.

Для почти свободных электронов, применима теория возмущений. Электронная волновая функция для параболического закона дисперсии с энергией $\varepsilon ^{(0)}=p^{2}/2m$ в одномерной системе размера L представляется в виде плоской волны для уравнения Шрёдингера Hψ=Eψ[10]

$\psi ^{(0)}={\frac {1}{L^{1/2}}}e^{ipx/\hbar }\,.$

(Ур. 3.1)

Периодический потенциал удобно разложить в ряд Фурье по векторам обратной решётки

$U(x)=\sum _{n}U_{n}e^{2\pi inx/a}$

(Ур. 3.2)

Матричные элементы для потенциала U(p,p')=<p'|U(x)|p> определяется стандартным способом

$U(p,p')=L^{-1}\int U(x)e^{-i(p-p')x/\hbar }dx=U_{n}\,.$

(Ур. 3.3)

Первый порядок теории возмущений даёт постоянный сдвиг нулевой энергии $\varepsilon ^{(1)}=U(p,p)=U_{0}$ , а для второго порядка поправка принимает виде

$\varepsilon ^{(2)}(p)=\sum _{n\neq 0}{\frac {|U_{n}|^{2}}{\varepsilon ^{(0)}(p)-\varepsilon ^{(0)}(p-2\pi n\hbar /a)}}\,.$

(Ур. 3.4)

Теория возмущений теряет применимость в точках на краю зон Бриллюэна из-за вырождения по квазиимпульсу, поэтому волновую функцию ψ представляют в виду суперпозиции двух волновых функций ψ=A₁ψ₁+A₂ψ₂ с неизвестными коэффициентати и применяют теорию возмущений для вырожденных уровней, решая секулярное уравнение. Энергия на краях зон Бриллюэна имеет вид

$\varepsilon ={\frac {1}{2}}\left({\frac {p^{2}}{2m}}+{\frac {p'^{2}}{2m}}\right)\pm \left[{\frac {1}{4}}\left({\frac {p^{2}}{2m}}-{\frac {p'^{2}}{2m}}\right)^{2}+|U_{n}|^{2}\right]^{1/2}\,,$

(Ур. 3.5)

со скачком равным $2|U_{n}|$ при $p=\pm \pi n\hbar /a$ [11].

Электроны в металле

Свойства свободных электронов и электронов в металле[12]
	Свободный электрон	Комментарии	Электрон проводимости	Комментарии
Стационарная волновая функция	$\psi =Ae^{i{\textbf {pr}}/\hbar }$	A — константа	$\psi _{s}=u_{s}({\textbf {r}})e^{i{\textbf {pr}}/\hbar }\,,$ $U_{s}({\textbf {r}})=U_{s}({\textbf {r}}+{\textbf {a}})$	теорема Блоха
Энергия	$E={\frac {{\textbf {p}}^{2}}{2m}}$		$E_{s}({\textbf {p}})=E_{s}({\textbf {p}}+2\pi \hbar {\textbf {b}})$	b — вектор обратной решётки
Изоэнергетическая поверхность	$p^{2}=2mE$	сфера	$E_{s}({\textbf {p}})=const$	периодическая поверхность
Скорость	${\textbf {v}}={\frac {\textbf {p}}{m_{0}}}$		${\textbf {v}}({\textbf {p}})={\frac {\partial E}{\partial {\textbf {p}}}}$
Масса	$m_{0}$	масса покоя электрона	$\left({\frac {1}{m}}\right)_{ik}={\frac {\partial ^{2}E}{\partial i\partial k}}$	тензор обратных эффективных масс
Циклотронная масса	$m_{0}$	масса покоя электрона	${\textbf {H}}=(0,0,H_{z})\,,$ $m={\frac {1}{2\pi }}{\frac {\partial S(E,p_{z})}{\partial E}}$	S площадь сечения изоэнергетической поверхности при p_z=const
Законы сохранения при столкновениях двух электронов	$E_{1}+E_{2}=E_{1}'+E_{2}'\,,$ ${\textbf {p}}_{1}+{\textbf {p}}_{2}={\textbf {p}}_{1}'+{\textbf {p}}_{2}'$	Закон сохранения энергии и импульса	$E_{1}+E_{2}=E_{1}'+E_{2}'\,,$ ${\textbf {p}}_{1}+{\textbf {p}}_{2}={\textbf {p}}_{1}'+{\textbf {p}}_{2}'+2\pi \hbar {\textbf {b}}$	квазиимпульс сохраняется с точностью до вектора обратной решётки
Плотность состояний	$g(E)={\frac {V}{\pi ^{2}\hbar ^{3}}}{\sqrt {2m_{0}^{3}E}}$		$g(E)={\frac {2V}{(2\pi \hbar )^{3}}}\oint {\frac {df}{{\textbf {v}}({\textbf {p}})}}$	df — элемент площади изоэнергетической поверхности
Энергия Ферми	$E_{F}={\frac {(3\pi ^{2}n)^{2/3}}{2m_{0}}}$	n — концентрация вырожденного газа	${\frac {\Omega _{s}(E_{F})}{4\pi ^{3}\hbar ^{3}}}=n_{s}$	Ω_s — объём листа поверхности Ферми в пространстве квазиимпульсов при концентрации n_s

Теория Ферми-жидкости

Электроны в металле взаимодействуют друг с другом и с ионами решётки. Теорию взаимодействия электронов в вырожденном электронном газе можно построить с использованием концепции Ландау о ферми-жидкости[13]. Для идеального Ферми-газа функция распределения описывается известной формулой

$f={\frac {1}{e^{(\varepsilon -\mu )/T}+1}}\,,$

(Ур. 4.1)

где ε=p²/2m — энергия электрона, μ — химический потенциал, T — температура. При нулевой температуре химический потенциал μ(0) разделяет заполненные и незаполненные уровни и называется уровнем Ферми[14]. С этим уровнем Ферми связан импульс Ферми, который задаёт радиус сферы Ферми для металлов с параболическим и изотропным законом дисперсии

$p_{0}=\hbar (3\pi ^{2}N/V)^{1/3}\,,$

(Ур. 4.2)

где V — объём, N — число частиц. При конечной температуре в металле появляются возбуждённые частицы — состояния вне сферы Ферми, и античастицы — с энергией меньшей уровня Ферми. Для таких квазичастичных состояний энергию можно отсчитывать от уровня Ферми и для малых отклонений можно записать[15]

$\xi _{p,a}=\pm \left({\frac {p^{2}}{2m}}-{\frac {p_{0}^{2}}{2m}}\right)\approx \pm v(p-p_{0})\,,$

(Ур. 4.3)

где v=p₀/m — скорость на сферы Ферми. Индексы p и a относятся к частицам и античастицам. Концепция квазичастиц применима в случае, когда T<<μ(0)[16].

Примечания

Абрикосов, 1987, с. 9.
Абрикосов, 1987, с. 10.
Абрикосов, 1987, с. 12.
Абрикосов, 1987, с. 11.
Абрикосов, 1987, с. 13.
Абрикосов, 1987, с. 14.
Абрикосов, 1987, с. 15.
Абрикосов, 1987, с. 16.
Абрикосов, 1987, с. 17.
Абрикосов, 1987, с. 18.
Абрикосов, 1987, с. 19.
В. С. Крапошин. Металлы // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
Абрикосов, 1987, с. 21.
Абрикосов, 1987, с. 24.
Абрикосов, 1987, с. 25.
Абрикосов, 1987, с. 27.

Литература

Абрикосов А. А. Основы теории металлов (рус.). — М.: Наука, 1987. — 520 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_3871d0f043bf51ad-1] Абрикосов, 1987, с. 9.

[_a8b7ad431e17bb6f-2] Абрикосов, 1987, с. 10.

[_a8b7ad431e17bb6d-3] Абрикосов, 1987, с. 12.

[_a8b7ad431e17bb6e-4] Абрикосов, 1987, с. 11.

[_a8b7ad431e17bb6c-5] Абрикосов, 1987, с. 13.

[_a8b7ad431e17bb6b-6] Абрикосов, 1987, с. 14.

[_a8b7ad431e17bb6a-7] Абрикосов, 1987, с. 15.

[_a8b7ad431e17bb69-8] Абрикосов, 1987, с. 16.

[_a8b7ad431e17bb68-9] Абрикосов, 1987, с. 17.

[_a8b7ad431e17bb67-10] Абрикосов, 1987, с. 18.

[_a8b7ad431e17bb66-11] Абрикосов, 1987, с. 19.

[:1-12] В. С. Крапошин. Металлы // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

[_a8b7ae431e17bd23-13] Абрикосов, 1987, с. 21.

[_a8b7ae431e17bd26-14] Абрикосов, 1987, с. 24.

[_a8b7ae431e17bd27-15] Абрикосов, 1987, с. 25.

[_a8b7ae431e17bd25-16] Абрикосов, 1987, с. 27.