Филогенетическое дерево
Филогенетическое дерево (эволюционное дерево, дерево жизни) — дерево, отражающее эволюционные взаимосвязи между различными видами или другими сущностями, имеющими общего предка.
Вершины филогенетического дерева делятся на три класса: листья, узлы и (максимум один) корень. Листья — это конечные вершины, то есть те, в которые входят ровно по одному ребру; каждый лист отображает некоторый вид живых организмов (или иной объект, подверженный эволюции, например, домен белка). Каждый узел представляет эволюционное событие: разделение предкового вида на два или более, которые в дальнейшем эволюционировали независимо. Корень представляет общего предка всех рассматриваемых объектов. Ребра филогенетического дерева принято называть «ветвями».
Идея «дерева» появилась в ранних взглядах на жизнь, как на процесс развития от простых форм к сложным. Современные эволюционные биологи продолжают использовать деревья для иллюстрации эволюции, так как они наглядно показывают взаимосвязи между живыми организмами.
Типы филогенетических деревьев
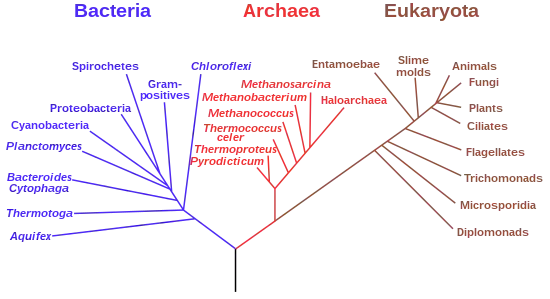
Укоренённое дерево — дерево, содержащее выделенную вершину — корень. Укоренённое дерево можно считать ориентированным графом, поскольку на нём имеется естественная ориентация — от корня к листьям. Каждый узел укоренённого дерева отвечает последнему общему предку нижележащих листьев дерева. На иллюстрации показано укоренённое филогенетическое дерево, окрашенное в соответствии с трёхдоменной системой живых организмов[2].
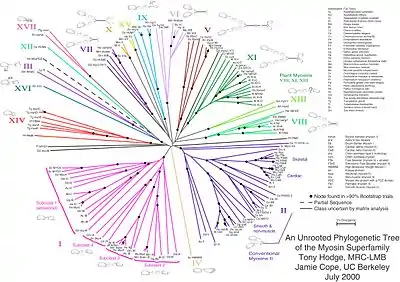
Неукоренённое дерево не содержит корня и отражает связь листьев без предполагаемого положения общего предка. Необходимость рассматривать неукоренённые деревья возникает из-за того, что часто связи между узлами восстановить легче, чем направление эволюции. На иллюстрации показано неукоренённое филогенетическое дерево[3]. Наиболее достоверным методом для превращения неукоренённого дерева в укоренённое (для этого надо либо объявить корнем один из узлов, либо разбить одну из ветвей на две, выходящие из корня) является использование «внешней группы» видов — достаточно близких к интересующему нас набору видов (для достоверного восстановления топологии дерева для объединённого множества видов), но в то же время заведомо являющихся отдельной группой. Иногда положение корня можно угадать, исходя из каких-либо дополнительных знаний о природе изучаемых объектов (видов, белков, и т. д.)
Укоренённое и неукоренённое филогенетическое дерево может быть бифуркационным или небифуркационным, а также маркированным или немаркированным. В бифуркационном дереве к каждому узлу подходят ровно три ветви (в случае укоренённого дерева — одна входящая ветвь и две исходящие). Таким образом, бифуркационное дерево предполагает, что все эволюционные события состояли в происхождении от предкового объекта ровно двух потомков. К узлу небифуркационного дерева могут подходить четыре и более ветви. Маркированное дерево содержит названия листьев, тогда как немаркированное просто отражает топологию.
Дендрограмма — общий термин, обозначающий схематическое представление филогенетического дерева.
Кладограмма — филогенетическое дерево, не содержащее информации о длинах ветвей.
Филограмма (или фенограмма) — филогенетическое дерево, содержащее информацию о длинах ветвей; эти длины представляют изменение некой характеристики, например, число мутаций в каком-либо гене.
Хронограмма — филограмма, длины ветвей в которой представляют эволюционное время.
Построение филогенетических деревьев
В наше время филогенетические деревья, как правило, реконструируются по последовательностям белков или нуклеиновых кислот (ДНК или РНК) (см. Молекулярная филогенетика). Деревья строятся по произвольному числу входных последовательностей с использованием специальных вычислительных (филогенетических) алгоритмов. Наиболее достоверной мерой соответствия данного набора (выровненных) последовательностей данной топологии дерева считается мера (критерий), основанная на принципе наибольшего правдоподобия. Нередко используется также принцип Байеса, хотя его применимость спорна[4]. Вероятностные критерии (наибольшее правдоподобие и байесовские) требуют много машинного времени для своего вычисления. Другие критерии — так называемая «максимальная экономия» (maximum parsimony), а также несколько критериев, основанных на предварительном вычислении расстояний между входными последовательностями — вычисляются быстрее. Имеются результаты[5], показывающие, что некоторые критерии, основанные на вычислении расстояний, не только быстрее вычисляются, но и более достоверны, чем критерии, основанные на наибольшем правдоподобии.
Для любого критерия встаёт задача нахождения оптимального (для данной меры) дерева. Время точного решения этой задачи растёт факториально (много быстрее, чем экспоненциально!) с ростом числа входных последовательностей, поэтому для нахождения дерева, в достаточной мере удовлетворяющего входным данным, используются эвристический поиск и методы оптимизации. Кроме того, популярны такие алгоритмы, как метод присоединения соседей, которые вообще не используют перебор топологий и вычисление какого-либо критерия, а сразу строят дерево, которое при хорошем качестве входных данных достаточно достоверно.
Методы построения деревьев могут быть оценены по нескольким основным показателям[6]:
- эффективность (сколько времени и памяти требуются для вычислений)
- полезность (есть ли польза от полученных данных или информация бесполезна)
- воспроизводимость (будут ли повторные ответы такими же, если каждый раз даются разные данные для той же проблемной модели)
- устойчивость к ошибкам (справляется ли с неточностями в предпосылках рассматриваемой модели)
- выдача предупреждений (будет ли предупреждать нас, когда неправильно используется, то есть предпосылки неверные)
Кроме того, методы можно разделить на предполагающие и не предполагающие справедливость гипотезы «молекулярных часов» (то есть одинаковой скорости изменений для всех предковых последовательностей, см. нейтральная теория молекулярной эволюции). Первая группа методов строит укоренённые деревья, вторая — как правило, неукоренённые. Чаще всего предполагать «молекулярные часы» нет достаточных оснований, и поэтому большинство компьютерных программ филогенетического анализа по умолчанию выдают неукоренённые деревья.
Методы реконструкции филогенетических деревьев применяются не только биологами, но и математиками и даже филологами[7]. Деревья можно строить, используя Т-теорию[8].
Среди бесплатных пакетов филогенетического анализа большим набором реализованных алгоритмов выделяется PHYLIP, среди платных — PAUP. Пакет SeaView, с одной стороны, удобен и прост в использовании, а с другой — обладает функционалом, достаточным для подготовки научной публикации. Для редактирования и визуализации готовых деревьев наиболее часто используются программы FigTree, Archaeopterix, iTOL, MEGA; последняя включает также реализацию основных алгоритмов реконструкции деревьев на основе выравненных биологических последовательностей. На русском языке доступна программа UGENE, распространяющаяся по свободной лицензии и включающая в себя построение и визуализацию деревьев.
Ограничения использования филогенетических деревьев
Хотя филогенетические деревья, построенные на основе последовательностей генов или всего генома особей различных видов, могут дать представление об эволюции, у них есть серьёзные ограничения. Филогенетические деревья не обязательно (и вероятно никогда) не дают полного и абсолютно правильного описания эволюционной истории. Данные, на которых основана реконструкция дерева, всегда отражают реальную эволюционную историю с некоторой погрешностью. Из-за этого дерево, построенное на основе ограниченных данных (например, последовательности единственного гена или белка), требует скептического отношения к себе, потому что дерево, построенное на основе другого независимого источника данных, нередко будет отличаться от первого.
Горизонтальный перенос генов, а также гибридизация между видами затрудняют использование деревьев для описания эволюции. В случаях, когда подобные эволюционные события сыграли большую роль в эволюции изучаемой группы, предлагается использовать более сложные методы описания, например филогенетические сети.
Как правило, реконструкция филогенетического дерева представляет собой оценку филогении особенностей (например, эволюционной истории какого-либо отдельного гена), а не филогении организмов, из которых были отобраны эти особенности, хотя в идеале обе филогении должны быть близки друг к другу.
Следует также скептически относиться к включению в дерево вымерших видов, информация о которых полностью или частично основана на последовательностях ДНК. Хотя небольшие фрагменты «древней ДНК» сохраняются дольше 100 000 лет, но, за исключением некоторых особых случаев, длина таких фрагментов недостаточна для использования в филогенетическом анализе.
В некоторых организмах эндосимбионты могут иметь эволюционную историю, отличную от истории хозяина.
См. также
Примечания
- Hodge T. & Cope M. J. T. V. 2000. A myosin family tree. Journal of Cell Science, 113:3353–3354.
- Woese C. R. 1998. The universal ancestor. Proceedings of the National Academy of Sciences, 95:6854–6859.
- Maher B. A. 2002. Uprooting the Tree of Life. The Scientist, 16:18; subscription only
- Felsenstein J. 2004. Inferring Phylogenies Sinauer Associates: Sunderland, MA.
- Gonnet G. H. 2012. Surprising results on phylogenetic tree building methods based on molecular sequences. BMC Bioinformatics, 13:148
- Penny D., Hendy M. D. & Steel M. A. 1992. Progress with methods for constructing evolutionary trees. Trends in Ecology and Evolution, 7:73–79.
- Barbrook A. C., Blake N., Robinson P. 1998. The phylogeny of Canterbury Tales, Nature, 394
- Dress A., Huber K. T., and Moulton V. 2001. Metric Spaces in Pure and Applied Mathematics. Documenta Mathematica, LSU 2001: 121—139
Ссылки
Изображения в интернете
- Эволюционное дерево гоминид — предков человека (на основании палеоантропологических данных)
- Exploring the Entire Tree of Life. Lifemap. Дата обращения: 2 января 2017.
Общее описание
- Филогенетический анализ семейства белков-гомологов (Дата обращения: 7 ноября 2009)
- PhyloCode
- A Multiple Alignment of 139 Myosin Sequences and a Phylogenetic Tree (англ.) (Дата обращения: 7 ноября 2009)
- Веб-проект построения «дерева жизни» (англ.) (Дата обращения: 7 ноября 2009)
- Семейство филогенетических деревьев эволюции динозавров (англ.) (Дата обращения: 7 ноября 2009)