Теорема Тейлора

Точная формулировка большинства базовых версий теоремы такова.

Теорема Тейлора[1] Пусть k ≥ 1 является целым, и пусть функция f : R → R является k раз дифференцируемой в точке a ∈ R. Тогда существует функция h_k : R → R такая, что

${\displaystyle f(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-a)^{k},\qquad \lim _{x\to a}h_{k}(x)=0.}$

Многочлен, возникающий в теореме Тейлора, является многочленом Тейлора k-го порядка

${\displaystyle P_{k}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}}$

функции f в точке a.

Теорема Тейлора описывает асимптотическое поведение остаточного члена

${\displaystyle \ R_{k}(x)=f(x)-P_{k}(x),}$

который является ошибкой при нахождении приближения функции f с помощью многочленов Тейлора. Используя «O» большое и «o» малое теорему Тейлора можно сформулировать так

${\displaystyle R_{k}(x)=o(|x-a|^{k}),\qquad x\to a.}$

Существует несколько точных формул для остаточного члена R_k многочлена Тейлора, наиболее общая из которых следующая.

Остаток в форме среднего значения. Пусть функция f : R → R является k+1 раз дифференцируемой на интервале ${\displaystyle (a,x)}$ и непрерывной на отрезке ${\displaystyle [a,x]}$. Тогда

${\displaystyle \exists \,\xi _{L}\in (a,x):R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}.}$

Это остаточный член в форме Лагранжа[2]. При тех же условиях

${\displaystyle \exists \,\xi _{C}\in (a,x):R_{k}(x)={\frac {f^{(k+1)}(\xi _{C})}{k!}}(x-\xi _{C})^{k}(x-a).}$

Это остаточный член в форме Коши[3].

Эти уточнения теоремы Тейлора обычно выводятся с помощью формулы конечных приращений.

Можно так же найти и другие выражения для остатка. Например, если G(t) является непрерывной на закрытом интервале и дифференцируемой с нестремящейся к нулю производной на открытом интервале между a и x, то

${\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G(x)-G(a)}{G'(\xi )}}}$

для некоторого числа ξ между a и x. Эта версия охватывает формы Лагранжа и Коши как частные случаи, и выводится с помощью теоремы Коши о среднем значении (расширенной версии теоремы Лагранжа о среднем значении).

Запись формулы для остатка в интегральной форме является более общей, чем предыдущие формулы, и требует понимания интегральной теории Лебега. Однако она сохраняется также для интеграла Римана при условии, что производная порядка (k+1) от f является непрерывной на закрытом интервале [a,x].

Интегральная форма[4] записи формулы для остатка Пусть f^(k) является абсолютно непрерывной на закрытом интервале между a и x. Тогда

${\displaystyle R_{k}(x)=\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt.}$

Вследствие абсолютной непрерывности f^(k) на закрытом интервале между a и x, её производная f^(k+1) существует как L¹-функция, и это следствие может быть получено с помощью формальных вычислений с использованием теоремы Ньютона — Лейбница и интегрирования по частям.

На практике часто бывает полезно численно оценить величину остаточного члена приближения Тейлора.

Будем считать, что f является (k+1)-раз непрерывно дифференцируемой на интервале I, содержащем a. Будем считать, что существуют действительные постоянные числа q и Q такие, что

${\displaystyle q\leq f^{(k+1)}(x)\leq Q}$

на всём протяжении I. Тогда остаточный член удовлетворяет неравенству[5]

${\displaystyle q{\frac {(x-a)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq Q{\frac {(x-a)^{k+1}}{(k+1)!}},}$

если x > a, и схожая оценка, если x < a. Это простое следствие из формулы остатка в Лагранжевой форме. В частности, если

${\displaystyle |f^{(k+1)}(x)|\leq M}$

на интервале I = (a−r,a+r) с некоторым r>0, то

${\displaystyle |R_{k}(x)|\leq M{\frac {|x-a|^{k+1}}{(k+1)!}}\leq M{\frac {r^{k+1}}{(k+1)!}}}$

для всех x∈(a−r,a+r). Второе неравенство называется равномерной оценкой, потому что она сохраняет равномерность для всех x на интервале (a−r,a+r).

Приближение e^x (голубой) с помощью многочленов Тейлора P_k порядка k=1,…,7 с центром в точке x=0 (красный).

Допустим, мы хотим найти приближение функции f(x) = e^x на интервале [−1,1] и убедиться, что ошибка не превышает значения 10⁻⁵. В этом примере считаем, что нам известны следующие свойства экспоненциальной функции:

${\displaystyle (*)\qquad e^{0}=1,\qquad {\frac {d}{dx}}e^{x}=e^{x},\qquad e^{x}>0,\qquad x\in \mathbb {R} .}$

Из этих свойств следует, что f^(k)(x) = e^x для всех k, и в частности, f^(k)(0) = 1. Отсюда следует, что многочлен Тейлора k-го порядка функции f в точке 0 и его остаточного члена в форме Лагранжа даётся формулой

${\displaystyle P_{k}(x)=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\qquad R_{k}(x)={\frac {e^{\xi }}{(k+1)!}}x^{k+1},}$

где ξ — это некоторое число между 0 и x. Поскольку e^x возрастает согласно (*), мы можем использовать e^x ≤ 1 для x ∈ [−1, 0], чтобы оценить остаток на подынтервале [−1, 0]. Для нахождения верхней границы значения остатка на интервале [0,1], можем использовать свойство e^ξ<<e^x для 0<ξ<x, чтобы оценить

${\displaystyle e^{x}=1+x+{\frac {e^{\xi }}{2}}x^{2}<1+x+{\frac {e^{x}}{2}}x^{2},\qquad 0<x\leq 1}$

используя многочлен Тейлора второго порядка. Выражая из этого неравенства e^x, приходим к выводу, что

${\displaystyle e^{x}\leq {\frac {1+x}{1-{\frac {x^{2}}{2}}}}=2{\frac {1+x}{2-x^{2}}}\leq 4,\qquad 0\leq x\leq 1}$

приняв, что числитель принимает максимальное из всех своих возможных значений, а знаменатель принимает минимальное из всех своих возможных значений. Используя эти оценки значений e^x, мы видим, что

${\displaystyle |R_{k}(x)|\leq {\frac {4|x|^{k+1}}{(k+1)!}}\leq {\frac {4}{(k+1)!}},\qquad -1\leq x\leq 1,}$

и требуемая точность определённо достигается в том случае, когда

${\displaystyle {\frac {4}{(k+1)!}}<10^{-5}\quad \Leftrightarrow \quad 4\cdot 10^{5}<(k+1)!\quad \Leftrightarrow \quad k\geq 7.}$

(где факториал 7!=5 040 и 8!=40 320.) В конечном счёте, теорема Тейлора приводит к приближению

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\ldots +{\frac {x^{7}}{7!}}+R_{7}(x),\qquad |R_{7}(x)|<10^{-5},\qquad -1\leq x\leq 1.}$

Отметим, что это приближение позволяет вычислить значение e≈2.71828 с точностью до пятого знака после запятой.

Пусть ${\displaystyle I\subset \mathbb {R} }$ является открытым интервалом. По определению, функция ${\displaystyle f\,:\,I\rightarrow \mathbb {R} }$ является вещественной аналитической, если она на данном участке определена сходимостью степенного ряда. Это означает, что для каждого ${\displaystyle a\in I}$ существует некоторое r > 0 и последовательность коэффициентов c_k ∈ R такая, что (a − r, a + r) ⊂ I и

${\displaystyle f(x)=\sum _{k=0}^{\infty }c_{k}(x-a)^{k}=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+\cdots ,\qquad |x-a|<r.}$

В общем, радиус сходимости степенного ряда может быть вычислен по формуле Коши–Адамара

${\displaystyle {\frac {1}{R}}=\limsup _{k\to \infty }|c_{k}|^{\frac {1}{k}}.}$

Этот результат основан на сравнении с бесконечно убывающей геометрической прогрессией, и тот же самый метод показывает, что если степенной ряд, разложенный по a, сходится для некоторого b∈R, он должен сходиться равномерно на закрытом интервале [a − r_b, a + r_b], где r_b = |b − a|. Здесь мы только рассмотрели сходимость степенного ряда, и не исключено, что область (a − R,a + R) расширяется за пределы области определения I функции f.

Многочлен Тейлора от вещественной аналитической функции f в точке a

${\displaystyle P_{k}(x)=\sum _{j=0}^{k}c_{j}(x-a)^{j},\qquad c_{j}={\frac {f^{(j)}(a)}{j!}}}$

является простым усечением определённого на некотором интервале соответствующего степенного ряда этой функции, и остаточный член на данном интервале даётся аналитической функцией

${\displaystyle R_{k}(x)=\sum _{j=k+1}^{\infty }c_{j}(x-a)^{j}=(x-a)^{k}h_{k}(x),\qquad |x-a|<r.}$

Здесь функция

${\displaystyle h_{k}:(a-r,a+r)\to \mathbb {R}$ ;\qquad h_{k}(x)=(x-a)\sum _{j=0}^{\infty }c_{k+1+j}(x-a)^{j}}

также является аналитической, поскольку её степенной ряд имеет тот же радиус сходимости, что и исходный ряд. При условии, что [a − r, a + r] ⊂ I и r < R, все эти ряды сходятся равномерно на интервале (a − r, a + r). Конечно, в случае аналитических функций можно оценить остаточный член R_k(x) путём «обрезания» последовательности производных f′(a) в центре приближения, но при использовании комплексного анализа появляются и другие возможности, которые описаны ниже.

Существует разногласие между многочленами Тейлора дифференцируемых функций и рядами Тейлора аналитических функций. Можно рассматривать (справедливо) ряд Тейлора

${\displaystyle f(x)\approx \sum _{k=0}^{\infty }c_{k}(x-a)^{k}=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+\ldots }$

бесконечное число раз дифференцируемой функции f:R→R как её «многочлен Тейлора бесконечно большого порядка» в точке a. Теперь оценка остатка многочлена Тейлора подразумевает, что для любого порядка k и для любого r>0 существует постоянная M_k,r>0 такая, что

${\displaystyle (*)\quad |R_{k}(x)|\leq M_{k,r}{\frac {|x-a|^{k+1}}{(k+1)!}}}$

для каждого x∈(a-r, a+r). Иногда эти постоянные могут быть выбраны таким образом, что M_k,r → 0, когда k → ∞ и r остаётся неизменной. Тогда ряд Тейлора функции f сходится равномерно к некоторой аналитической функции

${\displaystyle T_{f}:(a-r,a+r)\to \mathbb {R}$ ;\qquad T_{f}(x)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.}

Тут важно упомянуть тонкий момент. Возможна ситуация, когда бесконечное число раз дифференцируемая функция f имеет ряд Тейлора в точке a, который сходится в некоторой открытой окрестности точки a, но предельная функция T_f отличается от f. Важным примером этого феномена является такой

${\displaystyle f:\mathbb {R} \to \mathbb {R}$ ;\qquad f(x)={\begin{cases}e^{-{\frac {1}{x^{2}}}}&,x>0,\\0&,x\leq 0.\end{cases}}}

Используя цепное правило можно показать индуктивно, что для любого порядка k,

${\displaystyle f^{(k)}(x)={\begin{cases}{\frac {p_{k}(x)}{x^{3k}}}e^{-{\frac {1}{x^{2}}}}&,x>0\\0&,x\leq 0\end{cases}}}$

для некоторого многочлена p_k. Функция ${\displaystyle e^{-{\frac {1}{x^{2}}}}}$ стремится к нулю быстрее, чем любой полином, по мере того как x → 0, тогда f является бесконечное число раз дифференцируемой и f^(k)(0) = 0 для каждого положительного целого k. Теперь оценки для остатка многочлена Тейлора функции f показывают, что ряд Тейлора сходится равномерно к нулевой функции на всей действительной числовой оси. Не будет ошибки в следующих утверждениях:

• Ряд Тейлора функции f сходится равномерно к нулевой функции T_f(x)=0.
• Нулевая функция является аналитической, и каждый коэффициент её ряда Тейлора равен нулю.
• Функция f является бесконечное число раз дифференцируемой, но не аналитической.
• Для любого k∈N и r>0 существует M_{k, r}>0 такое, что остаточный член многочлена Тейлора k-го порядка функции f удовлетворяет условию (*).

Теорема Тейлора обобщает функции ${\displaystyle f:\mathbb {C} \to \mathbb {C} }$, которые являются комплексно дифференцируемыми на открытом подмножестве U ⊂ C комплексной плоскости. Однако её полезность снижена другими теоремами комплексного анализа, а именно: более полные версии подобных результатов могут быть выведены для комплексно дифференцируемых функций f : U → C с использованием интегральной формулы Коши как показано ниже.

Пусть r > 0 такое, что замкнутый круг B(z, r) ∪ S(z, r) содержится в U. Тогда интегральная формула Коши с положительной параметризацией γ(t)=re^it окружности S(z, r) с t ∈ [0,2π] даёт

${\displaystyle f(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-z}}dw,\quad f'(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-z)^{2}}}dw,\quad \ldots ,\quad f^{(k)}(z)={\frac {k!}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-z)^{k+1}}}dw.}$

Здесь все подынтегральные выражения являются непрерывными на окружности S(z, r), что обосновывает дифференцирование под знаком интеграла. В частности, если f является один раз комплексно дифференцируемой на открытом множестве U, то она фактически бесконечное число раз комплексно дифференцируема на U. Имеем оценку Коши[6]

${\displaystyle |f^{(k)}(z)|\leq {\frac {k!}{2\pi }}\int _{\gamma }{\frac {M_{r}}{|w-z|^{k+1}}}dw={\frac {k!M_{r}}{r^{k}}},\qquad M_{r}=\max _{|w-c|=r}|f(w)|}$

для любого z ∈ U и r > 0 такой, что B(z, r) ∪ S(c, r) ⊂ U. Эти оценки подразумевают, что комплексный ряд Тейлора

${\displaystyle f(z)\approx \sum _{k=0}^{\infty }{\frac {f^{(k)}(c)}{k!}}(z-c)^{k}}$

функции f сходится равномерно в любом круге B(c, r) ⊂ U с S(c, r) ⊂ U в некоторой функции T_f. Кроме того, используя формулу интегрирования по контуру для производных f^(k)(c),

${\displaystyle {\begin{aligned}T_{f}(z)=\ &\sum _{k=0}^{\infty }{\frac {(z-c)^{k}}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-c)^{k+1}}}dw={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-c}}\sum _{k=0}^{\infty }{\Big (}{\frac {z-c}{w-c}}{\Big )}^{k}dw\\=\ &{\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-c}}{\Big (}{\frac {1}{1-{\frac {z-c}{w-c}}}}{\Big )}dw={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-z}}dw=f(z),\end{aligned}}}$

таким образом, любая комплексно дифференцируемая функция f на открытом множестве U ⊂ C является комплексно аналитической. Всё то, что было написано выше для вещественных аналитических функций справедливо также и для комплексных аналитических функций, где открытый интервал I заменён на открытое подмножество U ∈ C и a-центрированные интервалы (a − r, a + r) заменена на c-центрированные круги B(c, r). В частности, разложение Тейлора сохраняется в виде

${\displaystyle f(z)=P_{k}(z)+R_{k}(z),\qquad P_{k}(z)=\sum _{j=0}^{k}{\frac {f^{(k)}(c)}{k!}}(z-c)^{k},}$

где остаточный член R_k является комплексно аналитическим. При рассмотрении рядов Тейлора методы комплексного анализа позволяют получить несколько более мощные результаты. Например, используя интегральную формулу для любого положительно ориентированную жорданову кривую γ которая параметризирует границу ∂W ⊂ U области W ⊂ U, можно получить выражение для производных f^(j)(c) как показано выше, и слегка изменив расчёты для T_f(z) = f(z), прийти к точной формуле

${\displaystyle R_{k}(z)=\sum _{j=k+1}^{\infty }{\frac {(z-c)^{j}}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-c)^{j+1}}}dw={\frac {(z-c)^{k+1}}{2\pi i}}\int _{\gamma }{\frac {f(w)dw}{(w-c)^{k+1}(w-z)}},\qquad z\in W.}$

Важная особенность здесь состоит в том, что качество приближения с помощью многочлена Тейлора в области W ⊂ U является мажорируемым значениями функции f на границе ∂W ⊂ U. Так же, применяя оценки Коши к выражению остатка Ряда, получаем равномерные оценки

${\displaystyle |R_{k}(z)|\leq \sum _{j=k+1}^{\infty }{\frac {M_{r}|z-c|^{j}}{r^{j}}}={\frac {M_{r}}{r^{k+1}}}{\frac {|z-c|^{k+1}}{1-{\frac {|z-c|}{r}}}}\leq {\frac {M_{r}\beta ^{k+1}}{1-\beta }},\qquad {\frac {|z-c|}{r}}\leq \beta <1.}$

График комплексной функции f(z) = 1/(1 + z²). Модуль показан высотой подъёма и аргумент показан цветом: циан=0, синий=π/3, фиолетовый=2π/3, красный=π, жёлтый=4π/3, зелёный=5π/3.

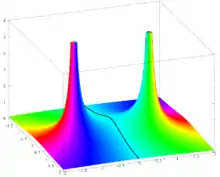
Функция f:R→R, определяемая уравнением

${\displaystyle f(x)={\frac {1}{1+x^{2}}}}$

является вещественной аналитической, то есть, в данной области определяется её рядом Тейлора. Один из рисунков, приведённых выше, показывает, что некоторые очень просто задаваемые функции не могут быть выражены с помощью приближения Тейлора в окрестности центра приближения, если эта окрестность слишком велика. Это свойство легко понять в рамках комплексного анализа. Более конкретно, функция f расширяется до мероморфной функции

${\displaystyle f:\mathbb {C} \cup \{\infty \}\to \mathbb {C} \cup \{\infty \};\quad f(z)={\frac {1}{1+z^{2}}}}$

на компактифицированной комплексной плоскости. Она имеет простые оси в точках z=i и z=−i, и она всюду аналитическая. Её ряд Тейлора, имеющий центром z₀, сходится на любом круге B(z₀,r) с r<|z-z₀|, где тот же ряд Тейлора сходится при z∈C. Вследствие этого ряд Тейлора функции f, имеющий центром точку 0, сходится на B(0,1) и он не сходится для любого z∈C с |z|>1 вследствие имеющихся осей в точках i и −i. По тем же причинам ряд Тейлора функции f, имеющий центром точку 1, сходится на B(1,√2) и не сходится для любого z∈C с |z-1|>√2.

Функция f:Rⁿ → R является дифференцируемой в точке a ∈ Rⁿ тогда и только тогда, когда существует линейная форма L : Rⁿ → R и функция h : Rⁿ → R такая, что

${\displaystyle f({\boldsymbol {x}})=f({\boldsymbol {a}})+L({\boldsymbol {x}}-{\boldsymbol {a}})+h({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}}),\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h({\boldsymbol {x}})=0.}$

Если этот случай имеет место, то L = df(a) является дифференциалом функции f в точке a. Кроме того, когда частные производные функции f существуют в точке a, то дифференциал f в точке a даётся формулой

${\displaystyle df({\boldsymbol {a}})({\boldsymbol {v}})={\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}})v_{1}+\cdots +{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})v_{n}.}$

Вводя мультииндекс, запишем

${\displaystyle |\alpha |=\alpha _{1}+\cdots +\alpha _{n},\quad \alpha$ !=\alpha _{1}!\cdots \alpha _{n}!,\quad {\boldsymbol {x}}^{\alpha }=x_{1}^{\alpha _{1}}\cdots x_{n}^{\alpha _{n}}}

для α ∈ Nⁿ и x ∈ Rⁿ. Если все частные производные k-го порядка функции f : Rⁿ → R являются непрерывными в a ∈ Rⁿ, то, по теореме Клеро, можно изменить порядок смешанных производных в точке a, тогда запись

${\displaystyle D^{\alpha }f={\frac {\partial ^{|\alpha |}f}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{n}^{\alpha _{n}}}},\qquad |\alpha |\leq k}$

для частных производных высших порядков является правомерной в этой ситуации. То же самое является верным, если все частные производные (k − 1)-го порядка функции f существуют в некоторой окрестности точки a и являются дифференцируемыми в точке a. Тогда можно сказать, что функция f является k раз дифференцируемой в точке a .

Теорема Тейлора для функций многих переменных. Пусть f : Rⁿ → R является k раз дифференцируемой функцией в точке a∈Rⁿ. Тогда существует h_α : Rⁿ→R такая, что

${\displaystyle f({\boldsymbol {x}})=\sum _{|\alpha |=0}^{k}{\frac {D^{\alpha }f({\boldsymbol {a}})}{\alpha$ !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\alpha |=k}h_{\alpha }({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha },\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h_{\alpha }({\boldsymbol {x}})=0.}

Если функция f : Rⁿ → R является k+1 раз непрерывно дифференцируемой в замкнутом шаре B, то можно получить точную формулу для остатка разложения Тейлора до частных производных (k+1)-го порядка от f в этой окрестности. А именно

${\displaystyle f({\boldsymbol {x}})=\sum _{|\alpha |=0}^{k}{\frac {D^{\alpha }f({\boldsymbol {a}})}{\alpha$ !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\beta |=k+1}R_{\beta }({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\beta },\qquad R_{\beta }({\boldsymbol {x}})={\frac {|\beta |}{\beta !}}\int _{0}^{1}(1-t)^{|\beta |-1}D^{\beta }f{\big (}{\boldsymbol {a}}+t({\boldsymbol {x}}-{\boldsymbol {a}}){\big )}\,dt.}

В этом случае, вследствие непрерывности частных производных (k+1)-го порядка на компактном множестве B, непосредственно получаем

${\displaystyle {\big |}R_{\beta }({\boldsymbol {x}})|\leq {\frac {|\beta |}{\beta$ !}}\max _{|\alpha |=|\beta |}\max _{{\boldsymbol {y}}\in B}|D^{\alpha }f({\boldsymbol {y}})|,\qquad {\boldsymbol {x}}\in B.}

Пусть[7]

${\displaystyle h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(x-a)^{k}}}&x\not =a\\0&x=a\end{cases}}}$

где, как указано в формулировке теоремы Тейлора,

${\displaystyle P(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.}$

Достаточно показать, что

${\displaystyle \lim _{x\to a}h_{k}(x)=0.}$

Доказательство основано на повторяющемся применении правила Лопиталя. Заметим, что каждое j = 0,1,…,k−1, ${\displaystyle f^{(j)}(a)=P^{(j)}(a)}$. Отсюда каждая следующая производная числителя функции ${\displaystyle h_{k}(x)}$ стремится к нулю в точке ${\displaystyle x=a}$, и то же самое справедливо для знаменателя. Тогда

${\displaystyle {\begin{aligned}\lim _{x\to a}{\frac {f(x)-P(x)}{(x-a)^{k}}}&=\lim _{x\to a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(x-a)^{k}}}=\cdots =\lim _{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))}{{\frac {d^{k-1}}{dx^{k-1}}}(x-a)^{k}}}\\&={\frac {1}{k!}}\lim _{x\to a}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{x-a}}\\&={\frac {1}{k!}}(f^{(k)}(a)-P^{(k)}(a))=0\end{aligned}}}$

где переход от предпоследнего выражения к последнему следует из определения производной в точке x = a.