Тангенциальное ускорение
Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости, в отличие от нормальной компоненты, характеризующей изменение направления скорости.
Определяется как производная модуля скорости по времени, умноженная на единичный вектор вдоль скорости. Обозначается символом, выбранным для ускорения, с добавлением индекса тангенциальной компоненты: или , , . Измеряется в м/с2 (в системе СИ).
Величина равна проекции полного ускорения на касательную в данной точке кривой, что соответствует коэффициенту разложения по сопутствующему базису.
Общая формула
Величину тангенциального ускорения как проекцию вектора ускорения на касательную к траектории можно выразить так:
- ,
где — путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.
Если использовать для единичного касательного вектора обозначение , то можно записать тангенциальное ускорение в векторном виде:
- .
Тангенциальное ускорение параллельно вектору скорости при ускоренном движении (положительная производная) и антипараллельно при замедленном (отрицательная производная).
Происхождение формулы
Разложение полного ускорения на тангенциальную и нормальную компоненты осуществляется посредством дифференцирования по времени вектора скорости, представленного в виде через единичный вектор касательной :
- .
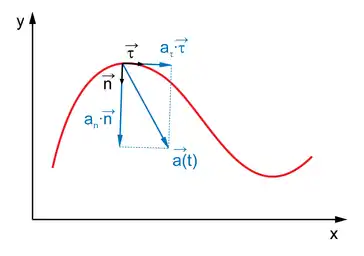
Первое слагаемое — тангенциальное ускорение , а второе — нормальное ускорение ( и — радиус кривизны и единичный вектор нормали к траектории в рассматриваемой точке).
Некоторые примеры
- Пример 1
Скорость камня, сброшенного с высоты с начальной скоростью , направленной горизонтально, до падения на землю будет изменяться как , где — ускорение свободного падения. Модуль скорости составит , а значит, тангенциальное ускорение по величине равняется . В начальный момент оно равно нулю, а при больших стремится к . Можно записать тангенциальное ускорение и как вектор:
- .
В этих выражениях , — единичные векторы в декартовых координатах.
- Пример 2
Пусть радиус-вектор тела зависит от времени по закону .
В таком случае скорость тела найдётся как . Соответственно, её модуль равен и является постоянной величиной. В результате получается, что тангенциальное ускорение — ноль:
- .
Рассмотренная зависимость описывает равномерное движение по окружности радиусом .
Равнопеременность
Движение тела с постоянным по величине тангенциальным ускорением называется равнопеременным. Слова «равнопеременное» (const) и «равноускоренное» (const) не синонимичны. Взаимозаменяемыми данные термины становятся только применительно к прямолинейному движению. Тем не менее возможны определённые аналогии при рассмотрении обоих названных типов движения.