Рывок (кинематика)
Рыво́к — векторная физическая величина, характеризующая темп (скорость) изменения ускорения тела. Является третьей производной по времени от радиус-вектора.
| Рывок | |
|---|---|
| Размерность | LT −3 |
| Единицы измерения | |
| СИ | м/с3 |
| СГС | см/с3 |
| Другие единицы | g/с |
| Примечания | |
| векторная величина | |
Рывок в кинематике
Вектор рывка в любой момент времени находится путём дифференцирования вектора ускорения частицы по времени:
где:
- — ускорение,
- — скорость,
- — радиус-вектор.
Соответственно формулы для движения с постоянным рывком имеют вид:
Формулы можно обобщать и далее на более высокие производные радиус-вектора, вводя в разложение координаты в степенной ряд всё новые и новые члены. По традиции или просто для удобства из-за частого использования первые 3 коэффициента в разложении имеют собственные названия: скорость, ускорение и рывок соответственно.
Единицы измерения рывка
Электродинамика
Сила, действующая на ускоренно движущийся заряд (радиационное трение, или реакция излучения), пропорциональна третьей производной координаты (т. e. первой производной ускорения) по времени.
(в системе СИ).
Применение
Транспорт
Понятие рывка применяется при перевозке пассажиров, а также хрупких и ценных грузов.
Пассажир приспосабливается к ускорению, напрягая мышцы и подбирая позу. При изменении ускорения поза, естественно, тоже меняется. Пассажиру нужно дать время, чтобы отреагировать и сменить её — иначе стоячий пассажир потеряет равновесие, а сидячий — ударится. Типичный пример — момент полной остановки вагона метро после процесса торможения: стоячие пассажиры, наклонившиеся вперёд в процессе торможения, не успевают приспособиться к новому ускорению, возникающему в момент остановки, и наклоняются назад.
Аналогично, груз, к которому приложено ускорение, деформируется. Частое и быстрое изменение ускорения означает частую и быструю деформацию, что может привести к разрушению хрупкого груза. Частично рывок можно уменьшить, использовав амортизирующую упаковку.
Для многих приборов и устройств в технических условиях нормируется предельное значение рывка.
Производные большего порядка в транспорте применяются редко. Известный случай, когда радиус-вектор исследовался до четвёртой производной — вывод на орбиту телескопа Хаббла[1].
В теоретической механике
Применяется в интегрировании по Верле для быстрого численного решения дифференциальных уравнений движения материальных точек.
В статье И. И. Смульского и Я. И. Смульского «Астероид Апофис: эволюция орбиты и возможное использование» используются производные до шестого порядка и ряд Маклорена в программе расчёта.
В работе финского математика К. Зундмана, посвящённой решению «задачи трёх тел», используются высшие производные и ряды.
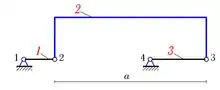
Понятие рывка находит применение и в задаче о вычислении угловых скоростей и угловых ускорений звеньев шарнирного четырёхзвенника — в ситуации, когда все шарниры лежат на одной прямой[2].
Металлорежущие станки
В металлорежущих станках с электронным управлением изменение ускорения также важно — быстрые деформации инструмента, случающиеся при высоком рывке, преждевременно выводят инструмент из строя.
Примечания
- Упоминание о телескопе Хаббла (недоступная ссылка). Дата обращения: 21 февраля 2014. Архивировано 30 ноября 2016 года.
- Кирсанов М. Н. Решения задач по теоретической механике. — М.: ИНФРА-М, 2015. — 216 с. — ISBN 978-5-16-010558-1. — С. 118—119.
Литература
- Кинематика механизмов — статья из Большой советской энциклопедии. Артоболевский И. И., Левитский Н. И.
- Капунцов Ю. Д. Электрооборудование и электропривод промышленных установок. Учебник для вузов. — М.: Высшая школа, 1979. — 360 с. Архивная копия от 8 марта 2008 на Wayback Machine
- Хитрик В. Э. Методы динамической оптимизации механизмов машин-автоматов. — М.: Изд-во Ленингр. ун-та, 1974. — 116 с. Архивная копия от 14 октября 2008 на Wayback Machine
