Расщепляемый граф

В теории графов расщепляемым графом называется граф, в котором вершины можно разделить на клику и независимое множество. Расщепляемые графы впервые изучали Фёлдес и Хаммер[1][2], и независимо ввели Тышкевич и Черняк[3][4].

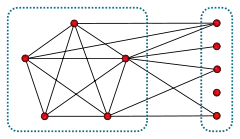
Расщепляемый граф, разделённый на клику и независимое множество.

Расщепляемый граф может иметь несколько разложений на клику и независимое множество. Так, путь a-b-c является расщепляемым и может быть разбит тремя разными способами:

  1. клика {a,b} и независимое множество {c}
  2. клика {b,c} и независимое множество {a}
  3. клика {b} и независимое множество {a,c}

Расщепляемые графы можно охарактеризовать в терминах их запрещённых подграфов — граф расщепляем в том и только в том случае, когда никакой порождённый подграф не является циклом с четырьмя или пятью вершинами, а также нет пары несвязных вершин (то есть дополнения цикла из 4 вершин)[5][6].

Связь с другими семействами графов

По определению, класс расщепляемых графов замкнут по отношению к операции дополнения[7]. Ещё одна характеристика расщепляемых графов, вовлекающая дополнение — это хордальные графы, дополнения которых также хордальны[8]. Поскольку хордальные графы являются графами пересечений поддеревьев деревьев, расщепляемые графы являются графами пересечений различных подзвёзд звёзд[9]. Почти все хордальные графы являются расщепляемыми графами. То есть, при стремлении n к бесконечности, частное от числа хордальных графов с n вершинами к числу разделяемых графов стремится к единице[10].

Поскольку хордальные графы являются совершенными, то расщепляемые графы тоже совершенны. Двойные расщепляемые графы, семейство графов, полученных из расщепляемых графов удвоением числа вершин (так что клика даёт антисочетание — множество рёбер, находящихся на расстоянии не более 2 друг от друга, а независимое множество превращается в паросочетание), появляется как один из пяти основных классов совершенных графов, из которых можно построить все остальные в доказательство строгой теоремы о совершенных графах[11].

Если граф и расщепляемый и интервальный, то его дополнение является и расщепляемым, и графом сравнимости, и наоборот. Расщепляемые графы сравнимости, а следовательно и расщепляемые интервальные графы, можно описать в терминах трёх запрещённых подграфов[12]. Расщепляемые кографы — это в точности пороговые графы, а расщепляемые графы перестановки — это в точности интервальные графы, дополнения которых тоже являются интервальными[13]. Кохроматическое число расщепляемых графов равно 2.

Максимальная клика и максимальное независимое множество

Пусть G — расщепляемый граф, разложенный на клику C и независимое множество I. Тогда любая максимальная клика в расщеплённом графе либо совпадает с C, либо является окрестностью вершины из I. Таким образом, в расщепляемом графе легко найти максимальную клику и, кроме того, максимальное независимое множество . В любом расщепляемом графе должно выполняться одно из следующих утверждений[14]:

  1. Существует вершина x в I, такая что C ∪ {x} является полным. В этом случае, C ∪ {x} — максимальная клика и I — максимальное независимое множество.
  2. Существует вершина x в C, такая что I ∪ {x} — независимое множество. В этом случае I ∪ {x} — максимальное независимое множество и C — максимальная клика.
  3. C является наибольшей кликой и I наибольшим независимым множеством. В этом случае G имеет единственное разложение (C, I) на клику и независимое множество, C является максимальной кликой, и I является максимальным независимым множеством.

Некоторые другие оптимизационные задачи, NP-полные на более общих семействах графов, включая раскраску, решаются просто на расщепляемых графах.

Последовательности степеней

Одно из замечательных свойств расщепляемых графов — это то, что они могут быть распознаны чисто по их последовательностям степеней вершин. Пусть d1 ≥ d2 ≥ … ≥ dn — последовательность степеней вершин графа G и m — наибольшее значение i, для которого di ≥ i — 1. Тогда G является расщепляемым графом в том и только в том случае, когда

Если это выполняется, то m вершин с наибольшими степенями образуют максимальную клику G, а оставшиеся вершины дадут независимое множество[15].

Подсчёт расщепляемых графов

Ройл[16] показал, что расщепляемые графы с n вершинами один к одному соответствуют некоторым семействам Спернера. Используя этот факт он нашёл формулу числа (неизоморфных) расщепляемых графов с n вершинами. Для малых значений n, начиная с n = 1, эти числа равны

1, 2, 4, 9, 21, 56, 164, 557, 2223, 10766, 64956, 501696, … последовательность A048194 в OEIS.

Это перечисление ранее доказали Тышкевич и Черняк[17].

Примечания
  1. Földes, Hammer, 1977a.
  2. Földes, Hammer, 1977b.
  3. Тышкевич, Черняк, 1979.
  4. Фёлдес и ХаммерFöldes, Hammer, 1977a дали более общее определение, в котором графы, которые они называют расщепляемыми, включают также двудольные графы (то есть, графы, разбитые на два независимых множества) и дополнения двудольных графов (то есть, графы, которые можно разложить на две клики). Фёлдер и Хаммер Földes, Hammer, 1977b дают определение, приведённое здесь и которое используются в последующей литературе, например у Брандштэдта, Ли и СпинрадаBrandstädt, Le, Spinrad, 1999, Определение 3.2.3, с. 41
  5. Földes, Hammer, 1977a; Golumbic, 1980, теорема 6.3, стр. 151.
  6. Pinar Heggernes, Dieter Kratsch. Linear-time certifying recognition algorithms and forbidden induced subgraphs // Nordic Journal of Computing. — 2007. — Т. 14.
  7. Golumbic, 1980, теорема 6.1, стр. 150.
  8. Földes, Hammer, 1977a; Golumbic, 1980, теорема 6.3, стр. 151; Brandstädt, Le, Spinrad, 1999, теорема 3.2.3, p. 41.
  9. McMorris, Shier, 1983; Voss, 1985; Brandstädt, Le, Spinrad, 1999, теорема 4.4.2, стр. 52.
  10. Bender, Richmond, Wormald, 1985.
  11. Chudnovsky, Robertson, Seymour, Thomas, 2006.
  12. Földes, Hammer, 1977b; Golumbic, 1980, теорема 9.7, стр. 212.
  13. Brandstädt, Le, Spinrad, 1999, следствие 7.1.1 стр. 106 и теорема 7.1.2 стр. 107.
  14. Hammer, Simeone, 1981; Golumbic, 1980, теорема 6.2, стр. 150.
  15. Hammer, Simeone, 1981; Тышкевич, 1980; Тышкевич, Мельников, Котов, 1981; Golumbic, 1980, теорема 6.7 и следствие 6.8, стр. 154; Brandstädt, Le, Spinrad, 1999, теорема 13.3.2, стр. 203. Merris, 2003 дальнейшее рассмотрение последовательности степеней расщепляемых графов.
  16. Royle, 2000.
  17. Тышкевич, Черняк, 1990.

Литература
  • E. A. Bender, L. B. Richmond, N. C. Wormald. Almost all chordal graphs split // J. Austral. Math. Soc.. — 1985. — Т. 38, вып. 2. — С. 214—221. — doi:10.1017/S1446788700023077.
  • Andreas Brandstädt, Van Bang Le, Jeremy Spinrad. Graph Classes: A Survey. — SIAM Monographs on Discrete Mathematics and Applications, 1999. — ISBN 0-89871-432-X.
  • Maria Chudnovsky, Neil Robertson, Paul Seymour, Robin Thomas. The strong perfect graph theorem // Annals of Mathematics. — 2006. — Т. 164, вып. 1. — С. 51—229. — doi:10.4007/annals.2006.164.51.
  • Stéphane Földes, Peter L. Hammer. Congressus Numerantium. — Winnipeg: Utilitas Math., 1977a. — Т. XIX. — С. 311—315.
  • Stéphane Földes, Peter L. Hammer. Split graphs having Dilworth number two // Canadian Journal of Mathematics. — 1977b. — Vol. 29. — Вып. 3. — С. 666—672. — doi:10.4153/CJM-1977-069-1.
  • Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs. — Academic Press, 1980. — ISBN 0-12-289260-7.
  • Peter L. Hammer, Bruno Simeone. The splittance of a graph // Combinatorica. — 1981. — Т. 1, вып. 3. — С. 275—284. — doi:10.1007/BF02579333.
  • F. R. McMorris, D. R. Shier. Representing chordal graphs on K1,n // Commentationes Mathematicae Universitatis Carolinae. — 1983. — Т. 24. — С. 489—494.
  • Russell Merris. Split graphs // European Journal of Combinatorics. — 2003. — Т. 24, вып. 4. — С. 413—430. — doi:10.1016/S0195-6698(03)00030-1.
  • Gordon F. Royle. Counting set covers and split graphs // Journal of Integer Sequences. — 2000. — Т. 3, вып. 2. — С. 00.2.6.
  • Регина И. Тышкевич. Каноническое разложение графа // Доклады Академии Наук БССР. — 1980. — Т. 24, вып. 8. — С. 677—679.
  • Р. И. Тышкевич, А. А. Черняк. Каноническое разложение графа, определяемого степенями его вершин // Известия АН БССР, сер. физ.-мат. наук. — 1979. — Т. 5. — С. 14—26.
  • Р. И. Тышкевич, А. А. Черняк. Еще один метод перечисления непомеченных комбинаторных объектов // Matem. Zametki. — 1990. — Т. 48, вып. 6. — С. 98—105.
  • Р. И. Тышкевич, О. И. Мельников, В. М. Котов. О графах и степенных последовательностях: каноническое разложение // Кибернетика. — 1981. — Т. 6. — С. 5—8.
  • H.-J. Voss. Note on a paper of McMorris and Shier // Commentationes Mathematicae Universitatis Carolinae. — 1985. — Т. 26. — С. 319—322.

Дальнейшее чтение
  • Главу о расщепляемых графах можно прочесть в книге Мартина Чарльза Голумбика (Martin Charles Golumbic) «Algorithmic Graph Theory and Perfect Graphs».
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.