Пороговый граф
В теории графов пороговый граф — это граф, который может быть построен из одновершинного графа последовательным выполнением следующих двух операций:
- Добавление в граф одной изолированной вершины
- Добавление одной доминирующей вершины в граф, т.е. отдельной вершины, связанной со всеми остальными вершинами.
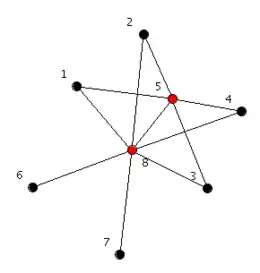
Например, граф на рисунке является пороговым графом. Он может быть построен с одной вершины (вершина 1), и добавления чёрных вершин как изолированных вершин и красных вершин как доминирующих вершин в порядке нумерации.
Пороговые графы были введены Хваталом и Хаммером[1]. Глава, посвящённая графам, появилась в книге Голумбика[2], а книга Махадева и Пеледа[3] полностью посвящена пороговым графам.
Альтернативные определения
Эквивалентное определение следующее: граф является пороговым, если существует вещественное число и для каждой вершины задан вес , такой, что для любых двух вершин , является ребром тогда и только тогда, когда .
Другое эквивалентное определение: граф является пороговым, если существует вещественное число и для каждой вершины задан вес , такой, что для любого множества вершин , является независимым тогда и только тогда, когда
Название "пороговый граф" пришёл из определения: S является "порогом" для свойства иметь ребро, или, эквивалентно, T является порогом для множества быть независимым.
Разложение
Из определения, использующего последовательное добавление вершин, можно получить альтернативный путь уникального описания порогового графа в смысле строки символов. всегда служит первым символом строки и представляет первую вершину графа. Каждый последующий символ будет либо , который означает изолированную вершину, либо , который означает добавление доминирующей вершины. Например, строка представляет звезду с тремя листьями, а представляет путь из трёх вершин. Граф на рисунке можно представить строкой
Связные классы графов и распознавание
Пороговые графы являются специальным случаем Кографов, расщепляемых графов и тривиально совершенных графов[4]. Любой граф, являющийся одновременно кографом и расщепляемым графом, является пороговым. Любой граф, являющийся одновременно тривиально совершенным графом и дополнением тривиально совершенного графа, является пороговым графом. Пороговые графы являются также специальным случаем интервальных графов. Все эти связи могут быть объяснены в терминах их характеризации запрещёнными порождёнными подграфами. Кограф — это граф с отсутствием порождённых путей с четырьмя вершинами, P4, а пороговые графы — это графы баз порождённых подграфов P4, C4 или 2K2 [5]. C4 — это цикл из четырёх вершин , а 2K2 — его дополнение, то есть два раздельных ребра. Это также объясняет, почему пороговые графы замкнуты по взятию дополнения. P4 является самодополнительным, а потому, если граф не содержит порождённые подграфы P4, C4 и 2K2, его дополнение тоже не будет их иметь [6].
Хеггернес и др. показали, что пороговые графы могут быть распознаны за линейное время. Если граф не является пороговым, препятствие в виде P4, C4 или 2K2 будет указано.
Примечания
- Chvátal, Hammer, 1977.
- Golumbic, 1980.
- Mahadev, Peled, 1995.
- Емеличев, Мельников, Сарванов, Тышкевич, 1990, с. 227, Следствие 50.11.
- Емеличев, Мельников, Сарванов, Тышкевич, 1990, с. 224, Следствие 50.3.
- Емеличев, Мельников, Сарванов, Тышкевич, 1990, с. 227, Следствие 50.12.
Литература
- В.А.Емеличев, О.И. Мельников, В.И. Сарванов, Р.И. Тышкевич. Лекции по теории графов. — Москва: «Наука», 1990. — ISBN 5-02-013992-0. §50. Пороговые графы
- Václav Chvátal, Peter Ladislaw Hammer. Studies in Integer Programming (Proc. Worksh. Bonn 1975) / P. L. Hammer, E. L. Johnson, B. H. Korte, G. L. Nemhauser. — Amsterdam: North-Holland, 1977. — Т. 1. — С. 145–162. — (Annals of Discrete Mathematics)..
- Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs. — New York: Academic Press, 1980.. 2nd edition, Annals of Discrete Mathematics, 57, Elsevier, 2004.
- N. V. R. Mahadev, Uri N. Peled. Threshold Graphs and Related Topics. — Elsevier, 1995..
Ссылки
- Threshold graphs, Information System on Graph Classes and their Inclusions.