Граф-звезда

Граф-звезда — связный граф в котором всё рёбра исходят из одной вершины. Звезда с вершиной обычно обозначается , при этом называют порядком звезды.

Граф-звезда S7

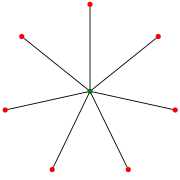
Другие определения
  • дерево с одним внутренним узлом и k листьями. Кроме того, некоторые авторы определяют Sk как дерево порядка k с максимальным диаметром 2; тогда граф-звезда k > 2 имеет k — 1 листьев.

Граф-звезда с тремя ребрами называется лапа или клешня[2] (англ. claw).

Граф-звезда Sk обладает изяществом вершин, когда k чётно, и не обладает, если к нечётно.

Граф-звезда также может быть описан как связный граф, в котором не более одной вершины имеет степень больше единицы.

Отношение к другим видам графов

Графы-клешни важны в определении графов без клешней, графов, которые не имеют подграфов, являющихся клешнями[3][4].

Граф-звезда является особым видом дерева. Как и любое дерево, граф-звезда может быть закодирован при помощи последовательности Прюфера (англ. Prüfer sequence); последовательность Прюфера для графа-звезды K1,k состоит из k − 1 копии центральной вершины[5].

Графы S3, S4, S5 и S6.

Другие применения

Множество расстояний между вершинами графа-клешни представляет собой пример метрического пространства, которое не может быть встроено изометрически в евклидово пространство любой размерности[6].

Топология компьютерной сети «Звезда», построенная в виде графа-звезды, играет важную роль в распределённых вычислениях.

Примечания
  1. Публичные учебные материалы ВГУЭС
  2. В.А. Евстигнеев, В.Н. Касьянов. Словарь по графам в информатике. — Новосибирск. — (Конструирование и оптимизация программ). — ISBN 978-591124-036-3.
  3. Faudree, Ralph; Flandrin, Evelyne & Ryjáček, Zdeněk (1997), Claw-free graphs — A survey, Discrete Mathematics Т. 164 (1–3): 87–147, DOI 10.1016/S0012-365X(96)00045-3.
  4. Chudnovsky, Maria & Seymour, Paul (2005), The structure of claw-free graphs, Surveys in combinatorics 2005, vol. 327, London Math. Soc. Lecture Note Ser., Cambridge: Cambridge Univ. Press, с. 153–171, <http://www.columbia.edu/~mc2775/claws_survey.pdf> Архивная копия от 23 октября 2012 на Wayback Machine.
  5. Gottlieb, J.; Julstrom, B. A.; Rothlauf, F. & Raidl, G. R. (2001), Prüfer numbers: A poor representation of spanning trees for evolutionary search, Proc. Genetic and Evolutionary Computation Conference, Morgan Kaufmann, с. 343–350, <http://www.ads.tuwien.ac.at/publications/bib/pdf/gottlieb-01.pdf>. Проверено 4 января 2013. Архивная копия от 26 сентября 2006 на Wayback Machine.
  6. Linial, Nathan (2002), Finite metric spaces–combinatorics, geometry and algorithms, Proc. International Congress of Mathematicians, Beijing, vol. 3, с. 573–586
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.