Параллель
Паралле́ль — линия сечения поверхности планеты плоскостью, параллельной плоскости экватора.
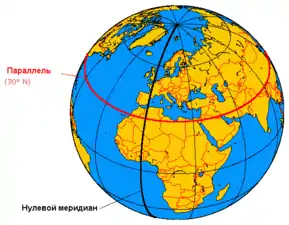
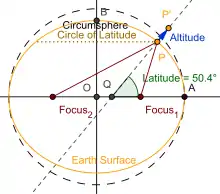
На глобусе
На глобусе параллель рисуется в виде окружности, все точки которой равноудалены от экватора. Все точки одной параллели имеют одинаковую широту, но различную долготу. Длины параллелей различны: они увеличиваются при приближении к экватору и уменьшаются — к полюсам. Экватор — самая длинная параллель.
На Земле
Длина дуги параллели в 1° по долготе
Чтобы найти для любой параллели длину дуги в 1°, нужно умножить 111,3 км (длину дуги экватора в 1°) на косинус угла, соответствующего географической широте искомой параллели. Например, на широтах с шагом 15° получаем:
15° — 108 км
30° — 96 км
45° — 79 км
60° — 56 км
75° — 29 км
90° — 0 км
Принято определение экватора как нулевой параллели. Северный полюс имеет широту +90 градусов, Южный полюс — −90°. Расстояние между двумя параллелями (фактически — дуга меридиана), которые отличаются на 1° по широте, — примерно 111 км.
Параллели (кроме экватора) не являются ортодромиями, то есть кратчайшими линиями на поверхности между любыми их двумя точками.
Основные широты
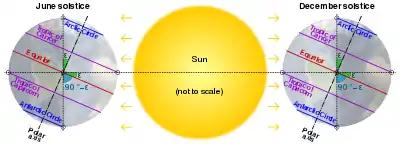
Существует пять основных широт, перечисленных ниже с севера на юг. Положение экватора является фиксированным (90 градусов от оси вращения Земли), но показатели других широт зависят от наклона оси относительно плоскости орбиты Земли, и поэтому не являются идеально фиксированными. Приведённые ниже значения даны на 20 сентября 2020[1]:
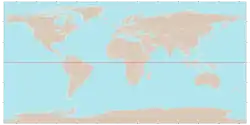
- Северный полярный круг — 66°33′48,0″ с. ш.
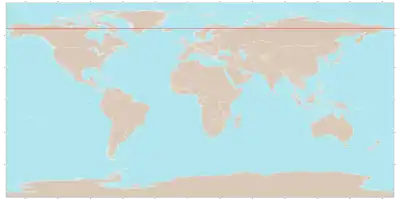
- Северный тропик (Тропик Рака) — 23°26′12,0″ с. ш.
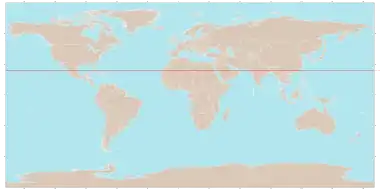
- Экватор — 0° широты
- Южный тропик (Тропик Козерога) — 23°26′12,0″ ю. ш.
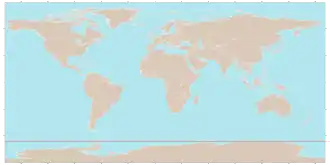
- Южный полярный круг — 66°33′48,0″ ю. ш.
Эти широты, за исключением экватора, отмечают различия между пятью основными географическими зонами.
Параллели как государственные и административные границы
Параллели могут использоваться для обозначения границ между регионами или странами.
- 70° с. ш.: часть границы между канадскими территориями Нунавут (Ю) и Северо-Западные территории (С) на о. Виктория.
- 67° с. ш.: Россия, часть границы Ненецкого автономного округа (С) и Республики Коми (Ю).
- 60° с. ш.: в Канаде, граница Юкона (С) и Британской Колумбии (Ю), а также Северо-Западных территорий (C) с Британской Колумбией, Альбертой и Саскачеваном (Ю), а также материковой части Нунавута (С) с Манитобой (Ю).
- 54°40' с. ш.: южная граница Русской Америки с 1825 г.
- 52° с. ш.: часть границы между канадскими провинциями Ньюфаундленд и Лабрадор (С) и Квебек (Ю).
- 51° с. ш.: южная граница Русской Америки с 1799 по 1821 гг.
- 49° с. ш.: бо́льшая часть протяжённости границы между Канадой (С) и США (Ю).
- 48° с. ш.: часть границы между канадскими провинциями Квебек (С) и Нью-Брансуик (Ю).
- 46° с. ш.: часть границы между американскими штатами Вашингтон (С) и Орегон (Ю),
- 46° с. ш.: Казахстан, граница Карагандинской (С) области с Туркестанской (Ю) и Жамбылской (Ю) областями.
- 45° с. ш.: часть границы между Канадой (С) и США (Ю); почти вся граница между американскими штатами Вайоминг (С) и Монтана (Ю).
- 43°30' с. ш.: США, граница между штатами Миннесота (С) и Айова (Ю).
- 43° с. ш.: США, бо́льшая часть протяжённости границы между штатами Южная Дакота (С) и Небраска (Ю).
- 42°30' с. ш.: США, граница между штатами Висконсин (С) и Иллинойс (Ю).
- 42° с. ш.: США, граница между штатами Орегон (С) и Калифорния (Ю); Орегон (С) и Невада (Ю); Айдахо (С) и Невада (Ю); Айдахо (С) и Юта (Ю); была установлена по северной границе Новой Испании, существовавшей в начале 19 века. Кроме того, по этой параллели проведена бо́льшая часть протяжённости границы между американскими штатами Пенсильвания (С) и Нью-Йорк (Ю).
- 41° с. ш.: США, граница между штатами Вайоминг (С) и Колорадо (Ю); часть границы между штатами Вайоминг (С) и Юта (Ю), Вайоминг (С) и Колорадо (Ю).
- 40° с. ш.: США, граница между штатами Небраска (С) и Канзас (Ю).
- 38° с. ш.: граница между зонами советской (С) и американской (Ю) оккупации Кореи с 1945 г. до начала Корейской войны (1950—1953).
- 37° с. ш.: США, граница между штатами Юта, Колорадо и Канзас (С) и Аризона, Нью-Мексико и Оклахома (Ю)
- 36° с. ш.: США, небольшая часть границы между штатами Миссури (С) и Арканзас (Ю)
- 35° с. ш.: США, граница между штатами Теннесси и Северная Каролина (С) и Миссисипи, Алабама и Джорджия (Ю).
- 33° с. ш.: США, часть границы между штатами Арканзас (С) и Луизиана (Ю).
- 32° с. ш.: США, часть границы между штатами Нью-Мексико (С) и Техас (Ю).
- 31°20' с. ш.: часть границы между США (С) и Мексикой (Ю).
- 31° с. ш.: часть границы между Ираном (С) и Ираком (Ю).
- 31° с. ш.: США, часть границы между штатами Миссисипи (С) и Луизиана (Ю), а также между штатами Алабама (С) и Флорида (Ю).
- 28° с. ш.: Мексика, граница между штатами Нижняя Калифорния (С) и Южная Нижняя Калифорния (Ю).
- 27° с. ш.: Ливия, граница между муниципалитетами Эль-Вахат (С) и Эль-Куфра (Ю).
- 26° с. ш.: часть границы между Западной Сахарой (С) и Мавританией (Ю).
- 25° с. ш.: часть границы между Мавританией (С) и Мали (Ю).
- 22° с. ш.: бо́льшая часть границы между Египтом (С) и Суданом (Ю).
- 20° с. ш.: небольшая часть границы между Ливией (С) и Суданом (Ю).
- 20° с. ш.: Судан, граница между штатами Северный (С) и Северный Дарфур (Ю).
- 19° с. ш.: Мавритания, граница между областями Иншири и Адрар (С) и Трарза (Ю).
- 17° с. ш.: граница с демилитаризованной зоной между бывшими Демократической Республикой Вьетнам и Южным Вьетнамом до начала Вьетнамской войны.
- 15°30' с. ш.: часть границы между Мавританией (С) и Мали (Ю).
- 1° ю. ш.: часть границы между Угандой (С) и Танзанией (Ю).
- 5° ю. ш.: Демократическая Республика Конго: часть границ между провинциями Маниема и Южное Киву (С) и Ломами и Танганьика (Ю)
- 8° ю. ш.: Папуа — Новая Гвинея, граница между регионами Момасе (С) и Папуа (Ю).
- 13° ю. ш.: часть границы между Анголой и Замбией
- 21° ю. ш.: Ботсвана, граница между округами Северо-Западный (С) и Ганзи (Ю).
- 21° ю. ш.: Боливия, часть границы между департаментами Чукисака (С) и Тариха (Ю).
- 22° ю. ш.: часть границы между Намибией (С) и Ботсваной (Ю).
- 26° ю. ш.: Австралия, часть границы между Северной территорией и штатом Квинсленд (С) и штатом Южная Австралия (Ю).
- 28° ю. ш.: Аргентина, граница между провинциями Чако (С) и Санта-Фе (Ю).
- 29° ю. ш.: Австралия, часть границы между штатами Квинсленд (С) и Новый Южный Уэльс (Ю).
- 35° ю. ш.: Аргентина, граница между провинциями Кордова (С) и Ла-Пампа (Ю).
- 36° ю. ш.: Аргентина, граница между провинциями Мендоса (частично) и Сан-Луис (С) и Ла-Пампа (Ю).
- 42° ю. ш.: Аргентина, граница между провинциями Рио-Негро (С) и Чубут (Ю).
- 46° ю. ш.: Аргентина, граница между провинциями Чубут (С) и Санта-Крус (Ю).
- 52° ю. ш.: часть границы между Аргентиной (С) и Чили (Ю)
См. также
- Географические координаты
- 45-я Параллель (улица в Ставрополе)
Примечания
- «Trópico en movimiento» (in Spanish). Groups.google.com. Дата обращения: 13 мая 2014.
Ссылки
- U.S. Naval Observatory — mean obliquity of the ecliptic Архивная копия от 12 октября 2007 на Wayback Machine