Теория гомоцентрических сфер

Рис. 1. Движение Солнца в модели двух сфер (T — Земля). Внешняя сфера отвечает за суточное движение Солнца, внутренняя — за годичное

Согласно Симпликию, Платон поставил перед своими учениками задачу представить движение планет в виде комбинации равномерных круговых движений, и первым, кто её решил, был Евдокс Книдский, создавший первую теорию гомоцентрических (или концентрических) сфер.

Эта теория была изложена в книге О скоростях, которая до нас не дошла, но основные идеи Евдокса привели Аристотель и (чуть более подробно) Симпликий. Реконструкцию этой теории впервые предложил в 1877 году итальянский астроном Джиованни Скиапарелли.

Солнце

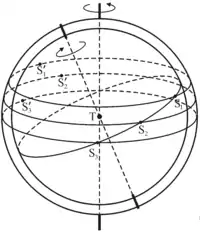
В модели Евдокса видимое движение Солнца является результатом сложения трёх равномерных круговых движений. Двумя из них являются вращение вместе с небесной сферой (с периодом в одни сутки, с востока на запад) и вдоль эклиптики (с периодом в один год, с запада на восток). Такой характер движения представляется с помощью следующей промежуточной модели: внутри сферы, вращающейся вокруг закреплённой оси с периодом в одни сутки, закреплена ось, вокруг которой (в противоположном направлении) с периодом в один год вращается ещё одна сфера (рис. 1). Центры сфер совпадают, Земля расположена в центре, Солнце находится на экваторе внутренней сферы (эклиптике). Во времена Евдокса ошибочно считалось, что Солнце движется не точно по эклиптике, а отклоняется от неё в направлении север-юг, поэтому Евдокс Книдский добавил ещё одну сферу с очень большим периодом обращения (неизвестно, каким именно). Порядок сфер должен был быть таким: снаружи находилась сфера, отвечавшая за суточное вращение, к ней внутри была прикреплена сфера, отвечавшая за отклонение Солнца от эклиптики, и уже к ней внутри была прикреплена сфера, отвечавшая за годичное движение Солнца по эклиптике. Неравномерность движения Солнца по эклиптике, которая уже была известна во времена Евдокса, в этой модели не учитывалась.

Рис. 2. Система из четырёх концентрических сфер, использовавшаяся для моделирования движения планет в теории Евдокса. Цифрами обозначены сферы, отвечавшие за суточное вращение небосвода (1), за движение вдоль эклиптики (2), за попятные движения планеты (3 и 4). T — Земля, пунктирная линия изображает эклиптику (экватор второй сферы)

Планеты

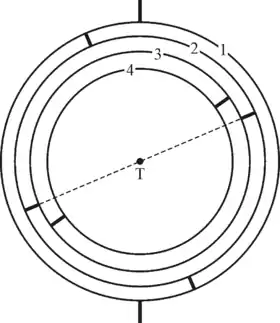
Движение пяти известных в древности планет Евдокс описал с помощью четырёх сфер: внешняя (период обращения одни сутки) описывает суточное движение планеты, вторая (период обращения равен сидерическому периоду планеты) описывает движение планеты по зодиаку, и в неё были последовательно вложены ещё две сферы, отвечавшие за попятные движения планеты (рис. 2). По Симпликию, третья и четвёртая сферы вращаются навстречу друг другу с одинаковыми периодами, равными синодическому периоду планеты; ось третьей сферы лежит на экваторе второй (то есть на эклиптике); ось четвёртой сферы наклонена по отношению к третьей; сочетание движений по этим сферам приводит к тому, что траектория планеты оказывается похожей на восьмёрку. Эту кривую Евдокс назвал гиппопедой, поскольку по форме она схожа с лошадиными путами. Симпликий приводит также некоторые численные параметры. По этим данным с определённостью восстановить планетную теорию Евдокса невозможно. Описание Аристотеля ещё менее подробно. Выдающейся заслугой Скиапарелли была реконструкция этой теории.

Рис. 3. Третья (наружная) и четвёртая (внутренняя) сферы в планетной теории Евдокса согласно реконструкции Скиапарелли (а) и Веселовского-Яветца (б). Угловые скорости приведены относительно второй сферы (для третьей сферы) и относительно третьей сферы (для четвёртой сферы). T — Земля

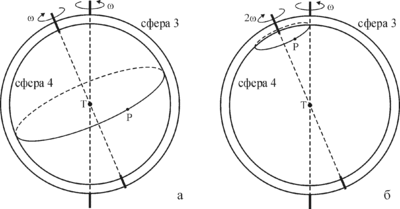
В реконструкции Скиапарелли предполагается, что планета находится на экваторе четвёртой сферы (о чем не говорится ни у Симпликия, ни у Аристотеля). Кроме того, слова Симпликия о равенстве периодов обращений этих двух сфер интерпретируется таким образом, что равны друг другу период (и, соответственно, угловая скорость) обращения третьей сферы относительно второй и четвёртой относительно третьей (рис. 3,а). Таким образом, если бы оси вращения этих сфер совпадали, то относительно внешнего наблюдателя планета была бы неподвижной. Скиапарелли показал, что сложение равномерных вращений, обладающих такими свойствами, действительно приводит к восьмеркообразной траектории, вид которой совпадает с описанием гиппопеды (рис. 4,а)[1].

Рис. 4. Гиппопеда согласно реконструкции Скиапарелли (а) и Веселовского-Яветца (б). Числа обозначают положение планеты в последовательные моменты времени

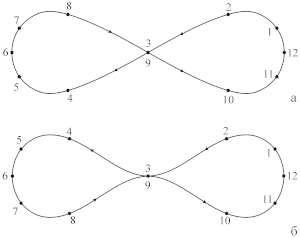
Поскольку ось третьей сферы располагается в плоскости эклиптики (на экваторе второй), то для получения траектории планеты среди звёзд необходимо представить себе, что гиппопеда перемещается вдоль своей длины (влево в горизонтальном направлении на рис. 4,а). При этом между точками 1 и 7 имеет место прямое движение планеты, в районе точки 7 планета поворачивает, совершает попятное движение вплоть до точки 12, затем вновь поворачивает и снова совершает прямое движение. При этом планета пересекает плоскость эклиптики трижды (когда она находится в точках гиппопеды 6, 9 и 12). В этом кроется существенный недостаток теории Евдокса (в реконструкции Скиапарелли), поскольку во время попятного движения планета либо не пересекает эклиптику вовсе (если планета описывает петлю), либо пересекает лишь один раз (если она описывает зигзаг). Но самая большая проблема этой теории — то, что она вообще не может воспроизвести попятные движения некоторых планет, а именно, Марса и Венеры[2].

Альтернативную реконструкцию планетной теории Евдокса предложили советский историк науки Иван Николаевич Веселовский и израильский учёный Идо Яветц[3]. В этой реконструкции предполагается, что угол между планетой и полюсом третьей сферы равен углу между полюсами третьей и четвёртой сфер, то есть планета не находится на экваторе четвёртой сферы, как в модели Скиапарелли (рис. 3,б). Второе отличие от традиционной интерпретации заключается в трактовке свидетельства Симпликия о равенстве периодов обращений сфер: предполагается, что имелись в виду периоды вращения и третьей, и четвёртой сфер относительно второй. Это возможно только в том случае, если угловая скорость вращения третьей сферы относительно четвёртой в два раза превышает угловую скорость четвёртой сферы относительно третьей (то есть при совпадении осей вращения этих сфер планета двигалась бы по кругу). В реконструкции Веселовского—Яветца комбинация движений по третьей и четвёртой сферам приводит к восьмеркообразной траектории, но её ветви не пересекаются в центре, а касаются (рис. 4,б). Существуют некоторые косвенные доводы в пользу версии Скиапарелли[4]. Возможно, только обнаружение новых документов поможет окончательно прояснить этот вопрос.

В любом случае, для моделирования небесных движений Евдоксу в общей сложности понадобилось 27 сфер: одна для неподвижных звёзд, по три для Солнца и Луны, по четыре для пяти планет.

Рис. 5. Кривая, по которой двигались среди звёзд планеты Марс, Венера и Меркурий в результате комбинации движений трёх внутренних сфер согласно теории Каллиппа

Развитием теории концентрических сфер занялся Каллипп из Кизика, живший поколением позже Евдокса и иногда считающийся его учеником. Вероятно, целью Каллиппа было моделирование неравномерности движения Солнца и Луны вдоль эклиптики и объяснение попятных движений Марса и Венеры, отсутствовавших у Евдокса. Каллипп добавил по двум дополнительным сферам для Луны и Солнца и по одной сфере для Марса, Венеры и Меркурия, в то время как модели для Юпитер и Сатурна оставил без изменений. Таким образом, в системе Каллиппа количество сфер возросло до 34.

По предположению Скиапарелли, две дополнительные сферы Солнца и Луны могли создавать маленькие гиппопеды, изменявшие скорость их движения вдоль эклиптики. В случае планет, три внутренних сферы у Каллиппа вместо двух у Евдокса приводили к изменению формы гиппопеды (появляется как бы по бантику на вершинах, рис. 5), что позволяло смоделировать попятные движения Марса и Венеры и уточняло модель Меркурия[5] .

По свидетельству Аристотеля, астрономы более раннего периода полагали планеты движущимися самостоятельно, не будучи прикреплёнными к каким-либо материальным оболочкам[6], так что Евдокс и Каллипп вряд ли считали теорию сфер физической моделью устройства планетной системы (скорее всего, лишь математическим способом вычисления положений планет на небе). «Материализацию» сфер Аристотель считал своим собственным достижением. Теория гомоцентрических сфер полностью соответствовала его философии, где предполагалось, что «надлунный» мир состоит из особого небесного элемента — эфира, свойством которого является неизменность и вечность; отсюда следовало, что небесные тела должны совершать равномерное движение по окружностям, центр которых совпадает с центром мира. Разработку «физического» обоснования теории гомоцентрических сфер Аристотель осуществил в своём трактате Метафизика[7]. В теории Аристотеля сферы механически связаны, причём движение от каждой внешней сферы передаётся внутренним. Отсюда следует, что эти сферы должны были быть твёрдыми; кроме того, поскольку мы видим сквозь них, они должны были быть прозрачными, как хрусталь.

В модель Каллиппа, которая была математической основой его системы, Аристотель добавил дополнительные сферы, единственным назначением которых было компенсировать движение вышележащих сфер. Таким образом, Аристотель был вынужден добавить по четыре сферы Солнцу, Меркурию и Марсу и по три сферы Юпитеру и Сатурну (светила перечислены в порядке удаления от Земли в системе Аристотеля). Итого, в его системе мира движения небесных тел объяснялись посредством 56 сфер.

Древним астрономам было известно, что в некоторых существенных элементах эта теория противоречит наблюдаемым явлениям, причём это противоречие невозможно было преодолеть введением новых сфер. Проблема заключалась в самой сущности теории: каждое из светил движется по сфере, центр которой совпадает с центром Земли, то есть расстояние от светила до Земли должно оставаться неизменным. Но греки уже хорошо знали, что это не так:

1. Некоторые планеты очень сильно меняют свой блеск (например, Марс в середине попятного движения выглядит значительно «больше», чем в другое время);
2. Луна даже при наблюдении невооружённым глазом при одних и тех же условиях не всегда имеет один и тот же угловой размер;
3. Наблюдения Луны с угломерными инструментами показывают, что её видимый размер меняется в отношении 11 к 12;
4. Солнечные затмения, бывают полными (когда диск Солнца полностью закрыт Луной) или кольцеобразными (когда диск Луны немного меньше диска Солнца).

Все эти факты несовместимы с предположением о неизменности расстояний небесных тел от Земли.

Согласно Симпликию, обо всех этих фактах знал уже Аристотель, который в своей не дошедшей до нас книге Физические проблемы высказывал неудовлетворённость теорией концентрических сфер. Автолик из Питаны попытался преодолеть эти недостатки, но безуспешно.

Другим недостатком теории гомоцентрических сфер была её непрактичность: с её помощью было практически невозможно вычислять координаты планет.

По этим причинам теория гомоцентрических сфер уступила место более совершенной теории — теории эпициклов, с которой и связаны основные успехи математической астрономии античности (Гиппарх, II век до н. э., Птолемей, II век н. э.).

Начиная с поздней античности и особенно в средневековье и даже в эпоху Возрождения сильным доводом в пользу этой теории гомоцентрических сфер было её соответствие философии Аристотеля. Знаменитый философ Аверроэс призывал отказаться от теории Птолемея в пользу Аристотеля. Различные модификации теории концентрических сфер создавались на протяжении всего средневековья и эпохи Возрождения: ал-Битруджи, XII век[8], Региомонтан, XV век[9], Джиованни Баттиста Амико, XVI век[10], Джироламо Фракасторо, XVI век[11]. Однако успехи теоретической и наблюдательной астрономии посткопериканского периода привели к тому, что теория гомоцентрических сфер перестала восприниматься всерьёз, а вскоре (в XVII веке) была оставлена и сама геоцентрическая система мира.

1. Нейгебауер 1968, с. 179; Heath 1913, p. 202—207.
2. Evans 1998, p. 309.
3. Веселовский 1974, Yavetz 1998, 2001.
4. Mendell 2000, p. 109—111.
5. Heath 1913, pp. 212—216; Mendell 1998.
6. О Небе, книга II, глава 9. Online
7. Метафизика, книга XII, глава 8. Online
8. Рожанская 1976.
9. Shank 1998, Swerdlow 1999.
10. Swerdlow 1972.
11. di Bono 1996.

• Астрономия Древней Греции
• Геоцентрическая система мира
• История развития представлений о Вселенной

• Аристотель. «Метафизика», кн. XII, гл. 8.
• Симпликий. Комментарий к четырем книгам трактата Аристотеля «О небе». Комментарий ко второй книге (пер. и коммент. А.А.Россиуса)
• Models for planetary motion: from the homocentric spheres to epicycles and heliocentric orbits (Mogi Vicentini: 3D grapics and videos).
• C.S. McConnell. Models of Planetary Motion from Antiquity to the Renaissance
• H. Mendell. Eudoxos of Knidos (Eudoxus of Cnidus): astronomy and homocentric spheres
• Eudoxus explained by Geomag

• И. Н. Веселовский, Очерки по истории теоретической механики. М.: Высшая школа, 1974.
• С. В. Житомирский, Античная астрономия и орфизм. М.: Янус-К, 2001.
• О. Нейгебауер, Точные науки в древности. М.: Наука, 1968. [www.astro-cabinet.ru/library/Neigebauer/N_Ogl.htm Online]
• М. М. Рожанская, Механика на средневековом Востоке. М.: Наука, 1976.
• И. Д. Рожанский, История естествознания в эпоху эллинизма и Римской империи. М.: Наука, 1988.
• А. А. Россиус. Учение о гомоцентрических сферах в разных античных его вариантах по Симпликию. Историко-философский ежегодник 2004. М.: Наука, 2005. С. 5-10. Online
• E. J. Aiton, Celestial spheres and circles. History of Science, Vol. 19, pp. 76–114, 1981. Online
• V. di Bono, Copernicus, Amico, Fracastoro and Tusi’s Device: Observations on the Use and Trasmission of a Model. Journal for the History of Astronomy, V. 26, p. 133, 1995. Online
• J. L. E. Dreyer, History of the planetary systems from Thales to Kepler. Cambridge University Press, 1906. PDF
• J. Evans, The History and Practice of Ancient Astronomy. New York: Oxford University Press, 1998.
• A. Gregory, Eudoxus, Callippus and the Astronomy of the Timaeus. In Ancient Approaches to Plato's Timaeus, ed. Sharples, R. W. and A. Sheppard, pp. 5–28. London: Institute of Classical Studies. PDF
• T. L. Heath, Aristarchus of Samos, the ancient Copernicus: a history of Greek astronomy to Aristarchus. Oxford, Clarendon, 1913; reprinted New York, Dover, 1981. PDF
• C. M. Linton, From Eudoxus to Einstein: A history of mathematical astronomy. Cambridge University Press, 2004.
• H. Mendell, Reflections on Eudoxus, Callippus and their Curves: Hippopedes and Callippopedes. Centaurus, vol. 40, No. 3-4, pp. 177–275, 1998.
• R. C. Riddel, Eudoxan Mathematics and the Eudoxan Spheres. Arch. Hist. Exact Sci., V. 20, pp. 1–19, 1979. Статья на сайте журнала (недоступная ссылка)
• M. H. Shank, Regiomontanus and Homocentric Astronomy. Journal for the History of Astronomy, V. 29, p. 157, 1998. Online
• N. M. Swerdlow, Aristotelian Planetary Theory in the Renaissance: Giovanni Battista Amico’s homocentric sphere. Journal for the History of Astronomy, V. 3, p. 36, 1972. Online
• N. M. Swerdlow, Regiomontanus’s Concentric-sphere Models for the Sun and Moon. Journal for the History of Astronomy, V. 30, p. 1, 1999. Online
• H. Thurston, Early astronomy. New York, Springer-Verlag: 1994.
• L. Wright, The astronomy of Eudoxus: geometry or physics? Stud. Hist. and Phil. Sci., V. 4, pp. 165–172, 1973. Online
• I. Yavetz, On the homocentric spheres of Eudoxus, Arch. Hist. Exact Sci. V. 52, pp. 221–278, 1998. Статья на сайте журнала (недоступная ссылка)
• I. Yavetz, A New Role for the Hippopede of Eudoxus, Arch. Hist. Exact Sci. V. 56, pp. 69–93, 2001. Статья на сайте журнала (недоступная ссылка)
• I. Yavetz, Eudoxus and his Medieval Successors, ISF Research Workshop, "The Jews and the Sciences of the Stars", 2-4.02.2010, Bar Ilan University, Tel-Aviv.