Максимальное независимое множество
В теории графов максимальным независимым множеством, максимальным устойчивым множеством, или максимальным стабильным множеством называется независимое множество, не являющееся подмножеством другого независимого множества. То есть это такое множество вершин S, что любое ребро графа имеет хотя бы одну конечную вершину, не принадлежащую S, и любая вершина не из S имеет хотя бы одну соседнюю в S. Максимальное независимое множество является также доминирующим в графе, а любое доминирующее множество, являющееся независимым, должно быть максимальным независимым, поэтому максимальные независимые множества также называют независимыми доминирующими множествами. Граф может иметь много максимальных независимых множеств в широком диапазоне размеров.[1]

Самое большое по размеру максимальное независимое множество называется наибольшим независимым множеством.
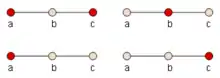
Например, в графе P3, пути с тремя вершинами a, b и c и двумя рёбрами ab и bc, множества {b} и {a,c} оба являются максимальными независимыми, из них только {a,c} является наибольшим независимым. Множество {a} независимо, но не максимальное, поскольку является подмножеством {a,c}. В этом же графе максимальными кликами являются множества {a,b} и {b,c}.
Словосочетание «максимальное независимое множество» употребляется также для описания максимальных подмножеств независимых элементов в математических структурах, отличных от графов, в частности, в векторных пространствах и матроидах.
Связь с другими множествами вершин
Если S — максимальное независимое множество в некотором графе, то оно является максимальной кликой в дополнении графа. Максимальная клика — это множество вершин, которые порождают полный подграф, и оно не содержится в большем полном подграфе. Таким образом, это множество вершин S, таких, что любая пара вершин в S соединена ребром, а для любой вершины не из S отсутствует ребро, соединяющее её с хотя бы одной вершиной в S. Граф может иметь несколько максимальных клик различного размера. Поиск максимальной клики максимального размера — это задача о максимальной клике.
Некоторые авторы в определении требуют, чтобы клика была максимальной, и употребляют термин клика вместо максимальная клика.
Дополнение максимального независимого множества, то есть вершины, не принадлежащие независимому множеству, образуют минимальное покрытие вершин. То есть дополнение — это вершинное покрытие, множество вершин, содержащих по меньшей мере одну конечную вершину любого ребра, и минимальное в том смысле, что ни одну из вершин нельзя удалить, не нарушив покрытия. Минимальное покрытие вершин изучается в статистической механике в модели газовой решётки на жёстких сферах, математической абстракции перехода из жидкости в твёрдое состояние.[2]
Любое максимальное независимое множество является доминирующим, то есть таким множеством вершин, что любая вершина в графе либо принадлежит множеству, либо смежна ему. Множество вершин является максимальным независимым множеством в том и только в том случае, когда оно является независимым доминирующим множеством.
Использование в характеристиках семейств графов
Некоторые семейства графов можно описать в терминах их максимальных клик или максимальных независимых множеств. Примеры включают графы с несводимыми максимальными кликами и графы с наследственно несводимыми максимальными кликами. Говорят, что граф имеет несводимые максимальные клики, если любая максимальная клика содержит ребро, которое не принадлежит никакой другой максимальной клике, и наследственно несводимые максимальные клики, если это свойство верно для любого подграфа.[3] Графы с наследственно несводимыми максимальными кликами включают графы без треугольников, двудольные графы и интервальные графы.
Кографы можно описать как графы, в которых любая максимальная клика пересекается с любым максимальным независимым множеством, и в которых это свойство верно для всех порождённых подграфов.
Оценки числа множеств
Мун и Мозер (Moon, Moser 1965) показали, что любой граф с n вершинами имеет не более 3n/3 максимальных клик. Также граф с n вершинами имеет не более 3n/3 максимальных независимых множеств. Граф, имеющий ровно 3n/3 максимальных независимых множеств, легко построить, просто взяв несвязный набор n/3 треугольных графов. Любое максимальное независимое множество в этом графе образуется выбором одной вершины из каждого треугольника. Дополнительный граф с 3n/3 максимальными кликами — это графы Турана специального вида. Ввиду связи этого графа с границей Муна и Мозера эти графы иногда называют графами Муна-Мозера. Более сильные границы возможны, если ограничен размер максимальных независимых множеств — число максимальных независимых множеств размера k в любом графе с n вершинами не превосходит
Графы, достигающие этой границы — это снова графы Турана.[4]
Некоторые семейства графов могут, однако, иметь существенно более сильные границы на число максимальных независимых множеств или максимальных клик. Например, если графы в семействе имеют O(n) рёбер, и семейство замкнуто относительно подграфов, то все максимальные клики имеют постоянный размер и число максимальных клик почти линейно.[5]
Ясно, что любой граф с несводимыми максимальными кликами имеет максимальных клик не больше, чем рёбер. Более сильная граница возможна для интервальных графов и хордальных графов — в этих графах не может быть более n максимальных клик.
Число максимальных независимых множеств в циклах с n вершинами задаётся числами Перрина, а число максимальных независимых множеств в пути с n вершинами задаётся последовательностью Падована.[6] Таким образом, обе эти последовательности пропорциональны степени 1.324718 (то есть пластического числа).
Алгоритмы перечисления множеств
Алгоритм для перечисления всех максимальных независимых множеств или максимальных клик в графе может быть использован как подпрограмма для решения многих NP-полных задач теории графов. Самые очевидные задачи — это задача о максимальном независимом множестве, задача о максимальной клике и минимальном независимом доминирующем множестве.
Все они должны быть максимальными независимыми множествами или максимальными кликами и могут быть найдены с помощью алгоритма, который перечисляет все такие множества и выбирает множество максимального или минимального размера. Таким же образом минимальное вершинное покрытие можно найти как дополнение одного из максимальных независимых множеств. Лоулер (Lawler 1976) заметил, что перечисление максимальных независимых множеств можно использовать также для поиска раскраски графа в 3 цвета — граф можно раскрасить в три цвета тогда и только тогда, когда дополнение одного из максимальных независимых множеств является двудольным. Он использовал этот подход не только для раскрашивания в 3 цвета, но и как часть более общего алгоритма раскраски графов, и похожий подход для раскраски графа был использован другими авторами.[7]
Другие более сложные задачи можно свести к поиску клики или независимого множества специального вида. Это даёт мотивацию для поиска алгоритмов, эффективно перечисляющих все максимальные независимые множества (или, что эквивалентно, максимальные клики).
Возможно напрямую превратить доказательство Муна и Мозера границы 3n/3 числа максимальных независимых множеств в алгоритм, который перечисляет все такие множества за время O(3n/3).[8] Для графов, имеющих максимально возможное число максимальных независимых множеств, этот алгоритм даёт постоянное время на одно найденное множество. Однако алгоритм с этой временной границей может быть крайне неэффективен для графов с более ограниченными количествами независимых множеств. По этой причине многие исследоватили ищут алгоритмы перечисления всех максимальных независимых множеств с полиномиальным временем на одно найденное множество.[9] Время нахождения одного максимального независимого множества пропорционально времени умножения матриц в плотных графах или быстрее в различных классах разреженных графов.[10]
Замечания
- Эрдёш (Erdős 1966) показал, что число различных размеров максимальных независимых множеств в графе с n вершинами может достигать и никогда не больше .
- Weigt, Hartmann, 2001.
- Information System on Graph Class Inclusions: графы с несводимыми максимальным кликами Архивировано 9 июля 2007 года. и с наследственно несводимыми максимальными кликами Архивировано 8 июля 2007 года..
- (Byskov 2003). Для более ранних работ смотрите (Croitoru 1979) и (Eppstein 2003).
- (Chiba, Nishizeki 1985). Условие разреженности эквивалентно условию, что семейство графов имеет ограниченную древесность.
- (Bisdorff, Marichal 2007); (Euler 2005); (Füredi 1987).
- (Eppstein 2003); (Byskov 2003).
- (Eppstein 2003). Для границ широко используемого алгоритма Брона — Кербоша смотрите (Tomita, Tanaka, Takahashi 2006).
- (Bomze, Budinich, Pardalos, Pelillo 1999); (Eppstein 2005); (Jennings, Motycková 1992); (Johnson, Yannakakis, Papadimitriou 1988); (Lawler, Lenstra, Rinnooy Kan 1980); (Liang, Dhall, Lakshmivarahan 1991); (Makino, Uno 2004); (Mishra, Pitt 1997); (Stix 2004); (Tsukiyama, Ide, Ariyoshi, Shirakawa 1977); (Yu, Chen 1993).
- (Makino, Uno 2004); (Eppstein 2005).
Ссылки
- R. Bisdorff, J.-L. Marichal. Counting non-isomorphic maximal independent sets of the n-cycle graph. — 2007. — arXiv:math.CO/0701647..
- I. M. Bomze, M. Budinich, P. M. Pardalos, M. Pelillo. Handbook of Combinatorial Optimization. — Kluwer Academic Publishers, 1999. — Т. 4. — С. 1—74..
- J. M. Byskov. Proceedings of the Fourteenth Annual ACM-SIAM Symposium on Discrete Algorithms. — 2003. — С. 456—457..
- N. Chiba, T. Nishizeki. Arboricity and subgraph listing algorithms // SIAM J. on Computing. — 1985. — Т. 14, вып. 1. — С. 210—223. — doi:10.1137/0214017..
- C. Croitoru. Proc. Third Coll. Operations Research. — Babeş-Bolyai University, Cluj-Napoca, Romania, 1979. — С. 55—60..
- D. Eppstein. Small maximal independent sets and faster exact graph coloring // Journal of Graph Algorithms and Applications. — 2003. — Т. 7, вып. 2. — С. 131—140. — arXiv:cs.DS/cs.DS/0011009.
- D. Eppstein. Proc. Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms. — 2005. — С. 451—459. — arXiv:cs.DS/0407036..
- P. Erdős. On cliques in graphs // Israel J. Math.. — 1966. — Т. 4, вып. 4. — С. 233—234. — doi:10.1007/BF02771637..
- R. Euler. The Fibonacci number of a grid graph and a new class of integer sequences // Journal of Integer Sequences. — 2005. — Т. 8, вып. 2. — С. 05.2.6..
- Z. Füredi. The number of maximal independent sets in connected graphs // Journal of Graph Theory. — 1987. — Т. 11, вып. 4. — С. 463—470. — doi:10.1002/jgt.3190110403..
- E. Jennings, L. Motycková. Proc. First Latin American Symposium on Theoretical Informatics. — 1992. — Т. 583. — С. 281—293.
- D.S. Johnson, M. Yannakakis, C. H. Papadimitriou. On generating all maximal independent sets // Information Processing Letters. — 1988. — Т. 27, вып. 3. — С. 119—123. — doi:10.1016/0020-0190(88)90065-8..
- E. L. Lawler. A note on the complexity of the chromatic number problem // Information Processing Letters. — 1976. — Т. 5, вып. 3. — С. 66—67. — doi:10.1016/0020-0190(76)90065-X..
- E. L. Lawler, J. K. Lenstra, A. H. G. Rinnooy Kan. Generating all maximal independent sets: NP-hardness and polynomial time algorithms // SIAM Journal on Computing. — 1980. — Т. 9, вып. 3. — С. 558—565. — doi:10.1137/0209042..
- J. Y.-T. Leung. Fast algorithms for generating all maximal independent sets of interval, circular-arc and chordal graphs // Journal of Algorithms. — 1984. — Т. 5. — С. 22—35. — doi:10.1016/0196-6774(84)90037-3..
- Y. D. Liang, S. K. Dhall, S. Lakshmivarahan. Proc. Symp. Applied Computing. — 1991. — С. 465—470.
- K. Makino, T. Uno. Proc. Ninth Scandinavian Workshop on Algorithm Theory. — Springer-Verlag, 2004. — Т. 3111. — С. 260—272. — (Lecture Notes in Compute Science)..
- N. Mishra, L. Pitt. Proc. Tenth Conf. Computational Learning Theory. — 1997. — С. 211—217. — ISBN 0-89791-891-6. — doi:10.1145/267460.267500..
- J. W. Moon, L. Moser. On cliques in graphs // Israel Journal of Mathematics. — 1965. — Т. 3. — С. 23—28. — doi:10.1007/BF02760024..
- V. Stix. Finding all maximal cliques in dynamic graphs // Computational Optimization Appl.. — 2004. — Т. 27, вып. 2. — С. 173—186. — doi:10.1023/B:COAP.0000008651.28952.b6.
- E. Tomita, A. Tanaka, H. Takahashi. The worst-case time complexity for generating all maximal cliques and computational experiments. — 2006. — Т. 363, вып. 1. — С. 28—42. — doi:10.1016/j.tcs.2006.06.015..
- S. Tsukiyama, M. Ide, H. Ariyoshi, I. Shirakawa. A new algorithm for generating all the maximal independent sets // SIAM J. on Computing. — 1977. — Т. 6, вып. 3. — С. 505—517. — doi:10.1137/0206036..
- Martin Weigt, Alexander K. Hartmann. Minimal vertex covers on finite-connectivity random graphs: A hard-sphere lattice-gas picture // Phys. Rev. E. — 2001. — Т. 63, вып. 5. — С. 056127. — doi:10.1103/PhysRevE.63.056127. — arXiv:cond-mat/0011446..
- C.-W. Yu, G.-H. Chen. Generate all maximal independent sets in permutation graphs // Internat. J. Comput. Math.. — 1993. — Т. 47. — С. 1—8. — doi:10.1080/00207169308804157..