Диаграмма Юнга
Диаграммы Юнга — наглядный способ описания представлений симметрических и полных линейных групп и изучения их свойств.
История
Диаграммы Юнга были предложены Альфредом Юнгом, математиком из Кембриджского университета, в 1900 году[1][2]. Впоследствии в 1903 году они были использованы Георгом Фробениусом для изучения симметрических групп.
Дальнейшее развитие диаграмм Юнга прослеживается в работах многочисленных математиков — таких, как Перси Макмэхон, Вильям Ходж, Гилберт Робинсон, Жан-Карло Рота, Ален Ласку и Марсель-Поль Шутценбергер .
Определения
Примечание: в этой статье для диаграмм и таблиц используется способ записи, принятый в англоязычных странах.
Диаграммы
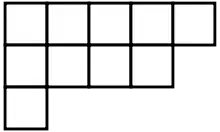
Диаграмма Юнга (также называемая диаграммой Ферре в случаях, когда вместо ячеек используют точки[3]) — это конечный набор ячеек или клеток, выровненных по левой границе, в котором длины строк образуют невозрастающую последовательность (каждая строка такой же длины как предыдущая, или короче). Набор чисел, состоящий из длин строк, задаёт разбиение λ неотрицательного целого числа n, которое равно общему количеству ячеек диаграммы. Аналогично, про конкретно взятое разбиение λ говорят, что оно задаёт форму соответствующей диаграммы Юнга.
Включение одной диаграммы Юнга в другую задаёт частичный порядок на множестве всех разбиений, что, в свою очередь, задаёт структуру, называемую решеткой Юнга.
Разбиение, задаваемое транспонированной диаграммой Юнга, называется разбиением, сопряжённым или транспонированным к λ.
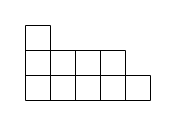
Общепринято обозначать клетки, используя пару целых чисел, первое из которых соответствует номеру строки в диаграмме, а второе — номеру столбца в этой строке. Тем не менее, существуют два различных соглашения о том, как диаграммы изображать: либо располагать строки следующая под предыдущей, либо наоборот. Первое обычно используется среди англоговорящих, в то время как второе — среди франкоговорящих, поэтому в шуточной терминологии эти соглашения носят названия английской нотации и французской нотации соответственно. Например, в своей книге о симметрических функциях Макдональд рекомендует читателям, предпочитающим французскую нотацию, «читать книгу вверх ногами в зеркале»[4].
Английская нотация соответствует общепринятой для нумерации элементов матриц, а французская ближе к соглашению об обозначении декартовых координат (хотя для диаграмм Юнга вертикальная координата всё же первая). Рисунок справа в английской нотации изображает диаграмму Юнга разбиения (5, 4, 1). Сопряжённое разбиение, измеряющее высоты столбцов, есть (3, 2, 2, 2, 1).
Таблицы
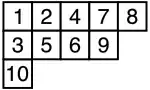
Таблицей Юнга называется диаграмма Юнга, клетки которой заполнены символами из какого-нибудь алфавита, который обычно предполагается вполне упорядоченным множеством. Изначально, алфавитом полагалось множество пронумерованных переменных x1, x2, x3…, но в настоящее время, для краткости, чаще используются натуральные числа. В их классическом применении к теории представлений симметрических групп, таблицы Юнга заполнены n различными числами, произвольно вписанными в клетки диаграммы. Таблица называется стандартной, если числа возрастают в каждой строчке и в каждом столбце. Число различных стандартных таблиц Юнга с n элементами описывается числом инволюций в симметрической группе порядка n:
В других приложениях бывает естественным разрешить повторения некоторых чисел (а какие-то не использовать вовсе). Таблица называется полустандартной, если числа не убывают по горизонтали и возрастают по вертикали. Выписывая, сколько раз каждое число появилось в таблице, мы получаем последовательность, известную как вес таблицы. Поэтому стандартные таблицы Юнга в точности совпадают с полустандартными таблицами веса (1,1,…,1).
Вариации
Существуют вариации определения таблицы: например, в «строчно-строгой» таблице числа строго возрастают вдоль строк, и не возрастают вдоль столбцов. Таблицы с убывающими числами рассматриваются в теории плоских разбиений. Существуют и другие обобщения (domino tableaux, ribbon tableaux), где клеточки могут объединяться до того, как им назначают числа.
Косые таблицы Юнга
Косая форма — это пара разбиений (λ,μ), такая что диаграмма Юнга для λ содержит диаграмму для μ; обозначение: λ/μ. Если λ=(λ1,λ2,…) и μ=(μ1,μ2,…), то вложение диаграмм означает, что μi ≤ λi для всех i. Косая диаграмма косой формы λ/μ — это теоретико-множественная разность диаграмм для λ и для μ: множество квадратов, принадлежащих диаграмме для λ, но не принадлежащих диаграмме для μ. Косая таблица формы λ/μ получается посредством заполнения клеток соответствующей косой диаграммы; такая таблица называется полустандартной, если числа не убывают по строкам и возрастают по столбцам; полустандартная таблица называется стандартной, если каждое число от единицы до количества клеток встречается ровно один раз. В то время как отображение из разбиений в их диаграммы Юнга является инъективным, то же самое не верно для отображения из косых форм в косые диаграммы;[5] Хотя многие свойства косых таблиц зависят только от заполненных квадратов, некоторые могут зависеть и от косой формы. Таблицы Юнга могут быть отождествлены с косыми таблицами, для которых разбиение μ пустое (разбиение нуля).
Любая косая полустандартная таблица T формы λ/μ, заполненная положительными целыми числами, порождает последовательность разбиений (или последовательность диаграмм Юнга): первый элемент — это μ, а i-й получается добавлением всех ячеек, содержащих число, меньшее или равное i; в конце концов получается диаграмма λ. Любая пара соседних форм в этой последовательности образует косую форму, в каждом столбце которой не более одной ячейки; такие формы называются горизонтальными полосками. Эта последовательность полностью определяет таблицу T, и иногда в литературе (например, в книге Макдональда) косые полустандартные формы определяют как последовательности такого вида.
Приложения
Диаграммы Юнга находят многочисленные применения в комбинаторике, теории представлений и алгебраической геометрии. Были исследованы различные способы подсчёта числа диаграмм, которые привели к определению и формулам для многочленов Шура. Известно множество алгоритмов, выполняемых непосредственно на диаграммах, такие как jeu de taquin («игра в пятнашки») Шютценбергера и соответствие Робинсона — Шенстеда — Кнута. Ласку и Шютценбергер изучили ассоциативное произведение на множестве полустандартных диаграмм Юнга, приводящее в итоге к структуре, известной как плактический моноид.
В теории представлений, стандартные таблицы Юнга размера k описывают базисы неприводимых представлений симметрической группы Sk. Стандартный мономиальный базис в конечномерном неприводимом представлении полной линейной группы GLn параметризуется множеством полустандартных таблиц Юнга фиксированной формы над алфавитом {1, 2, …, n}. Из этого факта вытекает несколько важных следствий для теории инвариантов, начиная с работ Ходжа по однородным координатным кольцам грассманианов, за которыми последовали работы Айзенбада и Жан-Карло Роты, вместе с соавторами де Кончини и Прочези. Правило Литтлвуда — Ричардсона, описывая (среди прочего) разложение тензорного произведения неприводимых представлений GLn на неприводимые компоненты, формулируется в терминах определённых косых полустандартных таблиц.
Приложения в алгебраической геометрии сосредоточены вокруг исчисления Шуберта на грассманианах и многообразиях флагов. Некоторые важные классы когомологий могут быть представлены с помощью многочленов Шуберта и описаны в терминах диаграмм Юнга.
Приложения в теории представлений
Диаграммы Юнга находятся во взаимно однозначном соответствии с неприводимыми представлениями симметрической группы (над комплексными числами). Они предоставляют удобный способ задания симметризаторов Юнга, на которых строится теория представлений симметрической группы. Многие факты о представлениях могут быть выведены из соответствующих диаграмм. Ниже приведены два примера: определение размерности представления и ограниченные представления.
Диаграммы Юнга также параметризуют неприводимые полиномиальные представления полной линейной группы GLn (когда они содержат не более n непустых строк), а также неприводимые представления специальной линейной группы SLn (когда они содержат не более n − 1 непустых строк) и неприводимые комплексные представления специальной унитарной группы SUn (опять же, когда они содержат не более n − 1 непустых строк). В этих случаях центральную роль играют полустандартные таблицы с числами, не превосходящими n (в частности, их число определяет размерность представлений).
Формула крюков
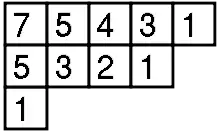
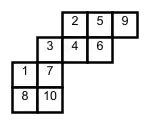
Размерность неприводимого представления πλ (отвечающего разбиению λ числа n) симметрической группы Sn равняется количеству различных стандартных таблиц Юнга, соответствующим диаграмме разбиения. Это число может быть посчитано по формуле крюков.
Длиной крюка hook(x) клетки x в диаграмме Y(λ) формы λ называется число клеток в той же строке правее плюс число клеток в том же столбце ниже плюс один (сама клетка). По формуле крюков, размерность неприводимого представления равняется n!, поделённому на произведение длин всех крюков диаграммы:
Рисунок справа иллюстрирует длины крюков для диаграммы разбиения 10 = 5 + 4 + 1. Поэтому
Аналогично, размерность неприводимого представления W(λ) группы GLr, отвечающее разбиению λ числа n (на не более чем r слагаемых), равна количеству полустандартных таблиц формы λ (содержащих только числа от 1 до r), которое даётся формулой:
где индекс i нумерует строку, а индекс j нумерует столбец клетки.[6] Например, разбиение (5,4,1) порождает размерность соответствующего неприводимого представления группы GL7 (обход клеток построчный):
Ограниченные представления
Представление симметрической группы Sn на n элементах является также представлением симметрической группы на n − 1 элементе, Sn−1. Однако неприводимое представление Sn не обязательно является неприводимым представлением Sn−1, а может быть прямой суммой нескольких таких представлений. Эти представления называются факторами ограниченного представления.
Вопрос определения разложения ограниченного представления данного неприводимого представления Sn, отвечающего разбиению λ числа n, имеет следующий ответ. Рассматриваются все диаграммы Юнга, которые можно получить из диаграммы формы λ удалением одной клетки (которая должна находиться в конце своей строки и своего столбца). Ограниченное представление тогда разлагается в прямую сумму неприводимых представлений Sn−1, соответствующих этим диаграммам, причём каждое из них в сумме встречается ровно один раз.
См. также
Примечания
- Кнут, Дональд Э. (2005), Искусство программирования, Том 3: Сортировка и поиск (2ое ed.), Вильямс, Addison-Wesley, с. 66.
- Young, A. (1900), On quantitative substitutional analysis, Proceedings of the London Mathematical Society, Ser. 1 Т. 33 (1): 97–145, DOI 10.1112/plms/s1-33.1.97. См., в частности, стр. 133.
- Р. Стенли Перечислительная комбинаторика. М: Мир, 1990. с. 52.
- Macdonald, 1979, p. 2.
- например, косая диаграмма, состоящая из единственного квадрата в позиции (2,4) может быть получена путём удаления поддиаграммы μ из диаграммы λ = (5,4,2,1), или ещё бесконечным количеством способов. Вообще говоря, любая косая диаграмма, для которой множество непустых строк (или непустых столбцов) не является сплошным, или не содержащая первой строки (или первого столбца), происходит более чем из одной косой формы.
- Predrag Cvitanović. Group Theory: Birdtracks, Lie's, and Exceptional Groups (англ.). — Princeton University Press, 2008., ур. 9.28 и приложение B.4
Литература
- Берштейн М. А., Мерзон Г. А. . Диаграммы Юнга, пути на решётке и метод отражений. — Препринт. Архивная копия от 15 апреля 2015 на Wayback Machine
- Буфетов А. И., Житлухин М. М., Н. Е. Козин Н. Е. . Диаграммы Юнга и их предельная форма. — М.: Изд-во МЦНМО, 2013. — ISBN 978-5-4439-0077-3.
- Смирнов Е. Ю. . Диаграммы Юнга, плоские разбиения и знакочередующиеся матрицы. — М.: Изд-во МЦНМО, 2014. — ISBN 978-5-4439-0137-4.
- Фултон, Уильям. . Таблицы Юнга и их приложения к теории представлений и геометрии = Young Tableaux With Application to Representation Theory and Geometry. — М.: Изд-во МЦНМО, 2006. — ISBN 5-94057-165-4.
- Cvitanović, Predrag. . Group Theory: Birdtracks, Lie’s, and Exceptional Groups. — Princeton: Princeton University Press, 2008.
- Fulton, William; Harris, Joe. . Representation theory. A first course. — New York: Springer-Verlag, 1991. — (Graduate Texts in Mathematics. Readings in Mathematics, vol. 129). — ISBN 978-0-387-97495-8. (Lecture 4)
- Georgi, Howard. . Lie Algebras in Particle Physics, 2nd edition. — Westview.
- Macdonald I. G. . Symmetric functions and Hall polynomials (англ.). — Oxford: The Clarendon Press, Oxford University Press, 1979. — viii + 180 p. — (Oxford Mathematical Monographs). — ISBN 0-19-853530-9. MR: 84g:05003
- Manivel, Laurent. . Symmetric Functions, Schubert Polynomials, and Degeneracy Loci. — American Mathematical Society.
- Novelli, Jean-Christophe; Pak, Igor; Stoyanovkii, Alexander V. . A direct bijective proof of the Hook-length formula. — Discrete Mathematics and Theoretical Computer Science, 1997, 1. — P. 53—67.
- Sagan, Bruce E. . The Symmetric Group. — Springer, 2001. — ISBN 0-387-95067-2.
- Vinberg E. B. . Young tableau // Hazewinkel, Michiel. Encyclopedia of Mathematics. — Springer, 2001. — ISBN 978-1-55608-010-4.
- Yong, Alexander. . What is...a Young Tableau?. — Notices of the American Mathematical Society, 2007, 54 (2). — P. 240—241.
Ссылки
- Буфетов А. И., Козин Н. Е. Диаграммы Юнга, ортогональные полиномы и случайные матрицы // Летняя школа «Современная математика», 2010. 19 июля 2010 г. 15:30, г. Дубна
- Weisstein, Eric W. Ferrers Diagram // MathWorld—A Wolfram Web Resource.
- Weisstein, Eric W. Young Tableau // MathWorld—A Wolfram Web Resource.
- Semistandard tableaux entry in the FindStat database
- Standard tableaux entry in the FindStat database