Биэллиптическая переходная орбита
Биэллиптическая переходная орбита — в космонавтике и аэрокосмической технике орбита манёвра, при котором космический аппарат переходит с одной орбиты на другую. В некоторых случаях биэллиптический переход требует меньшей характеристической скорости дельта-v, чем перелёт по гомановскому эллипсу.
Биэллиптическая орбита состоит из двух половин эллиптических орбит. Сначала космическому аппарату, находящемуся на начальной орбите, придаётся определённая дельта-v для перехода на первую часть биэллиптической орбиты с апоцентром в некоторой точке на расстоянии от центрального тела. В этой точке аппарату также придаётся некоторая дельта-v для перехода на второй участок биэллиптической орбиты с перицентром на расстоянии, равном радиусу итоговой желаемой орбиты. В точке перицентра в третий раз аппарату придаётся некоторая дельта-v, в результате аппарат переходит на требуемую орбиту.[1]
Биэллиптические перелёты обычно требуют больше топлива и времени, чем гомановские, но некоторые биэллиптические траектории требуют меньшей суммарной дельта-v, чем гомановская траектория, в случае отношения больших полуосей конечной и начальной траектории, превышающего 11,94, в зависимости от большой полуоси промежуточной орбиты.[2]
Идея биэллиптической переходной орбиты была впервые представлена в статье Ари Штернфельда в 1934 году.[3]
Вычисления
Дельта-v

Три значения изменения скорости можно получить непосредственно из интеграла энергий,
где
- — скорость аппарата на орбите,
- — гравитационный параметр притягивающего тела,
- — расстояние от притягивающего центра до тела на орбите,
- — большая полуось орбиты тела.
В рассматриваемой задаче
- — радиус начальной круговой орбиты,
- — радиус конечной круговой орбиты,
- — радиус общего апоцентра двух эллиптических участков переходной орбиты, свободный параметр манёвра,
- и равны большим полуосям эллиптических участков переходной орбиты, задаются равенствами
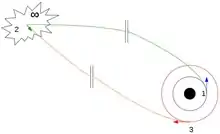
При старте с начальной круговой орбиты радиуса (тёмно-синяя окружность на рисунке), добавление скорости по направлению движения (вектор в положении 1 на рисунке) переводит космический аппарат на первый эллиптический участок орбиты перехода (бирюзовая линия). Величина необходимой дельта-v равна
Когда апоцентр первого эллиптического участка достигается на расстоянии , аппарату второй раз придаётся дополнительная скорость по направлению движения (вектор в положении 2 на рисунке), в результате на новой эллиптической орбите (оранжевая кривая) перицентр находится в точке касания итоговой круговой орбиты. Величина требуемой для перехода на эту часть переходной орбиты равна
Наконец, когда достагется финальная круговая орбита радиуса , аппарату придаётся вектор скорости против движения по орбите (вектор в положении 3 на рисунке) для перехода на итоговую круговую орбиту (красная окружность). Финальная добавка скорости равна
Если , то манёвр преобразуется в гомановскую траекторию (в этом случае равно нулю). Следовательно, биэллиптическая орбита представляет более общий тип траектории, чем гомановская.
Максимальная экономия в смысле добавочной скорости может быть вычислена в предположении , тогда полное значение принимает вид .
В таком случае переход называется бипараболическим, поскольку оба участка траектории являются не эллипсами, а параболами. Время перелёта также стремится к бесконечности.
Время перелёта
Как и в случае гомановского перелёта, обе части траектории, используемой в биэллиптическом перелёте, являются в точности половинами эллипсов. Это означает, что время, необходимое для преодоления каждой фазы перехода, является половиной орбитального периода для каждого эллипса.
Используем уравнение для орбитального периода и указанные выше обозначения:
Полное время перелёта является суммой промежутков времени для каждой из половин эллипсов, следовательно
Итоговый интервал времени:
Сравнение с гомановской траекторией
Дельта-v
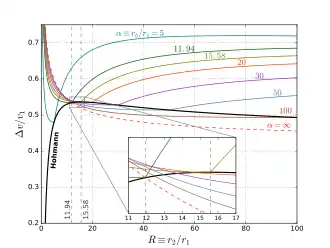
Рисунок показывает полное значение , требуемое для перехода с круговой орбиты радиуса на другую круговую орбиту радиуса . Величина нормирована на орбитальную скорость начальной орбиты, и представлена в виде функции отношения радиусов конечной и начальной орбиты ; таким образом, сопоставление величин является общим, не зависящим от и по отдельности, а только от их отношения.[2]
Чёрная кривая показывает значение для гомановской траектории, цветные кривые соответствуют биэллиптическим траекториям с различными значениями параметра , определённого как расстояние апоцентра биэллиптической орбиты, делённое на радиус начальной орбиты, и указанного рядом с кривыми. На врезке крупным планом показана область, где кривые для биэллиптических траекторий пересекают кривую для гомановской орбиты первый раз.
Можно заметить, что гомановский перелёт является более эффективным при отношении радиусов меньшем 11,94. С другой стороны, если радиус итоговой орбиты более чем в 15,58 раз превышает радиус начальной орбиты, то любой биэллиптический переход вне зависимости от апоцентрического расстояния (оно должно всё же превышать радиус итоговой орбиты) требует меньшую чем гомановская траектория. В области от 11,94 до 15,58 эффективность той или иной орбиты зависит от апоцентрического расстояния . Для заданного в этом диапазоне существует значение , выше которого предпочтительна биэллиптическая траектория и ниже которого предпочтительна гомановская траектория. В следующей таблице указаны значения для некоторых случаев.[4]
| Отношение радиусов орбит, | Минимум | Комментарий |
|---|---|---|
| 0 — 11,94 | - | Гомановский перелёт лучше |
| 11,94 | Бипараболическая траектория | |
| 12 | 815,81 | |
| 13 | 48,90 | |
| 14 | 26.10 | |
| 15 | 18,19 | |
| 15,58 | 15,58 | |
| более 15,58 | более | Любая биэллиптическая траектория лучше |
Время перелёта
Длительное время перелёта по биэллиптической орбите
является существенным недостатком такого орбитального манёвра. В случае бипараболической траектории время перелёта становится бесконечным.
Гомановский перелёт обычно требует меньше времени, поскольку движение происходит только по половине эллипса переходной орбиты:
Пример
Для перехода с низкой круговой орбиты радиуса r0 = 6700 км вокруг Земли на новую круговую орбиту радиуса r1 = 93 800 км при использовании гомановской траектории потребуется Δv, равное 2825,02 + 1308,70 = 4133;72 м/с. Поскольку r1 = 14r0 > 11,94r0, то биэллиптическая траектория позволит затратить меньшую Δv. Если космическому аппарату сначала придать дополнительную скорость 3061,04 м/с, переведя таким образом на эллиптическую орбиту с апогеем при r2 = 40r0 = 268 000 км, а затем в апогее придать ещё 608,825 м/с для достижения новой орбиты с перигеем на расстоянии r1 = 93 800 км, и в конце манёвра в перицентре второго участка переходной орбиты уменьшить скорость на 447,662 м/с, переведя аппарат на итоговую орбиту, то полное значение Δv будет равно 4117,53 м/с, что на 16,19 м/с (0,4 %) меньше, чем при гомановской траектории.
Уменьшение значения Δv можно усилить при увеличении промежуточного апогея, увеличив при этом время перелёта. Например, при апогее 75,8r0 = 507 688 км (в 1,3 раза превышает среднее расстояние от Земли до Луны) уменьшение Δv относительно гомановской траектории составит 1 %, но перелёт займёт 17 суток. В случае крайне большого расстояния в апоцентре, 1757r0 = 11 770 000 км (в 30 раз превышает среднее расстояние от Земли до Луны) экономия составит 2 % по сравнению с гомановской орбитой, но перелёт займёт 4,5 года (без учёта гравитационных возмущений от других тел Солнечной системы). Для сравнения, перелёт по гомановской траектории займёт 15 часов 34 минуты.
| Тип | Траектория Гомана | Биэллиптическая траектория | |||
|---|---|---|---|---|---|
| Апогей, км | 93 800 | 268 000 | 507 688 | 11 770 000 | ∞ |
| Добавка скорости 1 (м/с) | 2825,02 | 3061,04 | 3123,62 | 3191,79 | 3194,89 |
| Добавка скорости 2 (м/с) | 1308,70 | 608,825 | 351,836 | 16,9336 | 0 |
| Добавка скорости 3 (м/с) | 0 | −447,662 | −616,926 | −842,322 | −853,870 |
| Суммарное значение (м/с) | 4133,72 | 4117,53 | 4092,38 | 4051,04 | 4048,76 |
| Отношение | 100 % | 99,6 % | 99,0 % | 98,0 % | 97,94 % |
- Δv направлено в сторону движения
- (отрицательное значение) Δv направлено против движения
На биэллиптической орбите большая часть Δv передаётся в первый момент, что вносит большой вклад в орбитальную энергию тела.
Примечания
- Curtis, Howard. Orbital Mechanics for Engineering Students (англ.). — Elsevier, 2005. — P. 264. — ISBN 0-7506-6169-0.
- Vallado, David Anthony. Fundamentals of Astrodynamics and Applications (англ.). — Springer, 2001. — P. 318. — ISBN 0-7923-6903-3.
- Sternfeld, Ary J.[sic] (1934-02-12), Sur les trajectoires permettant d'approcher d'un corps attractif central à partir d'une orbite keplérienne donnée, Comptes rendus de l'Académie des sciences (Paris) Т. 198 (1): 711–713, <https://gallica.bnf.fr/ark:/12148/bpt6k31506/f711.image.langEN>
- Gobetz, F. W.; Doll, J. R. A Survey of Impulsive Trajectories (англ.) // AIAA Journal : journal. — American Institute of Aeronautics and Astronautics, 1969. — May (vol. 7, no. 5). — P. 801—834. — doi:10.2514/3.5231.
- Escobal, Pedro R. Methods of Astrodynamics. — New York: John Wiley & Sons, 1968. — ISBN 978-0-471-24528-5.