Алгоритм Ахо — Корасик

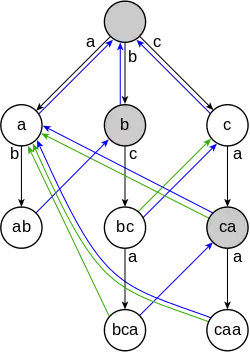
Недетерминированный автомат для словаря {a, ab, bc, bca, c, caa}. Серые вершины промежуточные, белые конечные. Синие стрелки — суффиксные ссылки, зелёные — конечные.

Алгоритм строит конечный автомат, которому затем передаёт строку поиска. Автомат получает по очереди все символы строки и переходит по соответствующим рёбрам. Если автомат пришёл в конечное состояние, соответствующая строка словаря присутствует в строке поиска.

Несколько строк поиска можно объединить в дерево поиска, так называемый бор (префиксное дерево). Бор является конечным автоматом, распознающим одну строку из ${\displaystyle m}$ — но при условии, что начало строки известно.

Первая задача в алгоритме — научить автомат «самовосстанавливаться», если подстрока не совпала. При этом перевод автомата в начальное состояние при любой неподходящей букве не подходит, так как это может привести к пропуску подстроки (например, при поиске строки aabab, попадается aabaabab, после считывания пятого символа перевод автомата в исходное состояние приведёт к пропуску подстроки — верно было бы перейти в состояние a, а потом снова обработать пятый символ). Чтобы автомат самовосстанавливался, к нему добавляются суффиксные ссылки, нагруженные пустым символом ⌀ (так что детерминированный автомат превращается в недетерминированный). Например, если разобрана строка aaba, то бору предлагаются суффиксы aba, ba, a. Суффиксная ссылка — это ссылка на узел, соответствующий самому длинному суффиксу, который не заводит бор в тупик (в данном случае a).

Для корневого узла суффиксная ссылка — петля. Для остальных правило таково: если последний распознанный символ — ${\displaystyle c}$, то осуществляется обход по суффиксной ссылке родителя, если оттуда есть дуга, нагруженная символом ${\displaystyle c}$, суффиксная ссылка направляется в тот узел, куда эта дуга ведёт. Иначе — алгоритм проходит по суффиксной ссылке ещё и ещё раз, пока либо не пройдёт по корневой ссылке-петле, либо не найдёт дугу, нагруженную символом ${\displaystyle c}$.

 * ···⌀···> * ···⌀···> * ···⌀···> *
 |                                |
 c                                c
 ↓                                ↓
[*] ·············⌀··············> *
     новая суффиксная ссылка

Этот автомат недетерминированный. Преобразование недетерминированного конечного автомата в детерминированный в общем случае приводит к значительному увеличению количества вершин. Но этот автомат можно превратить в детерминированный, не создавая новых вершин: если для вершины ${\displaystyle v}$ некуда идти по символу ${\displaystyle c}$, проходимся по суффиксной ссылке ещё и ещё раз — пока либо не попадём в корень, либо будет куда идти по символу ${\displaystyle c}$.

Всю детерминизацию удобно делать рекурсивно. Например, для суффиксной ссылки:

 алг СуффСсылка(v)
   если v.кэшСуффСсылка ≠ Ø      // для корня изначально корень.кэшСуффСсылка = корень
     вернуть v.кэшСуффСсылка
   u := v.родитель
   c := v.символ
   повторять
     u := СуффСсылка(u)
   до (u = корень) или (существует путь u —c→ w)
   если существует переход u —c→ w
     то v.кэшСуффСсылка := w
     иначе v.кэшСуффСсылка := корень
   вернуть v.кэшСуффСсылка

Детерминизация увеличивает количество конечных вершин: если суффиксные ссылки из вершины ${\displaystyle v}$ ведут в конечную ${\displaystyle u}$, сама ${\displaystyle v}$ тоже объявляется конечной. Для этого создаются так называемые конечные ссылки: конечная ссылка ведёт на ближайшую по суффиксным ссылкам конечную вершину; обход по конечным ссылкам даёт все совпавшие строки.

 алг ВывестиРезультат(v, i)
   напечатать "Найдено " + v.иголка + " в позиции " + (i - v.глубина + 1)

 алг ОсновнаяЧастьПоиска
   состояние := корень
   цикл i=1..|стогСена|
     состояние := Переход(состояние, стогСена[i]);
     если состояние.иголка ≠ Ø
       ВывестиРезультат(состояние, i)
     времСост := состояние
     пока КонечнаяСсылка(времСост) ≠ Ø
       времСост := КонечнаяСсылка(времСост);
       ВывестиРезультат(времСост, i)

Суффиксные и конечные ссылки в автомате можно рассчитывать по мере надобности уже на фазе поиска. Побочные переходы — можно вычислять на месте, никак не кэшируя, можно кэшировать для всех узлов, можно — для важнейших (на асимптотическую оценку алгоритма всё это не влияет).

Вычислительная сложность работы алгоритма зависит от организации данных. Например:

• Если таблицу переходов автомата хранить как индексный массив — расход памяти ${\displaystyle O(n\sigma )}$, вычислительная сложность ${\displaystyle O(n\sigma +H+k)}$, где ${\displaystyle H}$ — длина текста, в котором производится поиск, ${\displaystyle n}$ — общая длина всех слов в словаре, ${\displaystyle \sigma }$ — размер алфавита, ${\displaystyle k}$ — общая длина всех совпадений.
• Если таблицу переходов автомата хранить как красно-чёрное дерево — расход памяти снижается до ${\displaystyle O(n)}$, однако вычислительная сложность поднимается до ${\displaystyle O((H+n)\log \sigma +k)}$.

• https://xlinux.nist.gov/dads/HTML/ahoCorasick.html