Черви Патерсона
Черви Па́терсона (англ. Paterson's worms) — семейство клеточных автоматов типа тьюрмитов, придуманное в 1971 году британским учёным Майком Патерсоном (англ. Mike Paterson) для моделирования поведения и кормёжки некоторых доисторических червей. Несмотря на простой набор правил, поведение автоматов может быть очень сложным, и для одного из наборов правил его судьба неизвестна.
Предыстория

Доисторические черви кормились осадками на дне прудов и избегали повторного прохождения своих путей, поскольку там было мало еды. Однако еда встречалась кучками, поэтому они стремились держаться вблизи уже пройденных путей. При этом разным видам червей были свойственны различные правила, определяющие, насколько близко к пройденным путям держаться, когда и как резко поворачивать[1].
В 1969 году Дэвид Рауп (англ. David Raup) и Адольф Зейлахер создали компьютерную симуляцию ископаемых следов червей, что вдохновило Патерсона и Джона Конвея на поиск простых моделей клеточных автоматов для исследования идеализированных червей на решётке[2]. Конвей предлагал исследовать червей на квадратной решётке, однако там были всего три вида червей с довольно скучным поведением, а Патерсон предложил использовать треугольную решётку.
Описание
В этой модели червь ползает по треугольной решётке, грани которой изображают еду, и при прохождении грани она закрашивается («съедается»)[3]. В каждой вершине червь выбирает, вдоль какой грани направиться, исходя из того, какие из шести граней, примыкающих к вершине, закрашены. Направления отсчитываются с точки зрения червя[1]. Червь умирает, если в вершине нет незакрашенных («несъеденных») граней, что, впрочем, возможно только в начальном состоянии из соображений чётности[4].
Правила заданы заранее и определяют конкретный клеточный автомат в семействе («вид червя»), однако часто считается, будто червь принимает решение на каждом шаге, но если он уже сталкивался с подобной ситуацией, то обязан принять такое же решение.
Нумерация правил
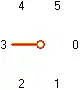
Правила могут быть классифицированы заданием направлений, которые червь выбирает, впервые «сталкиваясь» с незнакомой ситуацией, в порядке возникновения этих ситуаций. Направления обычно нумеруют по часовой стрелке, начиная с 0 — направления вперёд, см. изображение слева[5]. При этом червь не может выбрать направление 3 — повернуть назад. Также обычно не указываются выборы, которые червю не придётся сделать, поскольку он умирает раньше, и считается, что первый поворот червь делает вправо, поскольку случай левого поворота симметричен[1].
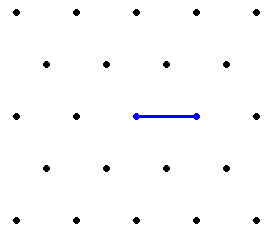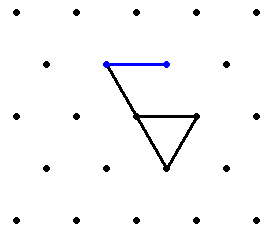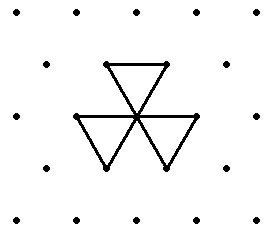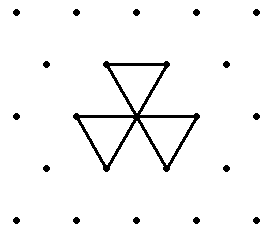
Например, правило {2, 0, 0}, задающее червя, изображённого справа, говорит, что при первом выборе (все 5 направлений незакрашены) червь поворачивает направо-назад, а при двух следующих (закрашено направление направо-назад и закрашены направления налево-вперёд, налево-назад и направо назад соответственно) выбирает движение прямо. Дальшейшие выборы не указаны, поскольку червь третий раз возвращается в начало и умирает. Если ограничиться случаями, в которых червь делает первый поворот направо, то потенциально существует 1296 возможных правил[6]. Однако с учётом того, что червь часто умирает, не успев осуществить все возможные выборы, а потому нет смысла отличать эти правила, их остаётся всего 412[4]. Среди них 336 конечны, 73 бесконечны и циклически повторяются со сдвигом, для двух бесконечность не доказана, но предполагается (это правила {1,0,4,2,0,2,0} и {1,0,4,2,0,1,5}), а поведение ещё одного неизвестно (правило {1,0,4,2,0,1,5})[4].
Примечания
- Beeler, Michael Paterson's Worm. Massachusetts Institute of Technology (июнь 1973). Дата обращения: 15 августа 2008.
- Paterson's Worms. WolframMathworld. Дата обращения: 15 августа 2008.
-
Hayes, Brian. In Search of the Optimal Scumsucking Bottomfeeder (англ.) // American Scientist : magazine. — Sigma Xi, the Scientific Research Society. — Vol. 95, no. 5. — P. 392—396. — doi:10.1511/2003.5.392.

- Chaffin, Benjamin Paterson's Worms. Архивировано 7 июня 2011 года.
- Pegg Jr., Ed Math Games: Paterson's Worms Revisited. MAA Online (27 октября 2003). Дата обращения: 15 августа 2008. Архивировано 23 марта 2004 года.
- Gardner, Martin (1986), Knotted doughnuts and other mathematical entertainments, W. H. Freeman, ISBN 978-0-7167-1799-7