Космический корабль (конфигурация клеточного автомата)
Косми́ческий кора́бль[5] (англ. spaceship) — класс конфигураций в «Жизни» — созданной Конвеем модели клеточного автомата.
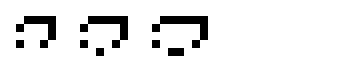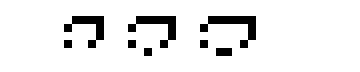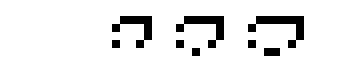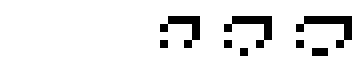
Описание
Конфигурация «Жизни» или другого клеточного автомата называется космическим кораблём, если через определённое количество поколений она вновь появляется без дополнений или потерь, но со смещением относительно исходного положения. Наименьшее такое число поколений — период космического корабля[6].
Первым обнаруженным космическим кораблём стал планер. Планер был найден во время отслеживания эволюции R-пентамино в 1970 году Ричардом Гаем[1][7][8].
Космический корабль периода p, который перемещается на (m,n) в течение его периода, где m ≥ n, имеет тип (m, n) / p. Как было доказано Конуэем в 1970 году, p ≥ 2m + 2n[6].
Космические корабли, движущиеся по горизонтали или вертикали, называются ортогональными кораблями. Если движение космического корабля происходит по диагонали под углом 45°, такой корабль называется диагональным. Космические корабли, движущиеся под другими углами, называются косыми или наклонными (англ. oblique). В 2010 году был сконструирован первый наклонный космический корабль типа (5120, 1024) / 33699586[9].
Скорость
Скоростью света в заданном клеточном автомате называют наибольшую скорость распространения информации. Скорость света в «Жизни» равна скорости перемещения шахматного короля — скорости в одну клетку за поколение по горизонтали, вертикали или диагонали. Обычно скорость света обозначается буквой c[1][6][10][11].
Скорость космического корабля определяется отношением расстояния смещения к периоду. Часто скорость выражается через c. Так, скорость планера в «Жизни» равна c / 4, так как он перемещается на одну клетку по диагонали за четыре поколения[7]. Простейший ортогональный космический корабль, ЛКК, движется со скоростью c / 2[2].
В общем случае, если космический корабль в двумерном клеточном автомате на квадратной сетке перемещается на вектор (x, y) через n поколений, его скорость равна[11]
Примеры
B3/S35
Следующие конфигурации являются ортогональными космическими кораблями в варианте «Жизни» — клеточном автомате с правилами B3/S35 (клетка рождается, если у неё три соседа, и выживает, если у неё три или пять соседей).


Связанные конфигурации
Тагалонг (англ. tagalong «тянучка») — конфигурация, которая не является сама по себе космическим кораблём, но может быть присоединена к космическому кораблю, чтобы сформировать новый космический корабль[12]. Другими словами, тагалонг — это часть космического корабля, которую можно удалить без разрушения корабля[13].
Тагалонг, расположенный перед космическим кораблём, называют пушалонгом (англ. pushalong «толкушка»)[14].
Конфигурация, способная изменять направление движения космического корабля, не разрушаясь при этом, называется отражателем (англ. reflector).
Ружьё (англ. gun) — неподвижная конфигурация, периодически выпускающая космический корабль[15].
Значение
Космические корабли могут использоваться для передачи информации. Способность планера переносить информацию стала частью доказательства, что «Жизнь» является тьюринг-полной[16][17].
Примечания
- Клумова И. Н. Игра «Жизнь» // Квант. — 1974. — № 9. — С. 26—30.
- ЛКК (лёгкий космический корабль). Словарь Жизни.
- СКК (средний космический корабль). Словарь Жизни.
- ТКК (тяжёлый космический корабль). Словарь Жизни.
- Не путать с кораблём (ship) — устойчивой конфигурацией.
- Космический корабль. Словарь Жизни.
- Глайдер. Словарь Жизни.
- Spaceship. ConwayLife.com.
- Oblique Life spaceship created. Game of Life News (19 мая 2010). Дата обращения: 10 августа 2013.
- Скорость света. Словарь Жизни.
- Speed. ConwayLife.com.
- Тагалонг. Словарь Жизни.
- Tagalong. Eric Weisstein's Treasure Trove of Life C.A..
- Пушалонг. Словарь Жизни.
- Ружьё. Словарь Жизни.
- Paul Chapman. Life Universal Computer (11 ноября 2002). Дата обращения: 12 июля 2009.
- Berlekamp, E. R.; Conway, John Horton & Guy, R.K. (2004), Winning Ways for your Mathematical Plays (2nd ed.), A K Peters Ltd, ISBN 978-1-56881-130-7; ISBN 1-56881-142-X; ISBN 1-56881-143-8; ISBN 1-56881-144-6
Ссылки
- Николай Белюченко. Словарь Жизни. Архивировано 10 октября 2012 года.
- Stephen A. Silver. Life Lexicon. Архивировано 26 мая 2013 года.
- Николай Белюченко. Космические корабли в Жизни Конуэя. Архивировано 3 октября 2012 года.
- David I. Bell. Spaceships in Conway's Game of Life.
- David Eppstein. Gliders in "Life"-Like Cellular Automata.
- Achim Flammenkamp. Natural Spaceships in Game of Life. — корабли, появляющиеся в случайных конфигурациях.
- Spaceships Archives. Game of Life News.