Задача синхронизации стрелков

Зада́ча синхрониза́ции стрелко́в — задача из области информатики и теории клеточных автоматов.

Впервые предложенная Джоном Майхиллом в 1957 году и опубликованная (с решением) в 1962 году Эдвардом Муром[1].

Формулируется следующим образом:

Рассмотрим конечное, но произвольное число клеточных конечных автоматов (стрелков), выстроенных в ряд. В момент времени

t=0

каждый солдат находится в исходном состоянии, за исключением самого левого солдата (командира). Состояние каждого солдата в момент времени

t>0

зависит от состояния его самого и двух его соседей в момент времени

t-1

(за исключением самых крайних солдат, у которых только один сосед). Если солдат и его соседи находятся в исходном состоянии, то в этом же состоянии они и остаются в следующие моменты времени. Задача заключается в том, чтобы найти конечный набор состояний клеток клеточного автомата и правил перехода между ними, которые допускали бы одновременный переход всех солдат (клеток) в требуемое конечное состояние (огонь).

История

Одно из решений задачи с использованием 15 состояний у каждого стрелка и

3n

единиц времени. Время нарастает сверху вниз.

Решение продолжительностью

2n-2

единиц времени. Время нарастает сверху вниз.

Первое решение этой задачи было найдено Джоном Маккарти и Марвином Мински и было опубликовано в Sequential Machines Эдвардом Муром. Лучшее из известных решений, использующее шесть состояний, было найдено Жаком Мазойером в 1987 году[2]. Ранее Роберт Бальцер доказал, что решений с четырьмя состояниями клеток не существует[3]. Питер Сандерс позднее выяснил, что поисковая процедура Бальцера была неполной, однако исправив процедуру, получил тот же результат. До сих пор неизвестно, существует ли решение с пятью состояниями клеток.

Решение, требующее минимальное время, было найдено профессором Е. Гото из МТИ[4]. Оно использует несколько тысяч состояний и требует ровно $2n-2$ единиц времени для $n$ солдат. Строго доказано, что более эффективных по времени решений не существует.

Общее решение

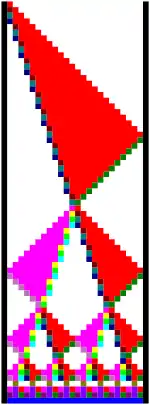
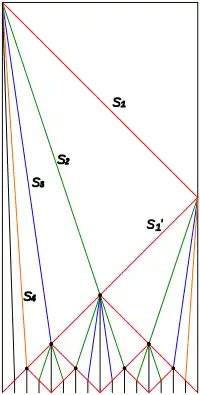
Общее решение задачи описывает две волны состояний, распространяющиеся по ряду солдат, одна из которых движется в три раза быстрее другой. Быстрая волна отражается от дальнего края ряда и встречается с медленной в центре. После этого две волны разделяются на четыре, движущиеся в разные стороны от центра. Процесс продолжается, каждый раз удваивая число волн, пока длина отрезков ряда не станет равной 1. В этот момент все солдаты стреляют. Это решение требует $3n$ единиц времени для $n$ солдат.

Решение, требующее минимального времени

Оптимальное по времени решение впервые было описано в статье Абрахама Ваксона в 1966 году[5]. Командир посылает соседнему солдату сигналы $S_{1},~~S_{2},~~S_{3}~~\dots ~~S_{i}~$ с частотами $1,~{\frac {1}{3}},~{\frac {1}{7}},~\dots ~{\frac {1}{2^{i-1}-1}}.$ Сигнал $S_{1}$ отражается от правого края ряда и встречает сигнал $S_{i}$ (для $i\geq 2$ ) в ячейке $n/2^{i-1}.$ Когда $S_{1}$ отражается, он также создает нового командира на правом конце.

Сигналы $S_{i}$ генерируются с использованием вспомогательных сигналов, распространяющихся влево. Каждый второй момент времени обычный сигнал генерирует вспомогательный сигнал, распространяющийся влево. $S_{1}$ движется самостоятельно со скоростью 1, тогда как более медленные сигналы движутся только при получении вспомогательных сигналов.

Обобщения

Было предложено и изучено несколько более общих формулировок задачи, включая ряды с произвольным расположением командира, замкнутые кольца, квадраты, кубы, графы Кэли и графы общего вида.

Примечания

F. R. Moore, G. G. Langdon, A generalized firing squad problem. Information and Control, Volume 12, Issue 3, March 1968, Pages 212—220. DOI
Jacques Mazoyer, A six-state minimal time solution to the firing squad synchronization problem. Theoretical Computer Science, 1987, vol. 50 pp 183—238 DOI
Robert Balzer, An 8-state Minimal Time Solution to the Firing Squad Synchronization Problem. Information and Control, 1967, vol.10, pp.22—42 DOI
Goto E. A minimal time solution of the firing squad problem. Dittoed course notes for Applied Mathematics, vol.298,pp.52-59. Harvard University, Cambridge(1962)
Abraham Waksman, An Optimum Solution to the Firing Squad Synchronization Problem. Information and Control, 1966, vol.9, pp.66—78 DOI

Литература

Shinahr, Ilka. Two- and three-dimensional firing-squad synchronization problem (англ.) // Information and Control : journal. — Academic Press, 1974. — Vol. 24. — P. 163—180. — doi:10.1016/S0019-9958(74)80055-0.

Ссылки

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] F. R. Moore, G. G. Langdon, A generalized firing squad problem. Information and Control, Volume 12, Issue 3, March 1968, Pages 212—220. DOI

[2] Jacques Mazoyer, A six-state minimal time solution to the firing squad synchronization problem. Theoretical Computer Science, 1987, vol. 50 pp 183—238 DOI

[3] Robert Balzer, An 8-state Minimal Time Solution to the Firing Squad Synchronization Problem. Information and Control, 1967, vol.10, pp.22—42 DOI

[4] Goto E. A minimal time solution of the firing squad problem. Dittoed course notes for Applied Mathematics, vol.298,pp.52-59. Harvard University, Cambridge(1962)

[5] Abraham Waksman, An Optimum Solution to the Firing Squad Synchronization Problem. Information and Control, 1966, vol.9, pp.66—78 DOI