Теорема сумм-произведений

Наиболее удобными для изучения оказываются крайние случаи гипотезы:

• few sums, many product (FSMP): если ${\displaystyle |A+A|\ll |A|}$, то ${\displaystyle |AA|\geq |A|^{2-o(1)}}$[1]

• few products, many sums (FPMS): если ${\displaystyle |AA|\ll |A|}$, то ${\displaystyle |A+A|\geq |A|^{2-o(1)}}$[2]

При ${\displaystyle {\mathbb {F} }={\mathbb {R} }}$ теорема сумм-произведений иногда называется также теоремой Эрдёша-Семереди, поскольку именно они в 1983 году подняли вопрос рассмотрения соотношения количеств сумм и произведений. В той же работе они выдвинули гипотезу о том, что величина ${\displaystyle \varepsilon }$ может быть сколь угодно близка к единице (то есть ${\displaystyle \max \left\lbrace {|A+A|,|A\times A|}\right\rbrace >|A|^{2-o(1)}}$). Однако В той же статье они выдвинули ещё несколько гипотез, в частности, аналогичную для ${\displaystyle k}$ слагаемых и множеств: ${\displaystyle \max \left\lbrace {|A+\dots +A|,|A\times \dots \times A|}\right\rbrace >|A|^{k-o(1)}}$.

Хронология улучшения ${\displaystyle \delta }$ в оценке ${\displaystyle \max\{|A+A|,|AA|\}\geq |A|^{1+\delta -o(1)},\ A\subset {\mathbb {R} }}$
Год	Значение ${\displaystyle \delta }$	Автор(ы)
1983	${\displaystyle 1/31}$(*)(**)	Эрдёш, Семереди[4] ${\displaystyle 1+\delta }$ вместо ${\displaystyle 1+\delta -o(1)}$
1998	${\displaystyle 1/15}$(*)(**)	Форд[5]
1997	${\displaystyle 1/4}$(**)	Элекеш[6]
2005	${\displaystyle 3/11}$	Шоймоши[7]
2009	${\displaystyle 1/3}$	Шоймоши[8]
2015	${\displaystyle {\frac {1}{3}}+{\frac {1}{20598}}\approx 0.333381...}$	Конягин, Шкредов[9]
2016	${\displaystyle {\frac {1}{3}}+{\frac {5}{9813}}\approx 0.333842...}$	Конягин, Шкредов[10]
2016	${\displaystyle {\frac {1}{3}}+{\frac {1}{1509}}\approx 0.333996...}$	Руднев, Шкредов, Стивенс[11]
2019	${\displaystyle {\frac {1}{3}}+{\frac {5}{5277}}\approx 0.334280...}$	Шакан[12]
2020 (препринт)	${\displaystyle {\frac {1}{3}}+{\frac {2}{1167}}\approx 0.335047...}$	Руднев, Стивенс[13]
(*) Только для ${\displaystyle A\subset {\mathbb {Z} }}$ (**) Верно и для степени ${\displaystyle 1+\delta }$ вместо ${\displaystyle 1+\delta -o(1)}$

Теренс Тао в своей монографии отмечает, что задача о получении аналога результата Эрдёша и Семереди в полях ${\displaystyle {\mathbb {F} }_{p}}$ была поставлена в 1999 г. Т. Вольфом (в частной беседе) для подмножеств ${\displaystyle A\subset {\mathbb {F} }_{p}}$ мощности порядка ${\displaystyle p^{1/2}}$.

Задача сумм-произведений в ${\displaystyle {\mathbb {F} }_{p}}$ была решена в работах Бургейн, Глиббичука и Конягина и Бургейна, Каца и Тао. Они доказали следующую теорему

В условии теоремы требование ${\displaystyle |A|<p^{1-\varepsilon }}$ является естественным, так как если ${\displaystyle |A|}$ имеет порядок близкий к ${\displaystyle p}$, то обе величины ${\displaystyle |A+A|}$ и ${\displaystyle |A\times A|}$ будут по порядку близки к ${\displaystyle |A|}$.[14]

Теренс Тао исследовал границы возможностей обобщения теоремы на произвольные кольца и, в частности, связь экстремальных случаев малых значений ${\displaystyle |A+A|}$ и ${\displaystyle |A\cdot A|}$ с количеством делителей нуля в множестве ${\displaystyle A}$ и близостью его структуры к подкольцу.[15]

Доказательство Эрдёша и Семереди использовало тот факт, что при малых ${\displaystyle |A+A|}$ и ${\displaystyle |A\times A|}$ существует решение системы

${\displaystyle {\begin{cases}b_{1}+b_{3}=b_{2}+b_{4}\\b_{1}b_{5}=b_{2}b_{6}\ ,\end{cases}}}$

где ${\displaystyle b_{i}}$ принадлежат некоторым (разным) подмножествам ${\displaystyle A}$, а на само множество ${\displaystyle A}$ налагаются специальные условия. Используя такое утверждение как лемму, можно доказать теорему и для произвольного множества ${\displaystyle A}$.[16]

Если все элементы ${\displaystyle a\in A}$ имеют много представлений в виде ${\displaystyle a=p_{1}p_{2},\ p_{1}\in \Pi _{1},\ p_{2}\in \Pi _{2}}$ для некоторых небольших множеств ${\displaystyle \Pi _{1}\Pi _{2}}$, то для оценки числа решений уравнения

${\displaystyle a+b=c,\ a\in A,\ b\in B,\ c\in C\ .}$

с любыми множествами ${\displaystyle B,C}$ можно использовать уравнение

${\displaystyle p_{1}p_{2}+b=c,\ p_{1}\in \Pi _{1},\ p_{2}\in \Pi _{2},\ b\in B,\ c\in C\ .}$

С другой стороны, решения такого уравнения соответствуют инциденциям между прямыми, которые параметризуются парами ${\displaystyle (p_{1},b)}$, и точками, которые параметризуются парами ${\displaystyle (p_{2},c)}$. Поэтому для их оценки оказывается удобно использовать общие результаты об инциденциях, наилучший из которых — теорема Семереди — Троттера.[17][18]

Именно это использовал Элекеш при доказательстве теоремы с показателем ${\displaystyle \delta ={\frac {1}{4}}}$.[6] Неявно его доказательство можно разделить на два этапа:

• анализ уравнения ${\displaystyle a+b=c,\ a\in A,b\in B,c\in C}$ (тривиально, с помощью разложения ${\displaystyle \Pi _{1}:=AA,\ \Pi _{2}:=1/A}$)

• применение полученных оценок (тривиально, для ${\displaystyle B:=A,\ C:=A+A}$)

Такая декомпозиция важна для осмысления возникших позже методов.

Конструкция Шоймоши. Красные точки имеют координаты из ${\displaystyle A\times A}$.
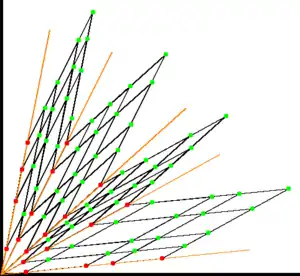
Зелёные точки соответствуют суммам красных с соседних прямых. Все они гарантированно различны и принадлежат ${\displaystyle (A+A)\times (A+A)}$.
Количество линий с красными точками выражается через ${\displaystyle |AA|}$

Шоймоши использовал тот факт, что если ${\displaystyle {\frac {a}{b}}<{\frac {c}{d}}}$, то

${\displaystyle {\frac {a}{b}}<{\frac {a+c}{b+d}}<{\frac {c}{d}}\ .}$

Из этого следует, что если ${\displaystyle {\frac {a_{1}}{b_{1}}}<{\frac {a_{2}}{b_{2}}}<{\frac {a_{3}}{b_{3}}}}$, то

${\displaystyle {\frac {a_{1}+a_{2}}{b_{1}+b_{2}}}<{\frac {a_{2}+a_{3}}{b_{2}+b_{3}}}\ .}$

В то же время при фиксированных значениях ${\displaystyle \lambda \in A/A,\ \mu \in A/A}$ все пары ${\displaystyle (a+c,b+d)}$, образуемые представлениями

${\displaystyle \lambda ={\frac {a}{b}},\ \mu ={\frac {c}{d}},\ a,b,c,d\in A}$

будут различны, поэтому, просуммировав их по «соседним» парам ${\displaystyle (\lambda ,\mu )}$, можно получить оценку на ${\displaystyle |A+A|}$ в терминах числа таких представлений. А оно, в свою очередь, выражается (опосредовано) через ${\displaystyle |AA|}$.[19]

Наиболее наглядно эту идею можно выразить геометрически, как суммирование точек из ${\displaystyle A\times A}$, которые лежат на соседних прямых, исходящих из центра координат.

Разбиение конструкции Шоймоши по методу Конягина-Шкредова
Цвета линий, исходящих из центра координат, соответствуют блокам, в каждом из которых оценивается количество совпадений сумм.
Синие и фиолетовые линии обозначают суммируемые пары красных точек с одинаковыми суммами.

Если в конструкции Шоймоши убрать условие о том, что суммируемые точки должны принадлежать соседним прямым, то уже ничто не будет гарантировать, что все получающиеся суммы будут различны. Например, вообще все суммы точек из ${\displaystyle A\times A}$ могут быть различны только в экстремальном случае ${\displaystyle |A+A|\gg |A|^{2}}$, а он уже удовлетворяет гипотезе сумм-произведений.

Исходя из этого, Конягин и Шкредов оценили минимальное число совпадений таких сумм в промежуточном случае (когда ${\displaystyle |A+A|}$ и ${\displaystyle |AA|}$ равны нижней оценке, то есть ${\displaystyle |A|^{4/3}}$). Чтобы оценить число совпадений, они разбили все прямые на блоки из одинакового числа идущих подряд и оценивали число совпадений в каждом блоке для большинства из них. Используя эти оценки, они получили результат с ${\displaystyle \delta >{\frac {1}{3}}}$.[20]

Совпадения двух сумм точек, которые рассматривали Конягин и Шкредов, означают наличие решения системы уравнений

${\displaystyle {\begin{cases}\lambda _{1}a_{1}+\lambda _{2}a_{2}=\lambda _{3}a_{3}+\lambda _{4}a_{4}\\a_{1}+a_{2}=a_{3}+a_{4}\ ,\end{cases}}}$

где ${\displaystyle (a_{i},\lambda _{i}a_{i})\in A\times A}$ и все ${\displaystyle \lambda _{i}}$ и пары ${\displaystyle (\lambda _{1},\lambda _{2}),(\lambda _{3},\lambda _{4})}$ различны. Редуцируя систему по методу Гаусса (в одно действие), можно получить уравнение

${\displaystyle a_{3}=c_{1}a_{1}-c_{2}a_{2}}$

с постоянными ${\displaystyle c_{1},c_{2}}$ и теми же условиями на ${\displaystyle a_{1},a_{2}}$. Руднев и Стивенс применили это для явного построения мультипликативного разложения большого подмножества ${\displaystyle A}$ с лучшими свойствами, чем у тривиального.[21]

По аналогии с доказательством Элекеша, это позволяет разделить доказательство оценок с показателем ${\displaystyle \delta ={\frac {1}{3}}+c}$ на два этапа:

• применение нового мультипликативного разложения;

• нетривиальное применение уравнения ${\displaystyle a-b=c}$ для оценки ${\displaystyle |A+A|}$.[22]

Наиболее популярный путь использования уравнений для оценки ${\displaystyle |A+A|}$ — использование аддитивной энергии и её обобщений. Результаты применения теоремы Семереди-Троттера позволяют лучше всего анализировать уравнения вида

${\displaystyle E_{3}(A,D):=\{(a_{1},a_{2},a_{3},d_{1},d_{2},d_{3})\in A^{3}\times D^{3}\$ :\ a_{1}-d_{1}=a_{2}-d_{2}=a_{3}-d_{3}\}}

для произвольного ${\displaystyle D}$. Руднев и Стивенс предложили метод использования такой аддитивной энергии с помощью рассмотрения уравнения

${\displaystyle d=(a+b)-(a+c)\,\ a,b,c\in A,\ d\in D\ ,}$

где ${\displaystyle D}$ соответствует множеству популярных (с большим количеством представлений) разностей, а ${\displaystyle a+b}$ принадлежит множеству популярных сумм. Кроме задачи сумм-произведений, разработка подобных методов актуальна для оценки сумм выпуклых последовательностей.[23]

Существует похожий операторный метод, который менее эффективен для оценки ${\displaystyle |A+A|}$, но позволяет лучше изучать связь между ${\displaystyle E(A)}$ и ${\displaystyle |AA|}$.[24]

При доказательстве теоремы для ${\displaystyle {\mathbb {F} }={\mathbb {F} }_{p}}$ широко используются понятие аддитивной энергии, неравенство Плюннеке — Ружа и оценки Балога-Семереди-Гауэрса. Одно из возможных доказательств использует нижнюю оценку на размер множества ${\displaystyle R(A)=A\left({{\frac {A\times A-A\times A}{A-A}}+A}\right)}$ и тот факт, что из верхних оценок на размеры ${\displaystyle A+A}$ и ${\displaystyle A\times A}$ следует противоречащая нижней верхняя оценка на размер ${\displaystyle R(A)}$.[25][26]

Бургейн и Чанг рассматривали оценки вида

${\displaystyle \max\{|\underbrace {A+\dots +A} _{k}|,|\underbrace {A\times \dots \times A} _{k}|\}\geq |A|^{b(k)}}$

для произвольного ${\displaystyle k}$ и ${\displaystyle b(k)\to \infty }$.[30]

Во многих работах сложение и умножение соединяют в одном выражении: например, получают безусловные нижние оценки для ${\displaystyle |AA+AA|}$.[31]

Одно из обобщений гипотезы — вопрос о суммах и произведениях, соответствующие рёбрам произвольного графа на элементах множества.

В отличие от случая ${\displaystyle G=A\times A}$, здесь может не наблюдаться экстремального роста ни сумм, ни произведений: при ${\displaystyle c<1}$ возможна ситуация, когда ${\displaystyle \delta <c}$[32]. Поэтому кроме нижних оказывается актуален вопрос верхних оценок на ${\displaystyle \max\{|A+A|,|AA|\}}$. Впрочем, нижние оценки тоже исследуются.[33][34]

Нижние оценки на размер множества сумм легко выводить из верхних оценок на аддитивную энергию, поэтому гипотезу о первых естественно обобщить до гипотезы о вторых, используя аналогичное понятие мультипликативной энергии.

Но у множества чисел вполне могут быть большими одновременно обе энергии, поскольку нижняя оценка может контролироваться вкладом отдельного подмножества. Например, если ${\displaystyle E^{+}(A_{1})\gg |A|^{3},E^{\times }(A_{2})\gg |A|^{3}}$, то для множества ${\displaystyle A=A_{1}\cup A_{2}}$ верно, что

${\displaystyle \min\{E^{+}(A),E^{\times }(A)\}\geq \min\{E^{+}(A_{1}),E^{\times }(A_{2})\}\gg |A|^{3}\ .}$

Поэтому при формулировке соответствующей теоремы об энергиях используется соотношение энергий разных подмножеств.

Наилучший вариант этой теоремы доказан для ${\displaystyle \delta ={\frac {7}{26}}-o(1)}$.[12] Известно, что аналогичное не верно для ${\displaystyle \delta >{\frac {2}{3}}}$.[35]

Умножение двух чисел можно представить как функцию от сложения их логарифмов: ${\displaystyle ab=\exp(\log a+\log b)}$. Поэлементное применение строго возрастающей функции ко множеству не меняет его размера, поэтому

${\displaystyle |AA|=|\exp(\log A+\log A)|=|\log A+\log A|}$

и основную гипотезу сумм-произведений можно переформулировать как

${\displaystyle \max\{|A+A|,|\log A+\log A|\}\geq |A|^{2-o(1)}}$

или (подставляя ${\displaystyle A:=\log A}$) как

${\displaystyle \max\{|\exp(A)+\exp(A)|,|A+A|\}\geq |A|^{2-o(1)}\ .}$

Оказывается, что похожие оценки можно доказать для произвольной выпуклой функции вместо ${\displaystyle \exp }$.

Вопрос о том, верны ли такие же оценки с показателем ${\displaystyle 2-o(1)}$ в правой части, остаётся открытым.

Аналогичные результаты получены и для большего числа слагаемых.[37]