Метод Гаусса

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы[1].

История

Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах».[2]

Описание метода

Пусть исходная система выглядит следующим образом:

\left\{{\begin{array}{lcr}a_{11}x_{1}+\ldots +a_{1n}x_{n}&=&b_{1}\\\ldots &&\\a_{m1}x_{1}+\ldots +a_{mn}x_{n}&=&b_{m}\\\end{array}}\right.

Её можно записать в матричном виде:

Ax=b,

где

A=\left({\begin{array}{ccc}a_{11}&\ldots &a_{1n}\\\ldots &&\\a_{m1}&\ldots &a_{mn}\end{array}}\right),\quad x=\left({\begin{array}{c}x_{1}\\\vdots \\x_{n}\end{array}}\right),\quad b=\left({\begin{array}{c}b_{1}\\\vdots \\b_{m}\end{array}}\right).\quad (1)

Матрица $A$ называется основной матрицей системы, $b$ — столбцом свободных членов.

Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):

\left\{{\begin{array}{rcl}\alpha _{1j_{1}}x_{j_{1}}+\alpha _{1j_{2}}x_{j_{2}}+\ldots +\alpha _{1j_{r}}x_{j_{r}}+\ldots +\alpha _{1j_{n}}x_{j_{n}}&=&\beta _{1}\\\alpha _{2j_{2}}x_{j_{2}}+\ldots +\alpha _{2j_{r}}x_{j_{r}}+\ldots +\alpha _{2j_{n}}x_{j_{n}}&=&\beta _{2}\\&\ldots &\\\alpha _{rj_{r}}x_{j_{r}}+\ldots +\alpha _{rj_{n}}x_{j_{n}}&=&\beta _{r}\\0&=&\beta _{r+1}\\&\ldots &\\0&=&\beta _{m}\end{array}}\right.,

где $\alpha _{1j_{1}},\ldots ,\alpha _{rj_{r}}\neq 0.$

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных $x_{j_{1}},\ldots ,x_{j_{r}}$ [3].

Тогда переменные $x_{j_{1}},\ldots ,x_{j_{r}}$ называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число $\beta _{i}\neq 0$ , где $i>r$ , то рассматриваемая система несовместна, т. е. у неё нет ни одного решения.

Пусть $\beta _{i}=0$ для любых $i>r$ .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом $x$ ( $\alpha _{ij_{i}},\,i=1,\ldots ,r$ , где $i$ — номер строки):

\left\{{\begin{array}{rcc}x_{j_{1}}+{\widehat {\alpha }}_{1j_{2}}x_{j_{2}}+\ldots +{\widehat {\alpha }}_{1j_{r}}x_{j_{r}}&=&{\widehat {\beta }}_{1}-{\widehat {\alpha }}_{1j_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{1j_{n}}x_{j_{n}}\\x_{j_{2}}+\ldots +{\widehat {\alpha }}_{2j_{r}}x_{j_{r}}&=&{\widehat {\beta }}_{2}-{\widehat {\alpha }}_{2j_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{2j_{n}}x_{j_{n}}\\&\ldots &\\x_{j_{r}}&=&{\widehat {\beta }}_{r}-{\widehat {\alpha }}_{rj_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{rj_{n}}x_{j_{n}}\\\end{array}}\right.,\qquad {\widehat {\beta }}_{i}={\frac {\beta _{i}}{\alpha _{ij_{i}}}},\quad {\widehat {\alpha }}_{ij_{k}}={\frac {\alpha _{ij_{k}}}{\alpha _{ij_{i}}}}\quad (2)

,

где $i=1,\ldots ,r,\quad k=i+1,\ldots ,n.$

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Следствия:
1: Если в совместной системе все переменные главные, то такая система является определённой.

2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.

Критерий совместности

Упомянутое выше условие $\beta _{i}=0$ для всех $i>r$ может быть сформулировано в качестве необходимого и достаточного условия совместности:

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

Теорема Кронекера — Капелли.
Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.

Следствия:

Количество главных переменных равно рангу системы и не зависит от её решения.
Если ранг совместной системы равен числу переменных данной системы, то она определена.

Алгоритм

Блок-схема представлена на рисунке. Данный рисунок — адаптированный для написания программы на языке С/С++, где a — расширенная матрица, последний столбец в которой — столбец свободных членов. Количество строк — n.

Алгоритм Гаусса для решения СЛАУ

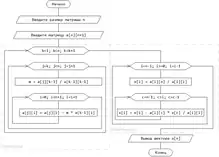
Описание

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. Для этого среди элементов первого столбца матрицы выбирают ненулевой, перемещают содержащую его строку в крайнее верхнее положение, делая эту строку первой. Далее ненулевые элементы первого столбца всех нижележащих строк обнуляются путём вычитания из каждой строки первой строки, домноженной на отношение первого элемента этих строк к первому элементу первой строки. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают, пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует $O(n^{3})$ арифметических операций.

Этот метод опирается на:

Теорема (о приведении матриц к ступенчатому виду).
Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.

Простейший случай

В простейшем случае алгоритм выглядит так:

\left\{{\begin{array}{lcc}a_{11}\cdot x_{1}+a_{12}\cdot x_{2}+\ldots +a_{1n}\cdot x_{n}&=b_{1}&(1)\\a_{21}\cdot x_{1}+a_{22}\cdot x_{2}+\ldots +a_{2n}\cdot x_{n}&=b_{2}&(2)\\\ldots &&\\a_{m1}\cdot x_{1}+a_{m2}\cdot x_{2}+\ldots +a_{mn}\cdot x_{n}&=b_{m}&(m)\end{array}}\right.

Прямой ход:

{\begin{array}{ccc}(2)\to (2)-(1)\cdot ({\frac {a_{21}}{a_{11}}})&:&a_{22}^{\prime }\cdot x_{2}+a_{23}^{\prime }\cdot x_{3}+\ldots +a_{2n}^{\prime }\cdot x_{n}=b_{2}^{\prime }\\(3)\to (3)-(1)\cdot ({\frac {a_{31}}{a_{11}}})&:&a_{32}^{\prime }\cdot x_{2}+a_{33}^{\prime }\cdot x_{3}+\ldots +a_{3n}^{\prime }\cdot x_{n}=b_{3}^{\prime }\\\ldots &&\\(m)\to (m)-(1)\cdot ({\frac {a_{m1}}{a_{11}}})&:&a_{m2}^{\prime }\cdot x_{2}+a_{m3}^{\prime }\cdot x_{3}+\ldots +a_{mn}^{\prime }\cdot x_{n}=b_{n}^{\prime }\\(3)\to (3)-(2)\cdot ({\frac {a_{32}^{\prime }}{a_{22}^{\prime }}})&:&a_{33}^{\prime \prime }\cdot x_{3}+\ldots +a_{3n}^{\prime \prime }\cdot x_{n}=b_{3}^{\prime \prime }\\\ldots &&\\(m)\to (m)-(m-1)\cdot ({\frac {a_{m,n-1}^{(m-2)}}{a_{m-1,n-1}^{(m-2)}}})&:&a_{mm}^{(m-1)}\cdot x_{m}+\ldots +a_{mn}^{(m-1)}\cdot x_{n}=b_{m}^{(m-1)}\end{array}}

Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

Пример

Покажем, как методом Гаусса можно решить следующую систему:

\left\{{\begin{array}{ccc}2x+y-z&=&8\\-3x-y+2z&=&-11\\-2x+y+2z&=&-3\end{array}}\right.

Обнулим коэффициенты при $x$ во второй и третьей строчках. Для этого прибавим к ним первую строчку, умноженную на $\textstyle {\frac {3}{2}}$ и $1$ , соответственно:

\left\{{\begin{array}{rcc}2x+y-z&=&8\\{\frac {1}{2}}y+{\frac {1}{2}}z&=&1\\2y+z&=&5\end{array}}\right.

Теперь обнулим коэффициент при $y$ в третьей строке, вычтя из неё вторую строку, умноженную на $4$ :

\left\{{\begin{array}{rcc}2x+y-z&=&8\\{\frac {1}{2}}y+{\frac {1}{2}}z&=&1\\-z&=&1\\\end{array}}\right.

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

z=-1

из третьего;

y=3

из второго, подставив полученное

z

x=2

из первого, подставив полученные

z

и

y

.

Таким образом, исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

Реализация алгоритма на языке программирования C#

namespace Gauss_Method
{
    class Maths
    {
        /// <summary>
        /// Метод Гаусса (Решение СЛАУ)
        /// </summary>
        /// <param name="Matrix">Начальная матрица</param>
        /// <returns></returns>
        public static double[] Gauss(double[,] Matrix)
        {
            int n = Matrix.GetLength(0); //Размерность начальной матрицы (строки)
            double[,] Matrix_Clone = new double[n, n + 1]; //Матрица-дублер
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n + 1; j++)
                    Matrix_Clone[i, j] = Matrix[i, j];

            //Прямой ход (Зануление нижнего левого угла)
            for (int k = 0; k < n; k++) //k-номер строки
            {
                for (int i = 0; i < n + 1; i++) //i-номер столбца
                    Matrix_Clone[k, i] = Matrix_Clone[k, i] / Matrix[k, k]; //Деление k-строки на первый член !=0 для преобразования его в единицу
                for (int i = k + 1; i < n; i++) //i-номер следующей строки после k
                {
                    double K = Matrix_Clone[i, k] / Matrix_Clone[k, k]; //Коэффициент
                    for (int j = 0; j < n + 1; j++) //j-номер столбца следующей строки после k
                        Matrix_Clone[i, j] = Matrix_Clone[i, j] - Matrix_Clone[k, j] * K; //Зануление элементов матрицы ниже первого члена, преобразованного в единицу
                }
                for (int i = 0; i < n; i++) //Обновление, внесение изменений в начальную матрицу
                    for (int j = 0; j < n + 1; j++)
                        Matrix[i, j] = Matrix_Clone[i, j];
            }

            //Обратный ход (Зануление верхнего правого угла)
            for (int k = n - 1; k > -1; k--) //k-номер строки
            {
                for (int i = n; i > -1; i--) //i-номер столбца
                    Matrix_Clone[k, i] = Matrix_Clone[k, i] / Matrix[k, k];
                for (int i = k - 1; i > -1; i--) //i-номер следующей строки после k
                {
                    double K = Matrix_Clone[i, k] / Matrix_Clone[k, k];
                    for (int j = n; j > -1; j--) //j-номер столбца следующей строки после k
                        Matrix_Clone[i, j] = Matrix_Clone[i, j] - Matrix_Clone[k, j] * K;
                }
            }

            //Отделяем от общей матрицы ответы
            double[] Answer = new double[n];
            for (int i = 0; i < n; i++)
                Answer[i] = Matrix_Clone[i, n];

            return Answer;
        }
    }
}

Применение и модификации

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:

нахождения матрицы, обратной к данной (к матрице справа приписывается единичная такого же размера, что и исходная: $[A|E]$ , после чего $A$ приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица: $[E|A^{-1}]$ );
определения ранга матрицы (согласно следствию из теоремы Кронекера — Капелли ранг матрицы равен числу её главных переменных);
численного решения СЛАУ в технических приложениях (для уменьшения погрешности вычислений используется Метод Гаусса с выделением главного элемента, суть которого заключена в том, чтобы на каждом шаге в качестве главной переменной выбирать ту, при которой среди оставшихся после вычёркивания очередных строк и столбцов стоит максимальный по модулю коэффициент).

Достоинства метода

Для матриц ограниченного размера — менее трудоёмкий по сравнению с другими методами.
Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.
Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы[4].

Устойчивость метода Гаусса

Метод Гаусса для плохо обусловленных матриц коэффициентов является вычислительно неустойчивым. Например, для матриц Гильберта метод приводит к очень большим ошибкам даже при небольшой размерности этих матриц. Уменьшить вычислительную ошибку можно с помощью метода Гаусса с выделением главного элемента, который является условно устойчивым[5]. Широкое применение метода Гаусса связано с тем, что плохо обусловленные матрицы встречаются на практике относительно редко.

Неоптимальность метода Гаусса

В 1969 году Штрассен доказал, что большие матрицы можно перемножить за время $O(n^{\log _{2}{7}})=O(n^{2{,}81})$ [6]. Отсюда вытекает, что обращение матриц и решение СЛАУ можно осуществлять алгоритмами асимптотически более быстрыми по порядку, чем метод Гаусса. Таким образом, для больших СЛАУ метод Гаусса не оптимален по скорости.

См. также

Примечания

Н. Ш. Кремер, 2.3. «Метод Гаусса», стр. 44
Grcar Joseph F. How ordinary elimination became Gaussian elimination // Historia Mathematica. — Т. 38, вып. 2. — С. 163—218. — doi:10.1016/j.hm.2010.06.003. — arXiv:0907.2397.
Такого расположения минора можно добиться перестановкой столбцов основной матрицы и соответствующей перенумерацией переменных.
Н. Ш. Кремер, 2.4. «Система m линейных уравнений с n переменными», стр. 49
УСТОЙЧИВОСТЬ И ТОЧНОСТЬ ПРЯМЫХ МЕТОДОВ (недоступная ссылка)
Strassen V. Gaussian Elimination is not Optimal (англ.) // Numer. Math / F. Brezzi — Springer Science+Business Media, 1969. — Vol. 13, Iss. 4. — P. 354—356. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF02165411

Литература

И. М. Виноградов. Гаусса метод // Математическая энциклопедия. — М.: Советская энциклопедия (рус.). — 1977—1985.
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.|место = М. |издательство = Лаборатория Базовых Знаний |год = 2000 |страницы = |isbn =}}
Волков Е. А. Численные методы. — М.: Физматлит, 2003.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575—576.
Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов / Под ред. Н. Ш. Кремера. — 3-е изд. — М.: ЮНИТИ-ДАНА, 2007. — 479 с. — ISBN 5-238-00991-7.

Ссылки

Press, WH; Teukolsky, SA; Vetterling, WT & Flannery, BP (2007), Section 2.2, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Н. Ш. Кремер, 2.3. «Метод Гаусса», стр. 44

[2] Grcar Joseph F. How ordinary elimination became Gaussian elimination // Historia Mathematica. — Т. 38, вып. 2. — С. 163—218. — doi:10.1016/j.hm.2010.06.003. — arXiv:0907.2397.

[3] Такого расположения минора можно добиться перестановкой столбцов основной матрицы и соответствующей перенумерацией переменных.

[4] Н. Ш. Кремер, 2.4. «Система m линейных уравнений с n переменными», стр. 49

[5] УСТОЙЧИВОСТЬ И ТОЧНОСТЬ ПРЯМЫХ МЕТОДОВ (недоступная ссылка)

[_f3df977047c196e4-6] Strassen V. Gaussian Elimination is not Optimal (англ.) // Numer. Math / F. Brezzi — Springer Science+Business Media, 1969. — Vol. 13, Iss. 4. — P. 354—356. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF02165411

Словари и энциклопедии	Большая датская
В библиографических каталогах	GND: 4156110-7

Методы решения СЛАУ
Прямые методы	Матричный метод Метод Гаусса Метод Гаусса — Жордана Метод Крамера LU-разложение Разложение Холецкого Метод прогонки
Итерационные методы	Метод Якоби Метод Гаусса — Зейделя Метод итерации Метод релаксации Метод сопряженных градиентов Метод бисопряжённых градиентов Стабилизированный метод бисопряжённых градиентов
Общее	Обратная матрица Проекционные методы решения СЛАУ Предобуславливание