Теорема Лежандра (сферическая тригонометрия)

Сферический треугольник.

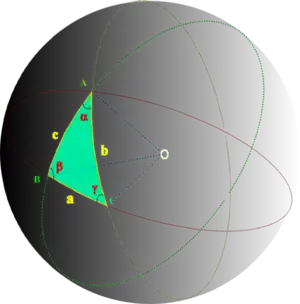
Пусть дан сферический треугольник со сторонами ${\displaystyle a,b,c}$, малыми по сравнению с радиусом сферы ${\displaystyle R}$, углами ${\displaystyle \alpha ,\beta ,\gamma }$ и эксцессом ${\displaystyle \varepsilon =\alpha +\beta +\gamma -\pi }$. Построим на плоскости треугольник со сторонами ${\displaystyle a',b',c'}$, равными по длине соответствующим сторонам данного сферического треугольника, то есть, поскольку для сторон сферического треугольника принята угловая мера, и они выражаются в радианах, то ${\displaystyle a'=aR,b'=bR,c'=cR}$. Обозначим углы такого треугольника (выраженные в радианах) через ${\displaystyle \alpha ',\beta ',\gamma '}$. Теорема Лежандра утверждает, что справедливы соотношения[1]:

${\displaystyle \alpha '\approx \alpha -{\frac {\varepsilon }{3}}}$

${\displaystyle \beta '\approx \beta -{\frac {\varepsilon }{3}}}$

${\displaystyle \gamma '\approx \gamma -{\frac {\varepsilon }{3}}}$

Таким образом, если стороны сферического треугольника малы по сравнению с радиусом сферы, мы можем заменить его на плоский треугольник с такими же по длине сторонами и на треть эксцесса меньшими углами и вычислять элементы плоского треугольника.

Эта теорема была сформулирована А.М.Лежандром в 1787 году[2] и доказана им в 1798 году[3]. Однако, по некоторым источникам, она была известна ещё в 1740 году, когда Ш.М. де ла Кондамин использовал её при обработке градусных измерений перуанской экспедиции[4].