Пятьдесят девять икосаэдров

Пятьдесят девять икосаэдров (англ. The Fifty-Nine Icosahedra) — это книга, написанная и проиллюстрированная Гарольдом Коксетером, Патриком дю Валем, Х. Т. Флазером и Дж. Ф. Петри. В книге перечислены некоторые звёздные формы правильных выпуклых (платоновых) икосаэдров, построенных согласно набору правил, предложенных Дж. Ч. П. Миллером.

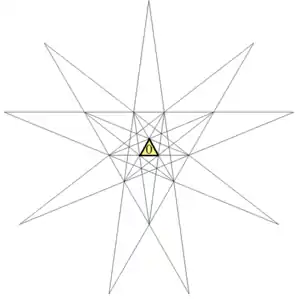
Диаграмма звезды для икосаэдра с центральным треугольником, помеченным для исходного икосаэдра

Книга опубликована издательством университета Торонто в 1938 году. Второе издание выпустило издательство Springer-Verlag в 1982 году. Кейт и Дэвид Креннелы (Crennell) полностью переписали текст и перерисовали вкладки и диаграммы для третьего издания (издательство Tarquin) в 1999 году и добавили новый ссылочный материал и фотографии.

Вклады авторов

Правила Миллера

Хотя Дж. Ч. П. Миллер не занимался непосредственно написанием книги, он был близким коллегой Коксетера и Петри. Его вклад увековечен в его наборе правил для определения, какие звёздчатые формы могут считаться «существенными и различными»:

  1. Грани должны лежать на двадцати плоскостях, то есть, на ограничивающих плоскостях правильного икосаэдра.
  2. Все части, составляющие грани, должны быть теми же самыми в каждой плоскости, даже если они полностью разъединены.
  3. Части, принадлежащие любой (одной) плоскости должны иметь тригональную симметрию с отражением или без. Это обеспечивает икосаэдральную симметрию для всего тела.
  4. Части, принадлежащие любой плоскости должны быть все «доступны» в результирующем теле (то есть они должны быть «внешними». В некоторых случаях мы должны построить модели огромных размеров, чтобы увидеть все части. Для моделей обычного размера некоторые части, хоть они и «внешние», их могут обнаружить только ползающие насекомые).
  5. Исключаются из рассмотрения случаи, когда части можно разделить на два множества, которые по отдельности дают тело с большей симметрией, чем сама фигура. Но мы позволяем соединение энантиоморфной пары, не имеющей общих частей (фактически, это происходит только в одном случае).

Первые три правила соответствуют требованиям симметрии для плоскостей граней. Правило 4 исключает внутренние полости, обеспечивая, чтобы никакие две звёздчатые формы не выглядели идентично. Правило 5 исключает любые несвязные компоненты более простых форм.

Коксетер

Коксетер был основной движущей силой работы. Он провёл анализ, основываясь на правилах Миллера, привлекая ряд техник, таких как комбинаторика и абстрактная теория графов, применение которых в геометрии в те времена было в новинку.

Он заметил, что диаграмма звезды содержит много отрезков. Затем он разработал процедуру работы с комбинациями смежных плоских областей для формального перечисления комбинаций, попадающих под правила Миллера.

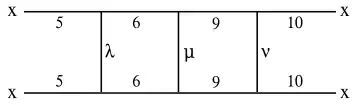
Граф, представленный здесь, показывает связность различных граней, представленных в диаграмме звезды (смотрите ниже). Греческие буквы определяют набор возможных вариантов:

λ может быть 3 или 4
μ может быть 7 или 8
ν может быть 11 или 12

Дю Валь

Дю Валь продумал символические обозначения для наборов конгруэтных ячеек, основываясь на наблюдении, что они лежат на «оболочке» вокруг исходного икосаэдра. Основываясь на этом, он проверил все возможные комбинации на правила Миллера, подтверждая результаты более аналитического подхода Коксетера.

Флазер

Вклад Флазера не был прямым — он сделал картонные модели всех 59 многогранников. До встречи с Коксетером он уже сделал много звёздчатых форм, включая некоторые многогранники, не попадающие под правила Миллера. Он продолжил работу по созданию полной серии, которая хранится в математической библиотеке Кембриджского университера (Англия). В библиотеке хранятся также несколько немиллеровских моделей, но неизвестно, были ли они сделаны позже студентами Флазера или Миллера[1].

Петри

Джон Флиндерс Петри — давний друг Коксетера, имел замечательную способность представлять фигуры в четырёхмерном пространстве. Он и Коксетер работали вместе над многими математическими проблемами. Его прямой вклад в книгу заключается во множестве совершенных трёхмерных рисунков, которые обеспечили очарование книги.

Креннелы

Для третьего издания Кейт и Дэвид Креннелы полностью переработали текст и перерисовали иллюстрации и вкладки. Они также добавили ссылочную секцию, содержащую таблицы, диаграммы и фотографии некоторых моделей из Кембриджа (считавшиеся в то время все сделанными Флазером). Индекс включал все 59 многогранников, пронумерованных последовательно в порядке появления в книге. Несколько ошибок вкралось в процессе редактирования. PDF Файл с исправленными страницами доступен онлайн.

Список пятидесяти девяти икосаэдров
Диаграмма звезды с нумерацией ячеек
Диаграмма ячеек с обозначениями Дю Валя

До Коксетера только Брюкнер и Вилер описали некоторые существенные наборы звёздчатых форм, хотя некоторые, такие как большой икосаэдр, известны и ранее. После публикации книги о 59 икосаэдрах Веннинджер опубликовал инструкции по сборке некоторых моделей из этой серии. Схема нумерации, принятая в его книге, стала широко использоваться, хотя он привёл лишь несколько звёздных форм.

Замечания

Нумерация принадлежит Креннелам, если не указано другое.

Креннелы

  • В нумерации, которую добавили в третье издание Креннелы, первые 32 модели (номера 1-32) зеркально симметричны, а последние 27 (номера 33-59) являются хиральными, и только правая форма приведена в книге. Нумерация соответствует порядку, в котором многогранники появляются в книге.

VRML

  • Ссылка на графические файлы в формате VRML 3D, сделанные Хартом.

Ячейки

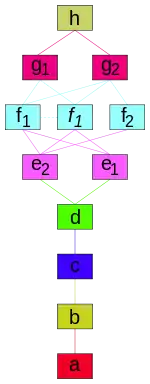
  • Если соединить любую точку пространства отрезком с центром икосаэдра и посчитать число пересечений отрезка с плоскостями граней икосаэдра, получится уровень точки (не считая плоскость, на которой может оказаться сама точка). Все точки с уровнем, не превосходящим некоторое значение, образуют некоторый многогранник. Для правильного икосаэдра возможны 8 таких многогранников, которые обозначаются заглавными буквами A, B, C, …, H, где A — исходный икосаэдр (уровень 0). Существуют точки с уровнями 8 и выше, но соответствующие лучи уходят в бесконечность и такие точки не рассматриваются.
  • Точки одного уровня образуют оболочку. В записи Дю Валя оболочки нумеруются теми же буквами что и многогранники, но прописными. Оболочки состоят из ячеек.
  • Некоторые ячейки разделяются на два типа, им даются индексы. Например, в группу e входят ячейки e1 и e2. Множество f1 подразделяется далее на правую и левую формы, которые обозначаются f1 (обычная буква) и f1 (наклонная). Там, где все уровни представлены, они заменяются большой буквой, заменяя всю последовательность, например, a + b + c + e1 записывается как Ce1.

Грани

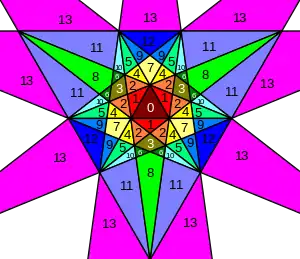
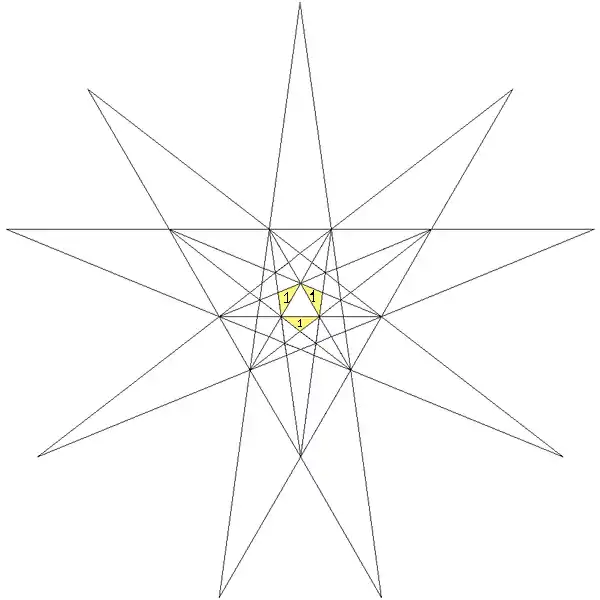
  • Все звёздчатые формы можно определить диаграммой звезды. На приведённой диаграмме окрашенные пронумерованные области показывают части, которые должны появляться вместе как единое целое, если добиваться полной икосаэдральной симметрии. Диаграмма содержит 13 таких наборов. Некоторые из них подразделяются на хиральные пары (не показано), что даёт звёздчатые формы с вращательной симметрией, но не зеркальной. В таблице грани, которые видны снизу, указаны апострофом, например, 3'.

Веннинджер

  • Номера и нумерованные названия соответствуют порядку появления в книге М. Веннинджера Модели многогранников. Порядок, в общем-то, случаен (произвольно выбран редакторами книги) и не несёт никакого математического смысла. Только несколько моделей в книге Веннинджера являются икосаэдрами. Их имена даны в укороченном виде, слова «… икосаэдра» опущены (так, вместо «Вторая звёздчатая форма икосаэдра» в таблице стоит «Вторая звёздчатая форма»).

Вилер

  • Вилер нашёл свои фигуры путём выбора отрезков из диаграммы звезды. Он тщательно дистанцировал этот процесс от классического приведения к звёздчатой форме Кеплера. Коксетер с соавторами игнорировал эти различия.

Брюкнер

  • Брюкнер сделал и сфотографировал модели многих многогранников, только некоторые из которых были икосаэдрами.

Примечания

Таблица пятидесяти девяти икосаэдров
CrennellVRMLCellsГраниВеннинджерВилерБрюкнер Примечания Грань 3D
1 A004
Икосаэдр		1 Платоново тело икосаэдр
2 B126
Первая звёздчатая форма		 2Табл. VIII, рис. 2 Первая звёздчатая форма икосаэдра,
малый триамбический икосаэдр,
или Триакисикосаэдр
3 C223
Соединение пяти октаэдров		3Табл. IX, рис. 6 Правильное соединение пяти октаэдров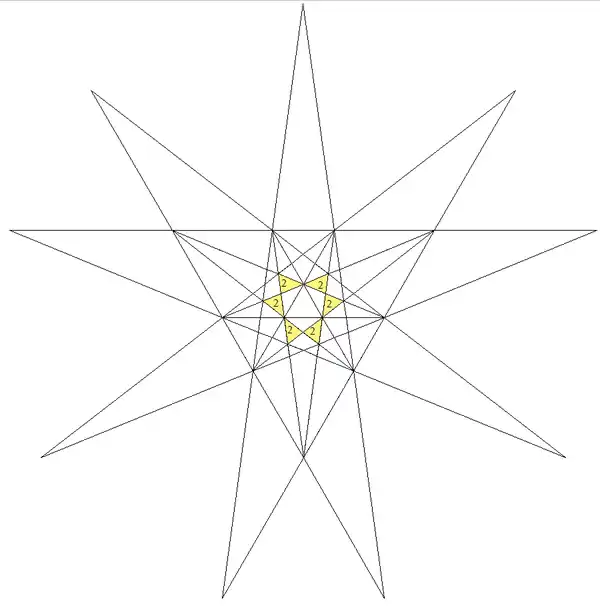
4 D3 4994Табл. IX, рис.17
5 E5 6 79999
6 F8 9 1027

Вторая звёздчатая форма

 19
7 G11 1241
Большой икосаэдр		11Табл. XI, рис. 24 Большой икосаэдр
8 H1342
Завершающая звёздчатая форма		12Табл. XI, рис. 14 Ехиднаэдр
9 e13' 537
Двенадцатая звёздчатая форма		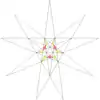99
10 f15' 6' 9 109999
11 g110' 1229
Четвёртая звёздчатая форма		21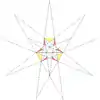
12 e1f13' 6' 9 109999
13 e1f1g13' 6' 9 129920
14 f1g15' 6' 9 129999
15 e24' 6 79999
16 f27' 89922
17 g28' 9' 119999
18 e2f24' 6 89999
19 e2f2g24' 6 9' 119999
20 f2g27' 9' 1130
Пятая звёздчатая форма		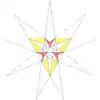99
21 De14 532
Седьмая звёздчатая форма		10
22 Ef17 9 1025
Соединение десяти тетраэдров		8Табл. IX, рис. 3 Правильноесоединение десяти тетраэдров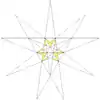
23 Fg18 9 1231
Шестая звёздчатая форма		17Табл. X, рис. 3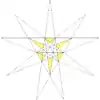
24 De1f14 6' 9 109999
25 De1f1g14 6' 9 129999
26 Ef1g17 9 1228
Третья звёздчатая форма		9Табл. VIII, рис. 26 Выемчатый додекаэдр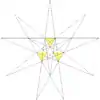
27 De23 6 7995
28 Ef25 6 89918Табл. IX, рис. 20
29 Fg210 1133
Восьмая звёздчатая форма		14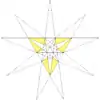
30 De2f23 6 834
Девятая звёздчатая форма		13 Средний триамбикикосаэдр или
Большой триамбикикосаэдр
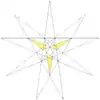31 De2f2g23 6 9' 119999
32 Ef2g25 6 9' 119999
33 f15' 6' 9 1035
Десятая звёздчатая форма		99
34 e1f13' 5 6' 9 1036
Одиннадцатая звёздчатая форма		99
35 De1f14 5 6' 9 109999
36 f1g15' 6' 9 10' 129999
37 e1f1g13' 5 6' 9 10' 1239
Четырнадцатая звёздчатая форма		99
38 De1f1g14 5 6' 9' 10' 129999
39 f1g25' 6' 8' 9' 10 119999
40 e1f1g23' 5 6' 8' 9' 10 119999
41 De1f1g24 5 6' 8' 9' 10 119999
42 f1f2g25' 6' 7' 9' 10 119999
43 e1f1f2g23' 5 6' 7' 9' 10 119999
44 De1f1f2g24 5 6' 7' 9' 10 119999
45 e2f14' 5' 6 7 9 1040
Пятнадцатая звёздчатая форма		99
46 De2f13 5' 6 7 9 109999
47 Ef1 5 6 7 9 10 24
Соединение пяти тетраэдров		 7
(6: левый)		 Табл. IX, рис. 11 Правильное соединение пяти тетраэдров (правый)
48 e2f1g1 4' 5' 6 7 9 10' 12 9999
49 De2f1g1 3 5' 6 7 9 10' 12 9999
50 Ef1g1 5 6 7 9 10' 12 9999
51 e2f1f2 4' 5' 6 8 9 10 38
Тринадцатая звёздчатая форма		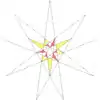99
52 De2f1f2 3 5' 6 8 9 10 9999
53 Ef1f2 5 6 8 9 10 9915
(16: левый)
54 e2f1f2g1 4' 5' 6 8 9 10' 12 9999
55 De2f1f2g1 3 5' 6 8 9 10' 12 9999
56 Ef1f2g1 5 6 8 9 10' 12 9999
57 e2f1f2g2 4' 5' 6 9' 10 11 9999
58 De2f1f2g2 3 5' 6 9' 10 11 9999
59 Ef1f2g2 5 6 9' 10 11 9999

См. также

Примечания
  1. True lost stellations

Литература
  • Max Brückner. Vielecke und Vielflache: Theorie und Geschichte. — Leipzig: B.G. Treubner, 1900. — ISBN 978-1-4181-6590-1.  (нем.) Издание на английском: Polygons and Polyhedra: Theory and History.
  • H. S. M. Coxeter, Patrick du Val, H. T. Flather, J. F. Petrie. The Fifty-nine Icosahedra. — University of Toronto studies, 1938. — (mathematical series 6: 1—26.). Third edition (1999) Tarquin ISBN 978-1-899618-32-3. (англ.)
  • Magnus J. Wenninger. Polyhedron models. — Paperback edition (2003). — Cambridge University Press, 1983. — ISBN 978-0-521-09859-5. (англ.)
  • М. Веннинджер. Модели многогранников. — «Мир», 1974.
  • A. H. Wheeler. Certain forms of the icosahedron and a method for deriving and designating higher polyhedra. — Proceedings of the International Congress of Mathematicians. — Toronto, 1924. — Т. 1. — С. 701—708. (англ.)

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.