Псевдолес

Мы определяем неориентированный граф как множество вершин и рёбер, таких, что каждое ребро содержит две вершины (возможно, совпадающие) в качестве конечных точек. То есть разрешаются кратные рёбра (рёбра с теми же конечными вершинами) и петли (рёбра, конечные вершины которых совпадают) [1]. Подграф графа — это граф, образованный подмножеством вершин и рёбер, такой, что любое ребро в этом подмножестве имеет конечные вершины в подмножестве вершин. Связная компонента неориентированного графа — это подграф, состоящий из вершин и рёбер, которые можно достичь, следуя по рёбрам, исходя из одной стартовой вершины. Граф связан, если любую вершину или ребро можно достичь, следуя из любой другой вершины или ребра. Цикл в неориентированном графе — это связный подграф, в котором любая вершина инцидентна в точности двум рёбрам или является петлёй.

21 граф с одним циклом и максимум шестью вершинами

Псевдолес — это неориентированный граф, в котором каждая связная компонента содержит максимум один цикл [5]. Эквивалентно, это неориентированный граф, в котором у каждой связной компоненты рёбер не больше, чем вершин [6]. Компоненты, не имеющие циклов — это просто деревья, а компоненты, имеющие единственный цикл, называются 1-деревьями или одноцикловыми графами. То есть 1-дерево — это связный граф, содержащий в точности один цикл. Псевдолес с единственной связной компонентой (обычно называемый псевдодеревом, хотя некоторые авторы определяют псевдодерево как 1-дерево) является либо деревом, либо 1-деревом. В общем случае псевдолес может содержать несколько связных компонент, все из которых являются деревьями или 1-деревьями.

Если удалить из 1-дерева одно из рёбер цикла, в результате получаем дерево. В обратную сторону, если добавить в дерево новое ребро, соединяющее любые две вершины, получим 1-дерево. Путь в дереве, соединяющий две конечные точки добавляемой дуги, вместе с самой добавляемой дугой, образует единственный цикл 1-дерева. Если добавить в 1-дерево ребро, соединяющее одну из вершин дерева с вновь образуемой вершиной, в результате опять получим 1-дерево с ещё одной вершиной. Другой метод построения 1-деревьев начинается с единичного цикла, и к 1-дереву последовательно добавляются вершины произвольное число раз. Рёбра любого 1-дерева можно разделить единственным образом на два подграфа, один из которых — цикл, а второй — лес, при этом каждое дерево леса содержит в точности одну вершину цикла [7]

Изучаются также несколько более узкие типы псевдолесов.

1-лес, называемый иногда максимальным псевдолесом, — это лес, к которому нельзя добавить ребро без образования графа с более чем одним циклом. Если псевдолес содержит дерево в качестве одной из компоненты, он не может быть 1-лесом, поскольку можно добавить к этой компоненте ребро с образованием цикла в этой компоненте или добавить ребро, которое присоединит дерево к другой компоненте. Таким образом, 1-леса — это в точности псевдолеса, в которых любая компонента является 1-деревом.

Остовный псевдолес неориентированного графа G — это остовный подграф, являющийся псевдолесом, т. е. псевдолес графа G, содержащий все вершины графа G. Такие псевдолеса не обязаны иметь какие-либо рёбра, поскольку, например, пустой подграф (т. е. содержащий все вершины графа G и не имеющий каких-либо рёбер) является псевдолесом (и его компонентами являются деревья, каждое из которых состоит из единственной вершины).

Максимальные псевдолеса графа G — это подграфы графа G, являющиеся псевдолесами, которые не содержатся в никаком большем псевдолесе, содержащемся в G. Максимальный псевдолес графа G всегда является остовным псевдодеревом, но обратное неверно. Если G не имеет связных компонент, являющихся деревьями, то его максимальные псевдолеса являются 1-лесами, но в случае, когда граф G содержит дерево в качестве компоненты, его максимальные псевдолеса не будут 1-лесами. Говоря точнее, в любом графе G его максимальные псевдолеса состоят из всех лесов графа G вместе с одним или более 1-деревом, покрывающим оставшиеся вершины графа G.

Версии этих определений используются также для ориентированных графов. Подобно неориентированным графам ориентированные графы состоят из вершин и рёбер, но каждое ребро имеет направление (ориентированное ребро обычно называется дугой). Ориентированный псевдолес — это ориентированный граф, в которой каждая вершина имеет максимум одну исходящую дугу. То есть граф имеет степень исхода, не превосходящую единицы. Ориентированный 1-лес, часто называемый функциональным графом (см ниже), а иногда — максимальным ориентированным псевдолесом, — это ориентированный граф, в котором каждая вершина имеет исходящую степень в точности равную единице [8]. Если D — ориентированный псевдолес, неориентированный граф, образованный удалением направлений из рёбер графа D, является неориентированным псевдолесом.

Любой псевдолес на множестве из n вершин имеет максимум n рёбер, а любой максимальный псевдолес на множестве из n вершин имеет в точности n вершин. В обратную сторону, если граф G имеет свойство, что для любого подмножества S вершин графа число рёбер в порождённом подграфе графа S не превосходит числа вершин графа S, то G является псевдолесом. 1-деревья могут быть определены как связные графы с одинаковым числом вершин и рёбер [2].

Для семейств графов, если семейство графов имеет свойство, что любой подграф графа в семействе входит в то же семейство и каждый граф в семействе имеет не больше рёбер, чем вершин, то семейство содержит только псевдолеса. Например, любой подграф трекла (граф, нарисованный таким образом, что любая пара рёбер имеет одну точку пересечения) является также треклом, так что гипотезу Конвея, что любой трекл имеет не больше рёбер, чем вершин, можно переформулировать, что каждый трекл является псевдолесом. Точнее, если гипотеза верна, то треклы — это в точности псевдолеса без циклов с четырьмя вершинами и максимум одним циклом с нечётным числом вершин [9][10].

Стрейну и Теран [11] обобщили свойства разреженности в определении псевдолесов — он определяют граф как (k,l)-разреженный, если любой непустой подграф с n вершинами имеет максимум kn − l рёбер, и (k,l)-плотным, если он (k,l)-разрежен и имеет в точности kn − l рёбер. Таким образом, псевдолеса — это (1, 0)-разреженные графы, а максимальные псевдолеса — это (1, 0)-плотные графы. Некоторые другие важные семейства графов можно определить для других значений k и l, и если l ≤ k, (k,l)-разреженные графы можно описать как графы, образованные объединением l лесов без общих рёбер и k − l псевдолесов [12].

Почти любой достаточно редкий случайный граф является псевдолесом [13]. То есть, если c является константой (0 < c < 1/2) и P_c(n) — вероятность, что выбранный случайно среди графов с n вершинами и cn рёбрами граф является псевдолесом, то P_c(n) стремится к единице в пределе при росте n. Однако для c > 1/2 почти любой случайный граф с cn рёбрами имеет большую компоненту, не являющуюся одноцикловой.

Граф является простым, если в нём нет петель и кратных рёбер. Число простых 1-деревьев с n помеченными вершинами равно[14]

${\displaystyle n\sum _{k=1}^{n}{\frac {(-1)^{k-1}}{k}}\sum _{n_{1}+\cdots +n_{k}=n}{\frac {n!}{n_{1}!\cdots n_{k}!}}{\binom {{\binom {n_{1}}{2}}+\cdots +{\binom {n_{k}}{2}}}{n}}.}$

Значения для n вплоть до 18 можно найти в последовательности A057500 Энциклопедии целочисленных последовательностей.

Число максимальных ориентированных псевдолесов с n вершинами, в которых разрешены петли, равно nⁿ, поскольку для любой вершины имеется n возможных конечных вершин исходящих дуг. Андрэ Жуайяль использовал этот факт для биективного доказательства [15] формулы Кэли, что число неориентированных деревьев на n вершинах равно n^n − 2, путём нахождения биекции между максимальными ориентированными псевдолесами и неориентированными деревьями с двумя различными вершинами[16]. Если допускаются петли, число максимальных ориентированных псевдолесов равно (n − 1)ⁿ.

Функция на множестве {0,1,2,3,4,5,6,7,8} на себя и соответствующий функциональный граф

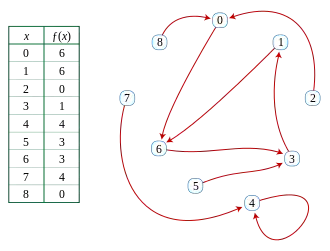
Ориентированные псевдолеса и отображения в себя в некотором смысле математически эквивалентны. Любое отображение ƒ на множестве X на себя (то есть эндоморфизм на X) можно интерпретировать как определение ориентированного псевдолеса, который имеет дугу из x в y, когда ƒ(x) = y. Полученный ориентированный псевдолес максимален и может включать петли, если для некоторых x ƒ(x) = x. Исключение петель приводит к немаксимальным псевлдолесам. В обратном направлении любой максимальный ориентированный псевдолес определяет отображение ƒ, для которой ƒ(x) равно конечной вершине дуги, исходящей из x, и любой немаксимальный ориентированный псевдолес можно сделать максимальным путём добавления петель и конвертирования в функцию тем же способом. По этой причине максимальные ориентированные псевдолеса иногда называются функциональными графами[2]. Представление функции в виде функционального графа даёт удобный язык описания свойств, которые непросто описать с точки зрения теории функций. Такая техника особенно полезна для задач, использующих итерированные функции, которые соответствуют путям в теории графов.

Поиск циклов, задача прослеживания путей в функциональном графе для нахождения в нём цикла, имеет приложения в криптографии и вычислительной теории чисел как часть ро-алгоритма Полларда для факторизации целых чисел и как метод нахождения конфликтов в криптографических хеш-функциях. В этих приложениях предполагается, что ƒ случайна. Флажоле и Одлыжко[17] изучали свойства функциональных графов, полученных из случайных отображений. В частности, из одного из вариантов парадокса дней рождения следует, что в случайном функциональном графе с n вершинами путь, начинающийся со случайно выбранной вершины, обычно зацикливается после O(√n) шагов. Конягин и др. осуществили анализ и вычислительные статистические исследования[18].

Мартин, Одлыжко и Вольфрам[19] исследовали псевдолеса, моделирующие динамику клеточных автоматов. Это функциональные графы, они назвали их диаграммами переходов состояний, имеют по одной вершине для каждой возможной конфигурации, в которой могут находиться ячейки клеточного автомата, а дуги соединяют каждую конфигурацию, которая из неё получается согласно правилам клеточного автомата. Можно получить свойства автомата из структуры этих диаграмм, такие как число компонент, длину конечных циклов, глубину деревьев, соединяющих неконечные состояния этих циклов, или симметрии диаграммы. Например, любая вершина без входящей дуги соответствует саду Эдема, а вершины с петлёй соответствуют натюрморту.

Другое раннее приложение функциональных графов — в цепочках[20], используемых для изучения систем троек Штейнера[21][22][23]. Цепочка системы троек является функциональным графом, содержащим по вершине для каждой возможной тройки символов. Каждая тройка pqr отображается функцией ƒ в stu, где pqs, prt и qru — тройки, принадлежащие системе троек и содержат пары pq, pr и qr соответственно. Было показано, что цепочки являются мощным инвариантом системы троек, хотя их вычисление громоздко.

Матроид — это математическая структура, в которой некоторые множества элементов определяются как независимые, в том смысле, что независимые множества удовлетворяют свойствам, которые моделируют свойства линейной независимости в векторном пространстве. Одним из стандартных примеров матроидов является графовый матроид, в котором независимые множества — это множества рёбер в лесах графа. Матроидная структура лесов важна для алгоритмов вычисления минимального остовного дерева графа. Аналогичным образом можно определить матроиды для псевдолесов.

Для любого графа G = (V,E), мы можем определить матроид на рёбрах графа G, в котором множество рёбер независимо тогда и только тогда, когда это множество образует псевдолес. Это матроид известен как бициклический матроид графа G [24][25]. Минимальные зависимые множества для этого матроида — это минимальные связные подграфы графа G, имеющие более одного цикла, и эти подграфы иногда называются бициклами. Существует три возможных типа бициклов — тета граф имеет две вершины, соединённых тремя путями, не имеющими внутренних общих точек, «восьмёрка» состоит из двух циклов, имеющих одну общую вершину, и «наручники» образованы двумя не имеющими общих вершин циклами, соединёнными путём [26]. Граф является псевдолесом тогда и только тогда, когда он не содержит бицикла в качестве подграфа[11].

«Бабочка» (слева) и алмаз (справа), запрещённые миноры псевдолесов

Образование минора псевдолеса путём стягивания некоторых рёбер и удаления некоторых других рёбер образует новый псевдолес. Таким образом, семейство псевдолесов замкнуто по минорам, а из теоремы Робертсона — Сеймура тогда следует, что псевдолеса можно описать в терминах конечного набора запрещённых миноров, аналогично теореме Вагнера описания планарных графов как графов, не имеющих ни полного графа K₅, ни полного двудольного графа K_3,3 в качестве миноров. Как обсуждалось ранее, любой граф, не являющийся псевдолесом, содержит в качестве подграфа «наручники», «восьмёрку» или «тета». Любые «наручники» и «восьмёрки» могут быть стянуты к «бабочке» («восьмёрка» с пятью вершинами), а любой граф «тета» может быть стянут к «алмазу» («тета»-граф с четырьмя вершинами) [27], так что любой граф, не являющийся псевдолесом, содержит либо «бабочку», либо «алмаз» в качестве минора, и только эти графы являются минимальными графами, не принадлежащими семейству псевдолесов. Если запретить только «алмаз», но не «бабочку», получим более широкое семейство графов, состоящее из «кактусов» и разрозненного объединения набора «кактусов» [28].

Если рассматривать мультиграфы с петлями, имеется только один запрещённый минор, вершина с двумя петлями.

Раннее алгоритмическое применение псевдолесов использовало алгоритм сетевого симплекса и его приложение к обобщённой задаче о потоках в сетях для моделирования преобразований продуктов из одного типа в другой[3][29]. В этих задачах задаётся транспортная сеть, в которой вершины моделируют каждый продукт, а рёбра моделируют допустимость преобразования из одного продукта в другой. Каждое ребро маркируется пропускной способностью (количество продукта, которое может быть преобразовано за единицу времени), потоком (скоростью преобразования между продуктами) и ценой (сколько теряем при преобразовании на единицу товара). Задачей является в определении, сколько каждого продукт нужно преобразовать на каждой дуге транспортной сети с целью минимизировать цену или максимизировать доход, не нарушая ограничения и не позволяя любому типу продукта остаться неиспользованным. Этот тип задач можно сформулировать как задачу линейного программирования и решить с помощью симплекс-метода. Промежуточные решения, получаемые из этого алгоритма, как и конечное оптимальное решение, имеют специальные структуры — каждая дуга транспортной сети или не используется, или использует максимальное значение пропускной способности, за исключением подмножества дуг, образующих остовный псевдолес транспортной сети, и на этом подмножестве дуг поток может принимать значение от нуля до максимальной пропускной способности. В этом приложении одноцикловые графы иногда называются также дополненными деревьями, а максимальные псевдолеса — дополненными лесами[29].

Задача о минимальном остовном псевдолесе использует нахождение остовного псевдолеса минимального веса в большем графе G с весами. Вследствие матроидной структуры псевдолесов максимальные псевдолеса с минимальным весом могут быть найдены с помощью жадных алгоритмов подобно задаче нахождения минимального остовного дерева. Однако Габов и Тарьян нашли для этого случая более эффективный подход с линейным временем[2].

Псевдодревесность графа G определяется по аналогии с древесностью как минимальное число псевдолесов, на которые можно разделить рёбра. Эквивалентно, это минимальное число k, такое, что граф G является (k, 0)-разреженным, или минимальное число k, такое что рёбрам графа G можно задать направления, так что полученный ориентированный граф будет иметь степень исхода, не превосходящую k. Вследствие матроидной структуры псевдолесов псевдодревесность можно вычислить за полиномиальное время [30]

Случайный двудольный граф c n вершинами на каждой его доле с cn рёбрами, выбранными случайно и независимо для каждой пары n² возможных пар вершин с большой вероятностью является псевдолесом при постоянном c строго меньшем единицы. Этот факт играет ключевую роль в анализе хеширования кукушки[31], структуре данных для поиска пар ключ-значение путём просмотра одной из двух хеш-таблиц на месте, определяемом ключом, — можно сформировать «парный граф», вершины которого соответствуют положению расположению в хеш-таблицах, а рёбра связывают два местоположения, в которых один из ключей можно найти. Парное хеширование находит все ключи тогда и только тогда, когда парный граф является псевдолесом[32].

Псевдолеса играют также ключевую роль в параллельных алгоритмах раскраски графов и связанных задач[33][34].

• Weisstein, Eric W. Unicyclic Graph (англ.) на сайте Wolfram MathWorld.