Полуикосаэдр
Полуикосаэдр — это абстрактный правильный многогранник, содержащий половину граней правильного икосаэдра. Он может быть реализован как проективный многогранник (мозаика проективной плоскости 10 треугольниками), который можно представить себе путём построения проективной плоскости как полусферы, противоположные точки которой вдоль границы соединены и делят полусферу на три равные части.
| Полуикосаэдр | ||
|---|---|---|
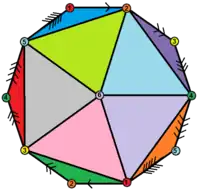 Десятиугольная диаграмма Шлегеля | ||
| Тип |
Абстрактный правильный многогранник проективный многогранник |
|
| Свойства |
неориентированный эйлерова характеристика = 1 |
|
| Комбинаторика | ||
| Элементы |
|
|
| Грани | 10 треугольников | |
| Конфигурация вершины | 3.3.3.3.3 | |
| Двойственный многогранник | полудодекаэдр | |
| Классификация | ||
| Символ Шлефли | {3,5}/2 or {3,5}5 | |
| Группа симметрии | A5, порядок 60 | |
Геометрия
Полуикосаэдр имеет 10 треугольных граней, 15 рёбер и 6 вершин.
Он также связан с невыпуклым однородным многогранником, тетрагемигексаэдром, который топологически идентичен полуикосаэдру, если 3 его квадратные грани разделить на треугольники.
Графы
Многогранник можно представить симметричным относительно граней и вершин диаграммой Шлегеля:
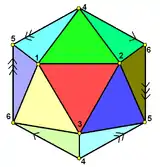 |
| Гранецентрированная диаграмма |
|---|
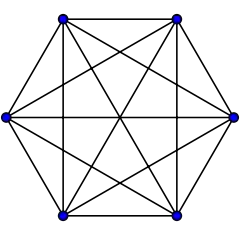
Полный граф K6
Многогранник имеет те же вершины и рёбра, что и пятимерный гексатерон, имеющий полный набор рёбер, но содержит только половину (20) граней.
С точки зрения теории графов это вложение графа (полный граф с 6 вершинами) в проективную плоскость. Для этого вложения двойственным графом будет граф Петерсена (см. полудодекаэдр).
См. также
- 11-ячейник – абстрактный правильный четырёхмерный многогранник, построенный из 11 hemi-icosahedra.
- полудодекаэдр
- Полукуб
- Полуоктаэдр
Литература
- Peter McMullen, Egon Schulte. 6C. Projective Regular Polytopes // Abstract Regular Polytopes. — Cambridge University Press, December 2002. — P. 162–165. — ISBN 0-521-81496-0.
