Подковообразная орбита
Подковообразная орбита — это один из типов коорбитального движения малого тела (астероида) относительно большого тела (планеты). Поскольку оба тела находятся практически на одинаковом расстоянии от Солнца, периоды обращения у них тоже почти полностью совпадают. В гелиоцентрической системе координат такая орбита вполне тривиальна и имеет вид обычной эллиптической орбиты Кеплера. Но если система координат вращается вокруг Солнца вместе с крупным телом (Землёй) и мы будем рассматривать относительно неё движение остальных тел системы, то малые тела (астероиды) будут двигаться вдоль так называемых поверхностей нулевых скоростей, некоторые из которых по форме напоминают подкову (отсюда и название этого типа орбит), между концами которой и будет располагаться более крупное тело (Земля). При этом данная подкова не будет располагаться неподвижно: сначала астероид будет медленно догонять Землю, до тех пор пока не приблизится к ней с одного из концов подковы, где в районе одной из троянских точек Лагранжа он резко изменит направление своего движения вследствие перехода на более высокую орбиту и начнёт понемногу отставать от Земли, до тех пор, пока они не сблизятся на другом конце подковы. В результате этого «подкова» будет как бы плавно дрейфовать относительного Земли из стороны в сторону вдоль её орбиты в течение длительного периода времени.
_2010_SO16_orbit.gif)
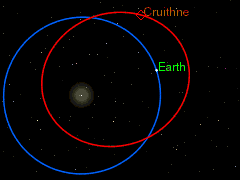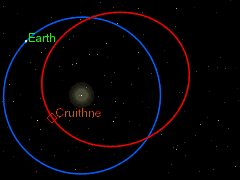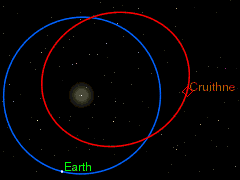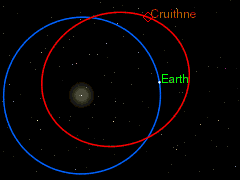
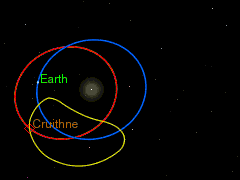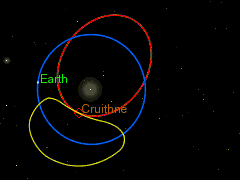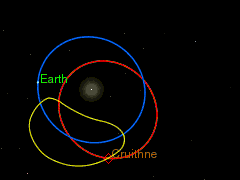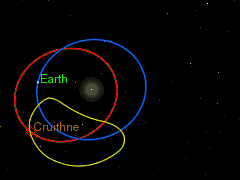
Одним из источников астероидов на подобных орбитах могут быть троянские астероиды. Если троянский астероид находится достаточно далеко от своей точки Лагранжа, то под действием даже относительно слабого возмущения со стороны какого-либо тела или из-за слишком большой, накопленной в результате резонанса, амплитуды колебаний на своей орбите он вполне может перейти на внешнее или внутреннее кольцо земной орбиты и начать двигаться по подковообразной орбите.
На данный момент открыто уже несколько астероидов, движущихся по столь необычным орбитам, в их числе такие астероиды как (54509) YORP, 2002 AA29, (3753) Круитни[1], 2010 SO16, (85770) 1998 UP1, 2003 YN107, 2014 YX49 (коорбитальный спутник Урана), а также недавно открытый астероид 2009 TK7 и, возможно, 2001 GO2.
Впрочем, подковообразные орбиты свойственны не только астероидам, но и малым спутникам планет-гигантов. В частности, в системе Сатурна по таким орбитам по отношению друг к другу движутся спутники Эпиметей и Янус (в их случае нет повторяющихся циклов, поскольку каждый находится на своей оконечности «подковы»).
Принцип движения
Общие положения
Далее в качестве примера будем рассматривать астероид, движущийся вокруг Солнца по подковообразной орбите рядом с Землёй. Астероид находится практически на том же расстоянии от Солнца, что и Земля и движется с нею в орбитальном резонансе 1:1, совершая один оборот вокруг Солнца за то же время, что и Земля (плюс-минус пару часов).
Чтобы понять принцип движения астероида на подковообразной орбите, нужно хорошо представлять два ключевых, для данного случая, правила орбитальной динамики:
- Чем ближе небесное тело находится к Солнцу, тем быстрее оно вращается вокруг него, и наоборот (третий закон Кеплера)
- Если тело ускоряется вдоль своей орбиты, её радиус увеличивается (при этом скорость движения по орбите уменьшается), и наоборот, если тело замедляется, то радиус орбиты снижается (при этом скорость движения по орбите увеличивается).
Подковообразная орбита возникает из-за искажения гравитационным полем Земли эллиптической орбиты астероида. Искажения эти очень малы, но они приводят к значительным изменения в движении астероида относительно Земли.
Подковообразное движение становится наиболее наглядным, если следить за движением астероида в геоцентрической системе отсчёта, то есть, считая Землю неподвижной и рассматривая движение астероида относительно неё. Астероид проходит весь цикл движения по своей орбите, не меняя своего направления движения, но тем не менее, то догоняя, то отставая от Земли. Так что, траектория его движения по форме немного напоминает подкову.
Этапы движения по орбите
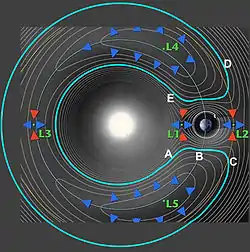
Предположим, что астероид находится на внутреннем кольце земной орбиты в точке «А» вблизи троянской точки L5. Период обращения астероида вокруг Солнца чуть меньше одного земного года. Поскольку астероид находится ближе к Солнцу, чем Земля, его орбитальная скорость выше и он догоняет Землю. Далее астероид приближается к Земле на достаточно близкое расстояние, где под влиянием земного гравитационного поля на астероид вдоль его орбиты начинает действовать внешняя ускоряющая сила, которая увлекает астероид на более высокую орбиту и вызывает приращение его скорости. Данный эффект увеличения скорости тела в гравитационном поле других планет широко используется для разгона земных космических аппаратов, направляемых для исследования внешних областей Солнечной системы. Но хотя сама скорость движения астероида увеличивается, значение орбитальной её составляющей вследствие перехода на более высокую орбиту падает. В точке «B» орбитальная составляющая скорости движения астероида снижается настолько, что становится равной орбитальной скорости Земли, и астероид некоторое время движется почти синхронно с нею. Но поскольку он по-прежнему находится в зоне действия земной гравитации, внешняя ускоряющая сила по-прежнему продолжает на него действовать, вызывая дальнейшее приращение скорости и переход на более высокую орбиту. Спустя ещё какое-то время астероид переходит на внешнее кольцо земной орбиты в точку «С», где его орбитальная скорость становится меньше орбитальной скорости Земли, и он начинает отставать от неё. Дальнейшие несколько сотен лет астероид проведёт спокойно двигаясь по своей орбите постепенно удаляясь от Земли со стороны точки L5 и приближаясь к ней со стороны точки L4. Период обращения астероида вокруг Солнца чуть больше одного земного года. В конце концов астероид догоняет Землю и оказывается с другой её стороны в точке «D» вблизи троянской точки L4. Как только астероид вновь входит в зону влияния земной гравитации, начинается процесс, обратный происходившему вблизи точки L5. Происходит торможение астероида, вследствие чего он начинается спускаться на более низкую орбиту. При этом его орбитальная скорость постепенно возрастает, пока астероид вновь не окажется на внутреннем кольце земной орбиты в точке «E». Из этой точки в течение ещё нескольких сотен лет он будет спокойно двигаться опережая Землю и всё сильнее удаляясь от неё, пока в какой-то момент времени вновь не окажется в точке «A», с которой цикл начнётся вновь.
Сохранение орбитальной энергии
Интересно рассмотреть движение астероида по подковообразной орбите с точки зрения закона сохранения энергии. Это теорема классической механики, которая гласит, что полная энергия тела движущегося в пространстве в зависимости от времени равна сумме кинетической (всегда положительной) и потенциальной (отрицательной) энергий этого тела:
Очевидно, что поскольку около тела с массой М (Земли) в связанной с ним системой отсчёта
- ,
то будет возрастать в области, расположенной за телом , и, наоборот, будет уменьшаться в области, расположенной перед этим телом. Несмотря на это, тела на низких орбитах с меньшей суммарной энергией имеют более короткие периоды обращения, так как тело, движущееся ближе к Солнцу будет терять энергию сдвигаясь на более низкую орбиту, с меньшим периодом обращения. Дело в том, что астероид теряет и получает энергию движения за счёт тяготения Земли. Поэтому, когда он, двигаясь по подковообразной орбите, догоняет Землю, то она притягивает астероид, добавляя ему ускорения, и перебрасывает его на внутреннюю орбиту, а когда тело движется оказывается перед Землёй, то она за счёт притяжения притормаживает его, уменьшая его ускорение, и перебрасывает его на внешнюю орбиту. Разность энергий между внутренней и внешней орбитами возникает за счёт орбитального движения Земли. Поэтому, тела находящиеся позади планеты, будут получать энергию и переходить на более быструю внутреннюю орбиту, догоняя Землю, а оказавшись перед нею, начнут терять энергию и переходить на более медленную внешнюю орбиту, отставая от Земли.
Орбиты-головастики
При уменьшении энергии тела середина подковы сужается и сходится к лагранжевой точке L3. При дальнейшем уменьшении энергии она разрывается на две части, называемые головастиками. При этом астероид оказывается заперт на одном из них. Движение тела по орбите-головастику происходит вокруг точек Лагранжа L4 и L5 (на рисунке орбита головастика выделена синими треугольниками). Астероид колеблется вокруг одной из троянских точек между Землёй и точкой L3. Движение тела по данной орбите объясняется аналогичным образом. В зависимости от того, приближается тело к Земле или удаляется от неё, гравитационное поле Земли приводит либо к ускорению, либо к замедлению скорости движения тела, попутно меняя направление его движения по орбите относительно Земли, вызывая то самое вращательное движение вокруг одной из троянских точек[2]. По мере уменьшения энергии астероида размер головастика уменьшается, пока он не стягивается в лагранжеву точку L4 или L5.
Яркими примерами тел, движущихся по таким орбитам, являются спутники Сатурна — Полидевк и Елена.
Примечания
- Apostolos A. Christou, David J. Asher. «A long-lived horseshoe companion to the Earth», arXiv, arXiv:1104.0036v1
- S.M. Giuliatti Winter, O.C. Winter, D.C. Mourão. Peculiar trajectories around the Lagrangian equilateral points. Дата обращения: 8 декабря 2009.
Ссылки
- Сложные семейства периодических решений ограниченной задачи (англ.)
- Research paper describing Horseshoe orbits (англ.)
- A good description of 2002 AA29
- Artikel über Hufeisenorbits (англ.)
- GIF-Animationen der Bahnbewegungen der Erde und des Asteroiden 2002 AA29 Архивная копия от 19 сентября 2009 на Wayback Machine (англ.)