Нормальная высота
Нормальная высота — один из возможных способов определения высоты от уровня моря. Величина, численно равная отношению геопотенциальной величины в данной точке к среднему значению нормальной силы тяжести Земли по отрезку, отложенному от поверхности земного эллипсоида[1].
Иначе, значение, которое можно охарактеризовать как: перемещение единичной массы в поле силы тяжести из некоторой точки с потенциалом в точку с потенциалом , деленное на среднее интегральное значение нормальной силы тяжести на отрезке до . В отличие от ортометрической высоты при вычислении нормальной высоты нет необходимости иметь информацию о внутреннем строении Земли, так как вычисление нормальной высоты происходит не в реальном, а в нормальном поле[2].
Общая информация
История введения термина
Впервые нормальные высоты введены[3] М. С. Молоденским, тогда они ещё не имели названия и были обозначены через [4]. В работе того же Молоденского, нормальные высоты были названы вспомогательными[5]. Свое современное название эти высоты, по предложению Молоденского, получили в работе В.Ф. Ермеева[6]
М. С. Молоденский отметил, что определение малой разности между реальным и нормальным гравитационным полем Земли (аномальное поле) имеет строгое решение, если в возникающих уравнениях ввести «вспомогательные» высоты под условием:
В. Ф. Еремеев отметил, что «вспомогательные» высоты ближе к суммам нивелирных превышений, чем ортометрические высоты, и по предложению самого Молоденского был введён термин «нормальная высота»[7].
Связь с Балтийской системой высот
При измерении нивелирных превышений и вычислении геопотенциальных чисел в разных странах используют различные исходные пункты. Каждая изолированная нивелирная сеть, развитая от какого-либо футштока, определяет разности потенциалов точек этой сети относительно уровненной поверхности , проходящей через исходный пункт данной сети. Поскольку уровень моря в разных районах различен, исходные пункты связаны с разными уровенными поверхностями, и по измерениям в изолированных сетях нельзя получить геопотенциальные числа для всей Земли в единой системе. Чтобы подчеркнуть это, говорят, что на данной территории развита система высот от определённого футштока. Так, в СССР была создана Балтийская система высот, в которой исходным пунктом служит Кронштадский футшток. Здесь термин «система» имеет смысл, как система, которая устанавливает некоторую уровенную поверхность, относительно который вычисляют разности потенциалов[8].
Использование в других странах
Система нормальных высот принята в России, странах СНГ и некоторых европейских странах, Швеция, Германия, Франция и др.).
В Австрии, Боснии и Герцеговине, Норвегии, Югославии приняты нормально-ортометрические высоты[8].
Особенности использования термина
В случаях, когда высоты определены с не очень высокой точностью, все высоты, кроме геодезической, называют высотами над уровнем моря, или абсолютными высотами, а разность высот — относительными высотами. Это аналогично названию координат приближенно все координаты (астрономические, геодезические, геоцентрические) называют географическими[8].
Способы определения
- Геометрическое нивелирование
- Спутниковое нивелирование
Основные сведения
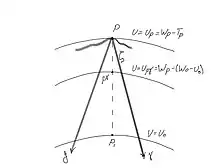
Натуральная система координат связана с силовыми линиями и уровенными поверхностями реального поля Земли. Система координат в нормальном поле связана с нормальной силовой линией и нормальной уровенной поверхностью, проходящими через данных пункт. Так как нормальное поле не совпадает с действительными, координаты в нормально поле отличаются от натуральных[9].
Связь с геопотенциальным числом
Установим связь нормального геопотенциального числа с действительным . Для потенциала в точке
;
образуем разность . Учитывая что эта разность равна аномальному потенциалу получим
Действительное и нормальное геопотенциальное число различается на величину аномального потенциала в точке и разность потенциалов на геоиде и уровенном эллипсоиде.
Если бы гравитационное поле Земли совпадало с нормальным и потенциал на геоиде был равен потенциалу на уровенном эллипсоиде, нормальное и действительное геопотенциальное число точки тоже совпали бы. Однако на силовой линии нормального поля, проходящей через точку , всегда найдется такая точка в которой нормальное геопотенциальное число тождественно равно действительному
Причем поскольку нормальный потенциал всегда выбирают близким к действительному, точка будет не далеко расположена от точки [9].
Отличие от высоты в нормальном поле
Высота в нормальном поле определена как отрезок нормальной силовой линии от эллипсоида до любой точки . Она отличается от геодезической высоты только из-за кривизны нормальной силовой линии, но это отличие практически не ощутимо. Высота в нормальном поле — это расстояние, измеряемое вдоль силовой линии нормального поля от эллипсоида до любой точки , а нормальная высота — расстояние вдоль нормальной силовой линии от той же точки эллипсоида, но не до точки , а до точки , в который выполняется тождество выше[9].
Связь с аномалией высоты
Отрезок появляется из-за несовпадения действительного и нормального поля является элементом аномального поля. Его называют аномалией высоты.
Аномалию высоты получают как расстояние между уровенными поверхностями проходящими через точки и . Согласно формуле , полагая и , находим
где — среднее значение нормальной силы тяжести на отрезке [9]
Связь с геодезической высотой
Высота равна сумме нормальной высоты и аномалии высоты
Так как высота в нормальном поле практически совпадает с геодезической, это выражение справедливо и для связи геодезической и нормальной высот
Основная формула
Перенесём измеренную разность потенциалов в нормальное поле:
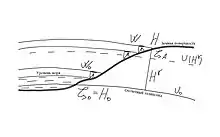
где точка с нормальным потенциалом не совпадает с точкой H на земной поверхности, а лежит с ней практически на одной нормали к эллипсоиду (см. рис. 1), — среднее интегральное значение нормальной силы тяжести на отрезке от до :
что можно вычислить с любой степенью точности, в отличие от грубо известного , где — среднее интегральное значение силы тяжести на отрезке силовой линии. Из условия выше имеем:
|
— нормальная высота точки земной поверхности. |
В простейшем случае можно определить по нормальному градиенту как на половине , то есть[2]:
Примечания
- ГОСТ 22268-76: Геодезия. Термины и определения. Термин № 29
- Попадьёв В. В. Основы геодезической гравиметрии и теоретической геодезии (курс лекций). — М.: МИИГАиК, 2018, 160 с., с.110-114
- Молоденский М. С. Основные вопросы геодезической гравиметрии. Тр. ЦНИИГАиК, 1945, вып. 42, 107 стр.
- Eремеев В. Ф.‚ Юркина М. И. Теория высот в гравитационном поле Земли. М., «Недра», 1971, с. 33 сноска
- Молоденский М. С. Внешнее гравитационное поле и фигура физической поверхности Земли. Изв. АН СССР, серия географ. и геофиз. 1948, 12, N9 3, 193—211.
- Еремеев В. Ф. Теория ортометрических, динамических и нормальных высот. Тр. ЦНИИГАиК, 1951, вып. 86, 11-51.
- Гравитационное поле, фигура и внутреннее строение Земли. — М.: Наука, 2001. — 569 с.; ил. (Серия «Избранные труды»). ISBN 5-02-002331-0
- Огородова Л.В. Высшая геодезия. Часть III. Теоретическая геодезия. — Москва: Геодезкартиздат, 2006. — С. 217—218. — 384 с. — ISBN 5-86066-076-6.
- Огородова Л.В. Высшая геодезия. Часть III. Теоретическая геодезия. — Москва: Геодезкартиздат, 2006. — С. 106—110. — 384 с. — ISBN 5-86066-076-6.