Многочлены Цернике
Многочлены Цернике — последовательность многочленов, которые являются ортогональными на единичном круге. Названы в честь лауреата Нобелевской премии, оптика и изобретателя фазово-контрастного микроскопа Фрица Цернике. Они играют важную роль в оптике[1].
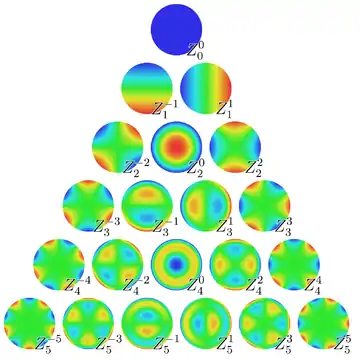
Определения
Есть чётные и нечётные многочлены Цернике. Чётные многочлены определены как
- ,
а нечётные как
- ,
где m и n — неотрицательные целые числа, такие что n≥m, φ — азимутальный угол, а ρ — радиальное расстояние, . Многочлены Цернике ограничены в диапазоне от −1 до +1, т.е. .
Радиальные многочлены определяются как
для чётных значений n − m , и тождественно равны нулю для нечётных n − m .
Другие представления
Переписав дробь с факториалами в радиальной части в виде произведения биномиальных коэффициентов, можно показать, что коэффициенты при степенях суть целые числа:
- .
Для выявления рекуррентностей, для демонстрации того факта, что эти многочлены являются частным случаем многочленов Якоби, для записи дифференциальных уравнений и т.д., используется запись в виде гипергеометрических функций:
для четных значений n − m.
Свойства
Ортогональность
Ортогональность в радиальной части записывается равенством
Ортогональность в угловой части представляется набором равенств
где параметр (его иногда называют множителем Неймана) полагают равным 2, если , и равным 1, если . Произведение угловой и радиальной частей устанавливает ортогональность функций Цернике по обеим переменным при интегрировании по единичному кругу:
где — якобиан полярной системы координат, а оба числа и — четные.
Примеры
Радиальные многочлены
Ниже представлены несколько первых радиальных многочленов.
См. также
Примечания
- Zernike, F. Beugungstheorie des Schneidenverfahrens und Seiner Verbesserten Form, der Phasenkontrastmethode (нем.) // Physica I : magazin. — 1934. — Bd. 8. — S. 689—704.