Многоугольник видимости
Многоугольник видимости или область видимости для точки p на плоскости среди препятствий — это (возможно неограниченная) многоугольная область всех точек плоскости, видимых из точки p. Многоугольник видимости можно определить для видимости из отрезка или многоугольника. Многоугольники видимости полезны в робототехнике, компьютерных играх и для определения позиций объектов, например, для определения наилучшего расположения охраны в картинных галереях.
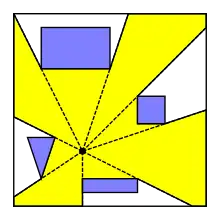
Если многоугольник видимости ограничен, то он является звёздчатым многоугольником. Многоугольник видимости ограничен, если все лучи, проведённые из точки, в конце концов, обрываются на некотором препятствии. Это случается, например, когда препятствия являются рёбрами простого многоугольника, а точка p находится внутри многоугольника. В таком случае многоугольник видимости может быть найден за линейное время[1][2][3][4].
Определения
Формально мы можем определить задачу о планарном многоугольнике видимости следующим образом. Пусть будет набором препятствий (отрезки, либо многоугольники) в . Пусть будет точкой в , не находящейся внутри препятствия. Тогда многоугольник видимости точки — это множество точек в , таких, что для любой точки из отрезок не пересекает какой-либо объект из набора .
Аналогично, многоугольник видимости отрезка или многоугольник видимости ребра — это точки, видимые с любого места отрезка.
Приложения
Многоугольники видимости полезны в робототехнике. Например, в ориентации робота робот использует датчики, такие как лидар, которые обнаруживают препятствия, и область видимости аналогична многоугольнику видимости[5].
Они также полезны в компьютерных играх, и имеются многочисленные онлайновые учебные курсы, которые объясняют простые алгоритмы для реализации в играх[6][7][8].
Алгоритмы для точек видимости многоугольников
Было предложено много алгоритмов вычисления многоугольника видимости для точки. Для различных вариантов задачи (то есть различных видов препятствий) алгоритмы могут отличаться по времени и сложности.
Наивные алгоритмы
Наивные алгоритмы легко понять и реализовать, но они не оптимальны, поскольку они могут быть существенно медленнее других алгоритмов.
«Физический» алгоритм равномерного проведения лучей
В реальной жизни светящаяся точка освещает область, видимую из точки, поскольку точка излучает свет во всех направлениях. Это можно смоделировать путём проведения лучей во многих направлениях. Предположим, что имеется точка и набор препятствий . Тогда псевдокод может быть выражен следующим образом:
Алгоритм простой_плохой_алгоритм(, ) := для : // проводим луч с углом with angle := для каждого препятствия из : := min(, расстояние от до препятствия в этом направлении) добавляем вершину в возвращаем
Теперь, если была бы возможность просмотреть бесконечно много углов, результат был бы правильным. К сожалению, невозможно просмотреть все возможные направления ввиду ограничений компьютеров. Можно создать приближение путём проведения, скажем, 50 лучей равномерно. Однако это не точное решение, поскольку препятствия могут быть пропущены между двумя соседними лучами. Более того, алгоритм очень медленный, поскольку нужно проводить много лучей, а выходной многоугольник видимости может иметь много больше вершин, чем необходимо.
Проведение луча в каждую вершину
Описанный выше алгоритм может быть существенно улучшен как по скорости, так и по корректности путём наблюдения, что достаточно проводить лучи только к вершинам препятствий. Это потому, что любое огибание угла препятствия вдоль границы многоугольника видимости должно быть в некоторой угловой вершине препятствия.
Алгоритм простой_улучшенный_алгоритм(, ) := для каждого препятствия из : для каждой вершины of : // проводим луч из в := расстояние от до := угол of с для каждого препятствия из : := min(, расстояние от до ) добавляем вершину в возвращаем
Временная сложность алгоритма равна . Это потому, что алгоритм проводит луч в каждую из вершин и проверяет, где обрывается луч. Алгоритм должен проверить пересечение с каждым из препятствий. Это достаточно для многих простых приложений, таких как компьютерные игры и многие онлайновые обучающие курсы учат этому методу[8]. Однако, как мы можем видеть далее, существуют более быстрые алгоритмы со скоростью работы (или даже быстрее, если препятствие является простым многоугольником или имеется фиксированное число многоугольных дыр).
Оптимальные алгоритмы для точек в простом многоугольнике

Если дан простой многоугольник и точка , алгоритм линейного времени является оптимальным для вычисления области , которая видна из точки . Такой алгоритм был предложен в 1981[2]. Однако он довольно сложен. В 1983 был предложен концептуально более простой алгоритм[3], но он имел небольшую ошибку, которая была исправлена в 1987[4].
Последний упомянутый алгоритм будет кратко изложен здесь. Он просто проходит границу многоугольника , последовательно перебирая вершины, и хранит стек вершин , где — вершина стека. Стек состоит из вершин, видимых из . Если потом обнаружатся вершины, которые закрывают часть , то закрытые вершины выталкиваются из стека . Алгоритм прекращает работу, когда состоит из всех видимых вершин, то есть из желаемого многоугольника видимости. Эффективная реализация была опубликована в 2014[9].
Оптимальные алгоритмы для точек многоугольника с дырами
Для точки в многоугольнике с дырами и вершинами (в сумме) можно показать, что в худшем случае алгоритм оптимален. Такой алгоритм был предложен в 1995 вместе с доказательством его оптимальности[10]. Однако этот алгоритм опирается на алгоритм линейного времени триангуляризации многоугольника Чазелле, который крайне сложен.
Отрезки, которые могут пересекаться только на концах

Для точки среди множества из отрезков, которые могут пересекаться только на их концах, можно показать, что в худшем случае алгоритм со временем работы оптимален. Это потому, что алгоритм многоугольника видимости должен выводить вершины многоугольника видимости в отсортированном порядке, а следовательно, задача сортировки может быть сведена к вычислению многоугольника видимости[11].
Заметим, что любой алгоритм, который вычисляет многоугольник видимости, для точки среди отрезков может быть использован для вычисления многоугольника видимости для всех видов многоугольных препятствий, поскольку многоугольник может быть разбит на отрезки.
Разделяй и властвуй
Алгоритм «Разделяй и властвуй» для вычисления многоугольника видимости был предложен в 1987[12].
Угловое выметание
Угловое выметание, то есть вращательный алгоритм выметающей прямой для вычисления многоугольника видимости был предложен в 1985[13] и 1986[11]. Идея заключается в начальной сортировке концов отрезков по углу, а затем просмотре отсортированных точек. Во время итерирования события обрабатываются как куча. Эффективная реализация была опубликована в 2014[9].
Произвольно пересекающиеся отрезки
Для точки среди отрезков, пересекающихся произвольным образом, задача о многоугольнике видимости сводится за линейное время к задаче о нижней огибающей. Согласно доводам Дэвенпорта — Шинцеля вычисление нижней огибающей в худшем случае имеет сложность от числа вершин, где — обратная функции Аккермана. Оптимальный в худшем случае алгоритм «разделяй и властвуй», работающий за время , создал Джон Хершбергер в 1989[14].
Ссылки
- https://web.archive.org/web/20170503033619/http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en (видимость в простых многоугольниках — апплеты)
Программное обеспечение
- VisiLibity: A free open source C++ library for visibility computations in planar polygonal environments.
- visibility-polygon-js: A public domain Javascript library for computing многоугольник видимости for a point among segments using the Угловое выметание method.
Примечания
- Preparata, Shamos, 1985.
- El Gindy, Avis, 1981, с. 186–197.
- Lee, 1983, с. 207–221.
- Joe, Simpson, 1987, с. 458–473.
- Guibas, Motwani, Raghavan, 1992.
- Liow, 2014.
- Patel, 2012a.
- Patel, 2012b.
- Bungiu, Hemmer, Hershberger, Huang, Kröller, 2014.
- Heffernan, Mitchell, 1995, с. 184–201.
- Suri, O'Rourke, 1986, с. 14–23.
- Arkin, Mitchell, 1987.
- Asano, 1985, с. 557–559.
- Hershberger, 1989, с. 169–174.
Литература
- Franco P. Preparata, Michael Ian Shamos. Computational Geometry - An Introduction. — Springer-Verlag, 1985. — ISBN 0-387-96131-3 1st edition.
- Русский перевод: Препарата Ф., Шеймос М. Вычислительная геометрия: Введение. — М., 1989. — ISBN 5-03-001041-6 ББК 22.19 П72 УДК 681.3 513.
- Hossam El Gindy, David Avis. A linear algorithm for computing the visibility polygon from a point // Journal of Algorithms. — 1981. — Т. 2, вып. 2. — С. 186–197. — doi:10.1016/0196-6774(81)90019-5.
- Lee D. T. Visibility of a simple polygon // Computer Vision, Graphics, and Image Processing. — 1983. — Май (т. 22, вып. 2). — С. 207–221. — doi:10.1016/0734-189X(83)90065-8.
- Barry Joe, Simpson R. B. Corrections to Lee's visibility polygon algorithm // BIT Numerical Mathematics. — 1987. — Т. 27, вып. 4. — С. 458–473. — doi:10.1007/BF01937271.
- Leonidas Guibas, Rajeev Motwani, Prabhakar Raghavan. The robot localization problem in two dimensions // ACM-SIAM symposium on Discrete algorithms. — Society for Industrial and Applied Mathematics, 1992.
- Nicklaus Liow. SIGHT & LIGHT how to create 2D visibility/shadow effects for your game. — 2014.
- Amit Patel. 2d Visibility Algorithm. — 2012a. — Июль.
- Amit Patel. Blobs in Games: 2d Visibility. — 2012b. — Июль.
- Paul Heffernan, Joseph Mitchell. An optimal algorithm for computing visibility in the plane // SIAM Journal on Computing. — 1995. — Т. 24, вып. 1. — С. 184–201. — doi:10.1137/S0097539791221505.
- Subhash Suri, Joseph O'Rourke. Worst-case optimal algorithms for constructing visibility polygons with holes. — ACM, 1986. — С. 14–23. — doi:10.1145/10515.10517.
- Esther Arkin, Joseph S. B. Mitchell. An optimal visibility algorithm for a simple polygon with star-shaped holes. — Cornell University Operations Research and Industrial Engineering, 1987.
- Tetsuo Asano. An efficient algorithm for finding the visibility polygon for a polygonal region with holes. // =Institute of Electronics, Information, and Communication Engineers. — 1985. — Т. 68. — С. 557–559.
- Francisc Bungiu, Michael Hemmer, John Hershberger, Kan Huang, Alexander Kröller. Efficient Computation of Visibility Polygons. — 2014. — arXiv:1403.3905.
- John Hershberger. Finding the upper envelope of line segments in time // Information Processing Letters. — 1989. — Т. 33. — С. 169–174. — doi:10.1016/0020-0190(89)90136-1.