Последовательность Дэвенпорта — Шинцеля

Говорят, что конечная последовательность U=u₁, u₂, u₃ является последовательностью Дэвенпорта — Шинцеля порядка s, если она удовлетворяет следующим двум свойствам:

1. Никакие два последовательных значения в последовательности не равны друг другу.
2. Если x и y — два различные значения, появляющиеся в последовательности, то последовательность не содержит подпоследовательность … x, … y, …, x, …, y, … состоящую из s + 2 чередующихся значений x и y.

Например, последовательность

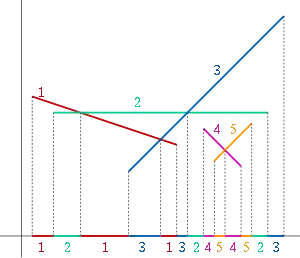
1, 2, 1, 3, 1, 3, 2, 4, 5, 4, 5, 2, 3

является последовательностью Дэвенпорта — Шинцеля порядка 3 — она содержит чередующаяся последовательность длины четыре, такую как …1, … 2, … 1, … 2, … (появляется четырьмя разными способами как последовательность полной последовательности), но она не содержит подпоследовательности длины пять.

Если последовательность Дэвенпорта — Шинцеля порядка s включает n различных значений, она называется (n,s) последовательностью Дэвенпорта — Шинцеля, или DS(n,s)- последовательностью [3].

Сложность DS(n,s)-последовательности анализируется асимптотически при n, стремящемся к бесконечности, в предположении, что s является константой и известны почти точные границы для всех s. Пусть λ_s(n) обозначает длину самой длинной DS(n,s)-последовательности. Лучшие известные границы λ_s используют обратную функцию Аккермана

α(n)=min { m|A(m,m) ≥ n },

где A — функция Аккермана. Ввиду очень быстрого роста функции Аккермана её обратная растёт очень медленно и не превосходит 4 для большинства задач любого практического размера[4].

Если использовать обозначение «O» большое, известны следующие границы:

• ${\displaystyle \lambda _{0}(n)=1}$.
• ${\displaystyle \lambda _{1}(n)=n}$[5]
• ${\displaystyle \lambda _{2}(n)=2n-1}$[5].

${\displaystyle \lambda _{3}(n)=2n\alpha (n)+O(n)}$[6][7][8][9][10][11] [12]. Эта граница сложности может быть реализована с точностью до константы отрезками — существует такое расположение n отрезков на плоскости, нижняя огибающая которых имеет сложность Ω(n α(n)) [13][8].

• ${\displaystyle \lambda _{4}(n)=\Theta (n2^{\alpha (n)})}$[14][15][12].
• ${\displaystyle \lambda _{5}(n)=\Theta (n\alpha (n)2^{\alpha (n)})}$[12].

• Для чётных и нечётных значений s ≥ 6

${\displaystyle \lambda _{s}(n)=n\cdot 2^{{\frac {1}{t!}}\alpha (n)^{t}+O(\alpha (n)^{t-1})}}$, где ${\displaystyle t=\left\lfloor {\frac {s-2}{2}}\right\rfloor }$[14][15][12].

Значение λ_s(n) также известно, если s переменна, а n — малая константа[16]:

${\displaystyle \lambda _{s}(1)=1\,}$

${\displaystyle \lambda _{s}(2)=s+1\,}$

${\displaystyle \lambda _{s}(3)=3s-2+(s\,{\bmod {\,}}2)}$

${\displaystyle \lambda _{s}(4)=6s-2+(s\,{\bmod {\,}}2).}$

Если s является функцией от n, верхняя и нижняя граница последовательности Дэвенпорта — Шинцеля не являются точными.

• Если ${\displaystyle s>n^{1/t}(t-1)!}$, ${\displaystyle \lambda _{s}(n)=\Omega (n^{2}s/(t-1)!)}$ и ${\displaystyle \lambda _{s}(n)=O(n^{2}s)}$[16][17].
• Если ${\displaystyle \log \log n<s=n^{o(1)}}$, ${\displaystyle \lambda _{s}(n)=\Omega \left(n\left({\frac {s}{2\log \log _{s}n}}\right)^{\log \log _{s}n}\right)}$[17].
• Если ${\displaystyle s\leq \log \log n}$, ${\displaystyle \lambda _{s}(n)=\Omega (n2^{s})}$[17].

Последовательность Дэвенпорта — Шинцеля порядка 3, образованная нижней огибающей отрезков.

Нижняя огибающая множества функций ƒ_i(x) от вещественной переменной x является функцией, заданной поточечным минимумом:

ƒ(x) = min_iƒ_i(x).

Предположим, что эти функции имеют очень хорошее поведение — они все непрерывны и любые две из них равны максимум в s значениях. При этих предположениях вещественную ось можно разбить на конечное число промежутков, внутри каждого из которых одна функция имеет значения, меньшие, чем значения всех других функций. Последовательность таких интервалов, помеченных минимальной функцией внутри каждого интервала, образует последовательность Дэвенпорта — Шинцеля порядка s. Таким образом, любая верхняя граница сложности последовательности Дэвенпорта — Шинцеля с этим порядком также ограничивает число интервалов в таком представлении нижней огибающей.

В оригинальном приложении Дэвенпорта — Шинцеля рассматривались функции, являющиеся различными решениями одного и того же однородного линейного дифференциального уравнения порядка s. Любые два различных решения имеют не более s общих значений, так что нижняя огибающая множества n различных решений образует DS(n,s)-последовательность.

Та же концепция нижней огибающей может быть применена к функциям, которые только кусочно непрерывны или определены только на интервалах вещественной оси. Однако в этом случае точки разрывности функций и концы интервалов, в которых каждая функция задана, добавляются к последовательности. Например, невертикальный отрезок на плоскости можно интерпретировать как график функции, отображающей точки x интервала в соответствующие значения y, и нижняя огибающая набора отрезков образует последовательность Дэвенпорта — Шинцеля порядка три, поскольку любые два отрезка могут образовать перемежающуюся последовательность длины, не превосходящей 4.

• Бесквадратное слово

• Davenport-Schinzel Sequence, from MathWorld.
• Davenport-Schinzel Sequences, a section in the book Motion Planning, by Steven M. LaValle.