Критерий Поста
Критерий Поста — одна из центральных теорем в теории булевых функций, устанавливающая необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию. Впервые сформулирован американским математиком Эмилем Постом.
В середине 60-х годов почти одновременно в СССР и во Франции появились работы, где с иных позиций и в более доступной форме излагались результаты Поста. В 80-е годы сразу целому ряду исследователей с использованием различных подходов и различной техники удалось получить достаточно компактные доказательства результатов Поста. Алгебраический подход в изучении замкнутых классов булевых функций (подалгебр итеративной алгебры Поста над множеством ) принадлежит А. И. Мальцеву.
Алгебра Поста и замкнутые классы
Булева функция — это функция типа , где , а — арность. Количество различных функций арности равно , общее же количество различных булевых функций бесконечно. Вместе с тем, очевидно, что многие функции могут быть выражены через другие с использованием оператора суперпозиции. Например, давно известно, что из дизъюнкции и отрицания можно, используя законы де Моргана, получить конъюнкцию. Кроме того, любая булева функция (за исключением тождественного нуля) может быть представлена в виде ДНФ, то есть, в терминах конъюнкции, дизъюнкции и отрицания. Возникает естественный вопрос: как определить, будет ли данный набор функций достаточным, чтобы представить любую булеву функцию? Такие наборы называются функционально полными. Теорема Поста даёт ответ на этот вопрос. Поскольку условие теоремы является необходимыми и достаточным, её называют также критерием.
Идея теоремы состоит в том, чтобы рассматривать множество всех булевых функций как алгебру относительно операции суперпозиции. Сейчас она носит имя алгебра Поста. Эта алгебра содержит в качестве своих подалгебр множества функций, замкнутых относительно суперпозиции. Их называют ещё замкнутыми классами. Пусть — некоторое подмножество . Замыканием множества называется минимальная подалгебра , содержащая . Иными словами, замыкание состоит из всех функций, которые являются суперпозициями . Очевидно, что будет функционально полно тогда и только тогда, когда . Таким образом, вопрос, будет ли данный класс функционально полон, сводится к проверке того, совпадает ли его замыкание с .
Оператор является оператором замыкания. Иными словами, он обладает (среди прочих) свойствами:
- (экстенсивность)
- (монотонность)
- (идемпотентность)
Говорят, что множество функций порождает замкнутый класс (или класс порождается множеством функций ), если . Множество функций называется базисом замкнутого класса , если и для любого подмножества множества , отличного от .
Если к подалгебре , не совпадающей с прибавить один элемент, ей не принадлежащий, и образовать замыкание, результатом будет новая подалгебра, содержащая данную. При этом, она совпадёт с , в том и только в том случае, если между исходной подалгеброй, и нет никаких других подалгебр, то есть, если исходная подалгебра была максимальной. Таким образом, для того, чтобы проверить, что данное множество функций функционально полно, достаточно убедиться, что оно не входит целиком ни в одну из максимальных подалгебр . Оказывается, что таких подалгебр всего пять, и вопрос принадлежности к ним может быть решён просто и эффективно.
Двойственность, монотонность, линейность. Критерий полноты
Ниже приведены некоторые следствия, вытекающие из теорем о двойственных функциях.
- Если — замкнутый класс, то — также замкнутый класс.
- Множество образует замкнутый класс.
- Если , то . В частности, если — базис класса , то — базис класса .
Перейдем теперь к выяснению полноты конкретных наборов функций.
Основные классы функций:
- Функция называется сохраняющей ноль, если . Класс таких функций называется .
- Функция называется сохраняющей единицу, если . Класс таких функций называется .
- Функция называется самодвойственной, если на противоположных наборах она принимает противоположные значения, то есть для самодвойственной функции выполняется тождество . Класс таких функций называется .
- Функция называется монотонной: . Класс таких функций называется .
- Функция называется линейной, когда её можно представить полиномом Жегалкина первой степени, то есть . Класс таких функций называется .
Теорема о замкнутости основных классов функций
Отметим, что ни один из замкнутых классов целиком не содержится в объединении остальных четырёх. Это вытекает из следующих соотношений:
|
Формулировка критерия
|
То есть когда в ней можно реализовать пять функций: несамодвойственную, немонотонную, нелинейную, не сохраняющую 0 и не сохраняющую 1.
Доказательство
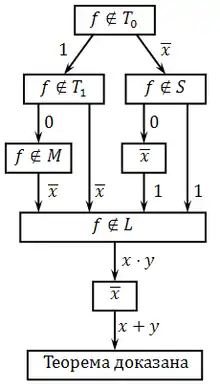
Доказательство критерия Поста основано на том, что система функций (И, ИЛИ и НЕ) является полной. Таким образом, любая система, в которой реализуемы эти три функции, также является полной. Докажем, что в системе, удовлетворяющей критерию Поста, всегда можно реализовать конъюнкцию, дизъюнкцию и отрицание.
Имея функцию, не сохраняющую 0, получим инвертор или константу 1
Рассмотрим функцию, не принадлежащую классу Т0. Для неё
Эта функция может принадлежать, а может не принадлежать классу Т1.
- В первом случае тогда и мы имеем константу единицы.
- Во втором случае тогда и мы имеем инвертор.
Имея функцию, не сохраняющую 1, получим инвертор или константу 0
Рассмотрим функцию, не принадлежащую классу Т1. Для неё
Эта функция может принадлежать, а может не принадлежать классу Т0.
- В первом случае тогда и мы имеем константу нуля.
- Во втором случае тогда и мы имеем инвертор.
Имея инвертор и несамодвойственную функцию, получим одну из констант
Рассмотрим функцию, не принадлежащую классу S самодвойственных функций. Для неё найдётся такой набор входных переменных X, что
Пусть, например, тогда и мы имеем константу 1.
Аналогично, если, например, тогда и мы имеем константу 0.
В любом случае, имея инвертор и несамодвойственную функцию мы можем получить одну из констант.
Имея инвертор и одну из констант, получим другую константу
Если в одном из вышеперечисленных случаев мы получили инвертор и одну из констант, вторую константу получим с помощью инвертора: или
Имея немонотонную функцию и обе константы, получим инвертор
Для немонотонной функции обязательно найдётся такой набор входных переменных, что
- и
Пусть, например, и . Тогда .
В любом случае, имея немонотонную функцию и обе константы, мы можем получить инвертор.
Имеем инвертор и обе константы
В предыдущих подразделах мы перебрали все возможные варианты (см. рисунок) и пришли к выводу, что имея функции, не принадлежащие классам Т0, Т1, S и M, мы всегда можем различными способами получить инвертор и обе константы.
Имея нелинейную функцию, инвертор и константу 1, получим конъюнкцию
Нелинейная функция по определению имеет в полиноме Жегалкина хотя бы один член, содержащий конъюнкцию нескольких переменных. Пусть, например, имеется некоторая нелинейная функция
Зададимся целью построить на её основе конъюнкцию
Присвоим переменным значения 1, получим:
Очевидно, что в общем случае после такого преобразования получится функция вида
где квадратные скобки означают, что выделенный ими член может присутствовать в окончательном выражении, а может и нет.
В простейшем случае при отсутствии других членов сразу получаем конъюнкцию: :
Рассмотрим другие варианты.
- .
Любое из этих выражений, используя инвертор, можно привести к конъюнкции.
Таким образом, имея нелинейную функцию, инвертор и константу 1 всегда можно получить конъюнкцию.
Имея конъюнкцию и инвертор, получим дизъюнкцию
Имея инвертор и конъюнкцию, всегда можно получить дизъюнкцию:
- Теорема доказана.
Следствие
Функция в одиночку является полной системой тогда и только тогда, когда:
- не является самодвойственной
Примерами функций, в одиночку являющихся полной системой, будут штрих Шеффера и стрелка Пирса .
Теорема о максимальном числе функций в базисе
|
Доказательство
1) Докажем, что из любой полной системы функций можно выделить полную подсистему, состоящую не более чем из четырёх функций.
Согласно критерию Поста, в полной системе должны присутствовать пять функций:
Рассмотрим функцию . Возможны два случая:
- тогда : и система полна.
- тогда : и система полна.
2) Покажем, что существует базис из четырёх функций. Рассмотрим систему функций . Эта система полна:
Однако ни одна его подсистема не полна:
Теорема доказана.
Примечания
- Алексеев В.Б. (2002), с. 12.
Литература
- Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2000.
- Фудзисава Т., Касами Т. Математика для радиоинженеров: теория дискретных структур. — М.: Радио и связь, 1984. — 240 с.
- Алексеев В. Б. Дискретная математика (II семестр). — М., МГУ, 2002. — 44 с.
- Белоусов А. И., Ткачев С. Б. Дискретная математика. — М.: МГТУ, 2006. — 744 с. — ISBN 5-7038-2886-4.
- Гиндикин С. Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
Ссылки