Декомпозиция графа на ветви
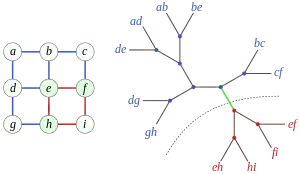
В теории графов декомпозиция на ветви неориентированного графа G — это иерархическая кластеризация рёбер графа G, представленная некорневым бинарным деревом T с рёбрами из G в качестве листьев. Удаление любого ребра из T делит рёбра графа G на два подграфа, а шириной декомпозиции считается максимальное число общих вершин в любом подграфе, полученным таким образом. Ширина ветвления графа G — это минимальная ширина любой декомпозиции графа G на ветви.
Ширина ветвления тесно связана с древесной шириной — для всех графов они находятся в пределах постоянного множителя друг от друга и обе величины могут быть описаны запрещёнными минорами. Как и для древесной ширины, многие задачи оптимизации на графах могут быть эффективно решены на графах с малой шириной ветвления. Однако, в отличие от древесной ширины, ширина ветвления планарного графа может быть вычислена точно за полиномиальное время. Декомпозиция на ветви и ширина ветвления могут быть обобщены с графов на матроиды.
Определения
Некорневое бинарное дерево — это связный неориентированный граф без циклов, в котором каждый нелистовой узел имеет в точности три соседа. Декомпозиция на ветви может быть представлена как некорневое бинарное дерево T вместе с биекцией между листьями дерева T и рёбрами заданного графа G = (V,E). Если e — любое ребро дерева T, то удаление e из T делит его на два поддерева T1 и T2. Это разделение дерева T на поддеревья порождает разделение рёбер, ассоциированных с листьями дерева T, на два подграфа графа G, G1 и G2. Такое деление графа G на два подграфа называется e-разделением.
Ширина e-разделения — это число вершин графа G, которые инцидентны как рёбрам из E1, так и рёбрам из E2. То есть это множество вершин, общих для подграфов G1 и G2. Ширина декомпозиции на ветви — это максимальная ширина любого e-разделения. Ширина ветвления графа G — это минимальная ширина декомпозиций по ветвям графа G.
Связь с шириной дерева
Декомпозиция графа на ветви тесно связана с древесной декомпозицией, а ширина ветвления тесно связана с древесной ширине. Две эти величины отличаются не более чем на постоянный множитель. В частности, в статье, в которой они предложили ширину ветвления, Нейл Робертсон и Пол Сеймур[1] показали, что для графа G с древесной шириной k и шириной ветвления b > 1
Ширина нарезки
Ширина нарезки — это концепция, определённая аналогично ширине ветвления, с той лишь разницей, что в определениях вершины и рёбра меняются местами. Декомпозиция нарезкой — это некорневое бинарное дерево, в котором каждый лист представляет вершину исходного графа, а ширина разреза — это число (или полный вес во взвешенных графах) рёбер, которые инцидентны вершине в обоих поддеревьях.
Алгоритмы определения ширины ветвления обычно работают путём сведения к эквивалентной задаче определения ширины нарезки. В частности, ширина нарезки срединного графа в точности вдвое больше ширины ветвления исходного графа[2].
Алгоритмы и сложность
Задача определения, имеет ли граф G декомпозицию на ветви с шириной, не превосходящей k, является NP-полной, если G и k являются входными данными задачи[2]. Однако графы с шириной ветвления не большей k, образуют семейство графов, замкнутое по минорам[3], откуда следует, что вычисление ширины ветвления является фиксированно-параметрически разрешимой задачей: существует алгоритм для вычисления оптимальной декомпозиции на ветви, время работы которого на графах с шириной ветвления, не превосходящей k для некоторой постоянной k, линейно зависит от размера графа[4]
Для планарных графов ширина ветвления может быть вычислена за линейное время. Это контрастирует с древесной шириной, для которой сложность вычисления на планарных графах является хорошо известной открытой проблемой[5]. Исходный алгоритм вычисления ширины ветвления для планарных графов Пола Сеймура и Робина Томаса решал задачу за время O(n2) на графе с n вершинами, а их алгоритм для построения декомпозиции на ветви работал за время O(n4)[2]. Позднее последний был улучшен до O(n3)[6].
Как и в случае древесной ширины, ширина ветвления может быть использована в качестве базиса алгоритмов динамического программирования для многих NP-трудных задач оптимизации, и в этих алгоритмах время решения будет экспоненциальным от ширины входного графа или матроида[7][8]. Например, Кук и Сеймур[9] применили основанный на ширине ветвления метод динамического программирования к задаче слияния частичных решений задачи коммивояжёра в одно глобальное решение путём формирования разреженного графа из объединения частичных решений, для чего использовалась эвристическая спектральная кластеризация для нахождения хорошей декомпозиции на ветви, после чего к полученной декомпозиции они применили динамическое программирование. Фомин и Тиликос[10] убеждают, что ширина ветвления работает лучше, чем древесная ширина, при разработке фиксированно-параметрически разрешимых алгоритмов на планарных графах по многим причинам — ширина ветвления может быть теснее ограничена функцией параметра, чем ограничение древесной ширины, она может быть вычислена за полиномиальное время и алгоритм вычисления ширины ветвления не имеет больших скрытых констант.
Обобщения для матроидов
Можно также определить понятие декомпозиции по ветвям для матроидов, что обобщает декомпозицию графов по ветвям[11]. Декомпозиция матроида по ветвям является иерархической кластеризацией элементов матроида, представленная как некорневое бинарное дерево с элементами матроида в качестве листьев. Для матроидов e-разделение можно определить тем же способом, что и для графов, а в результате получаем разделения множества M элементов матроида на два подмножества A и B. Если через ρ обозначить функцию ранга матроида, то ширина e-разделения определяется как ρ(A) + ρ(B) − ρ(M) + 1, а ширина декомпозиции и ширина ветвления матроида определяются аналогично определениям для графа. Ширина ветвления графа и ширина ветвления соответствующего графового матроида могут отличаться. Например, путь из трёх рёбер и звезда из трёх рёбер имеют разные ширины ветвления, 2 и 1 соответственно, но для них графовый матроид один и тот же, и он имеет ширину ветвления 1[12]. Однако для графов, не являющихся деревьями, ширина ветвления графа равна ширине ветвления ассоциированного графового матроида[12][13]. Ширина ветвления матроида равна ширине ветвления его двойственного матроида, и из этого в частности следует, что ширина ветвления любого планарного графа, не являющегося деревом, равна ширине ветвления его двойственного графа[12].
Ширина ветвления является важной компонентой попыток расширить теорию миноров графа на миноры матроидов — хотя древесная ширина может быть также обобщена на матроиды[14] и играет в теории миноров графов бо́льшую роль, чем ширина ветвления, ширина ветвления имеет более удобные свойства в матроидах[15]. Робертсон и Сеймур высказали предположение, что матроиды, представимые любым конкретным конечным полем, вполне квазиупорядоченны, что является аналогией теоремы Робертсона – Сеймура для графов, но гипотеза доказана только для матроидов с ограниченной шириной ветвления[16][15]. Кроме того, если семейство матроидов, замкнутое по минорам и представимое конечным полем, не включает графовые матроиды всех планарных графов, то существует постоянная, ограничивающая ширину ветвления в семействе, что обобщает соответствующее утверждение для семейств графов, замкнутых по минорам[15][17].
Для любого фиксированного k матроиды с шириной ветвления, не превосходящей k, могут быть распознаны за полиномиальное время алгоритмом, который получает доступ к матроиду через оракула независимости [18].
Запрещённые миноры
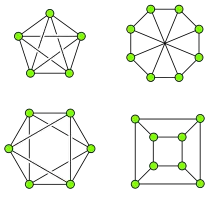
По теореме Робертсона — Сеймура графы с шириной ветвления k могут быть охарактеризованы конечным множеством запрещённых миноров. Графы с шириной ветвления 0 — это паросочетания, а минимальные запрещённые миноры в этом случае — это путь из двух дуг и треугольный граф (а также цикл из двух дуг, если рассматриваются мультиграфы)[19]. Графы с шириной ветвления 1 — это графы, в которых каждая связная компонента является звездой, а минимальные запрещённые миноры для графов с шириной ветвления 1 — это треугольный граф (или цикл из двух дуг, если рассматриваются мультиграфы) и пути из трёх дуг[19]. Графы с шириной ветвления 2 — это графы, в которых каждая двусвязная компонента является параллельно-последовательным графом, а единственным минимальным запрещённым минором является полный граф K4 из четырёх вершин[19]. Граф имеет ширину ветвления три тогда и только тогда, когда его древесная ширина равна трём и он не имеет граф гиперкуба в качестве минора. Таким образом, четыре запрещённых минора — это три из четырёх запрещённых миноров графов с древесной шириной три (граф октаэдра, полный граф K5, и граф Вагнера) вместе с графом куба[20].
Запрещённые миноры изучаются также и для ширины ветвления матроида, несмотря на отсутствие полной аналогии теоремы Робертсона — Сеймура в этом случае. Матроид имеет ширину ветвления единица тогда и только тогда, когда любой элемент является либо петлёй, либо копетлёй, так что единственным минимальным запрещённым минором является однородный матроид U(2,3), графовый матроид треугольного графа. Матроид имеет ширину ветвления два тогда и только тогда, когда он является графовым матроидом графа с шириной ветвления два, так что минимальными запрещёнными минорами являются графовые матроиды графа K4 и неграфовый матроид U(2,4). Матроиды с шириной ветвления три не вполне квазиупорядоченны без дополнительного предположения представления над конечным полем, но, тем не менее, матроиды с любой ограниченной шириной ветвления имеют конечное число минимальных запрещённых миноров, которые имеют число элементов, зависящих от ширины ветвления не более чем экспоненциально[21][22].
Примечания
- Robertson, Seymour, 1991, с. 168, Theorem 5.1.
- Seymour, Thomas, 1994.
- Robertson, Seymour, 1991, с. 164, Theorem 4.1.
- Bodlaender, Thilikos (1997). Фомин, Мацойт и Тодинка Fomin, Mazoit, Todinca (2009) описывают алгоритм с улучшенной зависимостью от k, (2√3)k, но зависимость от числа вершин увеличивается от линейного к квадратичному.
- Kao, 2008.
- Gu, Tamaki, 2008.
- Hicks, 2000.
- Hliněný, 2003.
- Cook, Seymour, 2003.
- Fomin, Thilikos, 2006.
- Robertson, Seymour, 1991, с. 188–190, Section 12, «Tangles and Matroids».
- Mazoit, Thomassé, 2007.
- Hicks, McMurray, 2007.
- Hliněný, Whittle, 2006.
- Geelen, Gerards, Whittle, 2006.
- Geelen, Gerards, Whittle, 2002.
- Geelen, Gerards, Whittle, 2007.
- Oum, Seymour, 2007.
- Robertson, Seymour, 1991, с. 165, Theorem 4.2.
- Bodlaender, Thilikos (1999). Четвёртый запрещённый минор для древесной ширины три, граф пентагональной призмы, имеет граф куба в качестве минора, так что он не является минимальным для ширины ветвления три.
- Hall, Oxley, Semple, Whittle, 2002.
- Geelen, Gerards, Robertson, Whittle, 2003.
Литература
- Hans L. Bodlaender, Dimitrios M. Thilikos. Proc. 24th International Colloquium on Automata, Languages and Programming (ICALP '97). — Springer-Verlag, 1997. — Т. 1256. — С. 627–637. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-63165-8_217.
- Hans L. Bodlaender, Dimitrios M. Thilikos. Graphs with branchwidth at most three // Journal of Algorithms. — 1999. — Т. 32, вып. 2. — С. 167—194. — doi:10.1006/jagm.1999.1011.
- William, Paul D. Seymour. Tour merging via branch-decomposition // INFORMS Journal on Computing. — 2003. — Т. 15, вып. 3. — С. 233—248. — doi:10.1287/ijoc.15.3.233.16078..
- Fedor V. Fomin, Dimitrios M. Thilikos. Dominating sets in planar graphs: branch-width and exponential speed-up. — SIAM Journal on Computing. — 2006. — Т. 36. — С. 281. — doi:10.1137/S0097539702419649.
- Fedor V. Fomin, Frédéric Mazoit, Ioan Todinca. Computing branchwidth via efficient triangulations and blocks // Discrete Applied Mathematics. — 2009. — Т. 157, вып. 12. — С. 2726—2736. — doi:10.1016/j.dam.2008.08.009..
- Jim Geelen, Bert Gerards, Neil Robertson, Geoff Whittle. On the excluded minors for the matroids of branch-width k // Journal of Combinatorial Theory, Series B. — 2003. — Т. 88, вып. 2. — С. 261—265. — doi:10.1016/S0095-8956(02)00046-1.
- Jim Geelen, Bert Gerards, Geoff Whittle. Branch-width and well-quasi-ordering in matroids and graphs // Journal of Combinatorial Theory, Series B. — 2002. — Т. 84, вып. 2. — С. 270—290. — doi:10.1006/jctb.2001.2082.
- Jim Geelen, Bert Gerards, Geoff Whittle. Proc. International Congress of Mathematicians. — 2006. — Т. III. — С. 827–842.
- Jim Geelen, Bert Gerards, Geoff Whittle. Excluding a planar graph from GF(q)-representable matroids // Journal of Combinatorial Theory, Series B. — 2007. — Т. 97, вып. 6. — С. 971—998. — doi:10.1016/j.jctb.2007.02.005..
- Qian-Ping Gu, Hisao Tamaki. Optimal branch-decomposition of planar graphs in O(n3) time // ACM Transactions on Algorithms. — 2008. — Т. 4, вып. 3. — С. 30:1—30:13. — doi:10.1145/1367064.1367070.
- Rhiannon Hall, James Oxley, Charles Semple, Geoff Whittle. On matroids of branch-width three // Journal of Combinatorial Theory, Series B. — 2002. — Т. 86, вып. 1. — С. 148—171. — doi:10.1006/jctb.2002.2120.
- Illya V. Hicks. Branch Decompositions and their Applications. — Rice University, 2000. — (Ph.D. thesis).
- Illya V. Hicks, Nolan B. McMurray, Jr. The branchwidth of graphs and their cycle matroids // Journal of Combinatorial Theory, Series B. — 2007. — Т. 97, вып. 5. — С. 681—692. — doi:10.1016/j.jctb.2006.12.007..
- Petr Hliněný. Proc. 28th International Symposium on Mathematical Foundations of Computer Science (MFCS '03). — Springer-Verlag, 2003. — Т. 2747. — С. 470–479. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-540-45138-9\_41.
- Petr Hliněný, Geoff Whittle. Matroid tree-width // European Journal of Combinatorics. — 2006. — Т. 27, вып. 7. — С. 1117—1128. — doi:10.1016/j.ejc.2006.06.005.
- Добавления и исправления: Petr Hliněný, Geoff Whittle. Addendum to matroid tree-width // European Journal of Combinatorics. — 2009. — Т. 30, вып. 4. — С. 1036—1044. — doi:10.1016/j.ejc.2008.09.028.
- Frédéric Mazoit, Stéphan Thomassé. Surveys in Combinatorics 2007 / Anthony Hilton, John Talbot. — Cambridge University Press, 2007. — Т. 346. — С. 275. — (London Mathematical Society Lecture Note Series).
- Sang-il Oum, Paul Seymour. Testing branch-width // Journal of Combinatorial Theory. — 2007. — Т. 97, вып. 3. — С. 385—393. — doi:10.1016/j.jctb.2006.06.006.
- Neil Robertson, Paul D. Seymour. Graph minors. X. Obstructions to tree-decomposition // Journal of Combinatorial Theory. — 1991. — Т. 52, вып. 2. — С. 153—190. — doi:10.1016/0095-8956(91)90061-N.
- Paul D. Seymour. Call routing and the ratcatcher // Combinatorica. — 1994. — Т. 14, вып. 2. — С. 217—241. — doi:10.1007/BF01215352.
- Encyclopedia of Algorithms / ed. Ming-Yang Kao. — Springer, 2008. — С. 969. — ISBN 9780387307701. Ещё одна давняя открытая проблема: Существует ли алгоритм полиномиального времени вычисления древесной ширины планарного графа