Некорневое двоичное дерево

Некорневое двоичное дерево — это некорневое дерево, в котором каждая вершина имеет либо одного, либо трёх соседей.

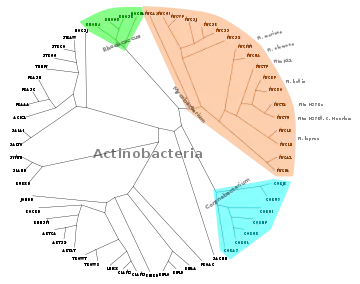
Кладограмма в виде некорневого двоичного дерева, представляющая подобие и эволюционную историю родов актинобактерий.

Определения

Свободное дерево или некорневое дерево — это связный неориентированный граф без циклов. Вершины, имеющие одного соседа, называются листьями дерева, остальные вершины называются внутренними узлами. Степень вершины — это число её соседей. В дереве с более чем одной дугой листья имеют степень единица. Неориентированное двоичное дерево — это свободное дерево, в котором все внутренние узлы имеют степень три.

В некоторых приложениях имеет смысл различать подвиды некорневых двоичных деревьев — планарное вложение дерева может быть зафиксировано путём указания циклического порядка рёбер в каждой вершине, переводя дерево в плоское дерево. В информатике двоичные деревья часто являются корневыми ориентированными деревьями, если они используются как структуры данных, но при применении некорневых двоичных деревьев в иерархической кластеризации и реконструкции эволюционных деревьев более распространены неориентированные деревья[1].

Кроме того, можно различать деревья, в которых все вершины имеют различные метки, деревья, в которых помечены только листья, и деревья, в которых узлы не помечены. Некорневое двоичное дерево с n листьями имеет n − 2 внутренних узлов, так что метки можно взять из интервала от 1 до 2n − 1, если нужно пометить все узлы, или набора чисел от 1 до n, если нужно пометить только листья[1].

Связанные структуры

Корневые двоичные деревья
Основная статья: Двоичное дерево

Некорневое двоичное дерево T может быть преобразовано в корневое двоичное дерево (то есть корневое дерево, в котором каждый нелистовой узел имеет в точности два потомка) путём выбора корневого ребра e дерева T, помещением нового корня в середине ребра e и направлением всех рёбер полученного подразделённого дерева от корня. Обратно — любое корневое дерево может быть преобразовано в некорневое двоичное дерево путём удаления корневой дуги, заменой пути между двумя его потомками одним неориентированным ребром и удалением направлений дуг в графе. По этой причине имеется в точности в 2n −3 раза больше корневых деревьев с n листьями по сравнению с некорневыми двоичными деревьями с n листьями[1].

Иерархическая кластеризация

Иерархическую кластеризациию набора объектов можно формализовать как максимальное семейство множеств объектов, в котором никакого два множества не пересекаются (но некоторые множества могут содержаться в других). То есть для двух множеств S и T в семействе либо S и T не пересекаются, либо одно множество содержится в другом, и ни одно множество не может быть добавлено в семейство с сохранением этого свойства. Если T является некорневым двоичным деревом, оно определяет иерархическую кластеризацию листьев этого дерева — для каждого ребра (u,v) из T существует кластер, состоящий из листьев, которые более близки к u, чем к v, и эти множества вместе с пустым множеством и множеством всех листьев образуют максимальное непересекающееся семейство. В обратную сторону, из любого семейства непересекающихся множеств над множеством из n элементов можно сформировать единственное некорневое двоичное дерево, которое имеет узел для любой тройки (A,B,C) непересекающихся множеств из семейства, покрывающих вместе все элементы [2].

Эволюционные деревья

Согласно простым видам теории эволюции, историю жизни можно свести в филогенетическое дерево, в котором каждый узел описывает род, листья представляют существующие ныне виды, а рёбра представляют связь родитель-потомок между родами. Это дерево имеет естественную ориентацию рёбер от родительского вида к потомкам, а корень является общим предком видов, так что такое дерево является корневым деревом. Однако некоторые методы восстановления двоичных деревьев могут восстановить только узлы и рёбра этого дерева, но не их ориентацию.

Например, методы кладистики, такие как принципы наибольшей экономии, используют в качестве данных множество двоичных свойств, описывающих признаки этих родов. Эти методы ищут дерево с заданными видами в качестве листьев, в котором внутренние узлы также помечены некоторыми признаками, и пытаются минимизировать число случаев, в которых признак присутствует только на одной вершине ребра в дереве. Идеально — каждый признак может иметь только одно ребро с таким случаем. Изменение корня дерева не изменяет число рёбер с различными признаками, так что методы, основанные на принципах наибольшей экономии, не имеют возможности определить положение корня дерева и создают некорневое дерево, зачастую некорневое двоичное дерево[3].

Некорневые двоичные деревья можно также образовать методами реконструкции эволюционных деревьев, основанными на определении данных для каждых четырёх родов листьев, некорневого двоичного дерева, описывающего эволюцию этих четырёх видов, и методами, которые используют тетрадное расстояние для измерения расстояния между деревьями[4].

Декомпозиция на ветви

Некорневые двоичные деревья используются также для определения декомпозиции графа на ветви графов путём образования некорневого двоичного дерева, листья которого представляют рёбра данного графа. То есть, декомпозицию графа на ветви можно рассматривать как иерархическую кластеризацию рёбер грфа. Декомпозиция графа на ветви и соответствующая численная величина, ширина ветвления, тесно связаны с древесной шириной и образуют основу для построения эффективных алгоритмов динамического программирования на графах[5].

Перечисление

Ввиду применения некорневых двоичных деревьев в иерархической кластеризации, наиболее естественной задачей перечисления графов на некорневых двоичных деревьях является подсчёт числа деревьев с n помеченными листьями и непомеченными внутренними узлами. Некорневое двоичное дерево с n помеченными листьями может быть образовано путём соединения n-го листа с новым узлом в середине любого ребра некорневого двоичного дерева с n − 1 помеченными листьями. Имеется 2n − 5 рёбер, к которым n-ый узел можно добавить. Таким образом, число деревьев с n листьями больше, чем число деревьев с n − 1 листьями в 2n − 5 раз, так что число деревьев с n помеченными листьями равно двойному факториалу

[6].

Число деревьев с 2, 3, 4, 5, ... помеченными листьями равно

1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, ... (последовательность A001147 в OEIS).

Альтернативные названия

Некорневые двоичные деревья также называются свободными двоичными деревьями[7], кубическими деревьями[8], тернарными деревьями[5] и некорневыми тернарными деревьями[9]. Однако, название «свободное двоичное дерево» также используется для некорневых деревьев, которые могут иметь узлы степени два[10] и для корневых бинарных деревьев с неориентированными потомками[11], а название «троичное дерево» чаще используется в смысле «корневое дерево с тремя потомками».

Примечания
  1. Furnas, 1984.
  2. См., например, статью Эпштейна (Eppstein 2009) о соответствии между кластеризациями и деревьями, но в статье используются корневые двоичные деревья, а не некорневых деревьев, а потому включают произвольный выбор корневого узла.
  3. Hendy, Penny, 1989.
  4. St. John, Warnow, Moret, Vawterd, 2003.
  5. Robertson, Seymour, 1991.
  6. Balding, Bishop, Cannings, 2007.
  7. Czumaj, Gibbons, 1996.
  8. Exoo, 1996.
  9. Cilibrasi, Vitanyi, 2006.
  10. Harary, Palmer, Robinson, 1992.
  11. Przytycka, Larmore, 1994.

Литература
  • D. J. Balding, Martin J. Bishop, Christopher Cannings. Handbook of Statistical Genetics. — 3rd. — Wiley-Interscience, 2007. — Т. 1. — С. 502. — ISBN 978-0-470-05830-5.
  • Rudi Cilibrasi, Paul M.B. Vitanyi. A new quartet tree heuristic for hierarchical clustering. — 2006.
  • Artur Czumaj, Alan Gibbons. Guthrie's problem: new equivalences and rapid reductions // Theoretical Computer Science. — 1996. — Т. 154, вып. 1. — С. 3–22. — doi:10.1016/0304-3975(95)00126-3.
  • David Eppstein. Squarepants in a tree: Sum of subtree clustering and hyperbolic pants decomposition // ACM Transactions on Algorithms. — 2009. — Т. 5, вып. 3. — С. 1–24. — doi:10.1145/1541885.1541890. — arXiv:cs.CG/0604034.
  • Geoffrey Exoo. A simple method for constructing small cubic graphs of girths 14, 15, and 16 // Electronic Journal of Combinatorics. — 1996. — Т. 3, вып. 1.
  • George W. Furnas. The generation of random, binary unordered trees // Journal of Classification. — 1984. — Т. 1, вып. 1. — С. 187–233. — doi:10.1007/BF01890123.
  • Frank Harary, E.M. Palmer, R.W. Robinson. Counting free binary trees admitting a given height // Journal of Combinatorics, Information, and System Sciences. — 1992. — Т. 17. — С. 175–181.
  • Michael D. Hendy, David Penny. A framework for the quantitative study of evolutionary trees // Systematic Biology. — 1989. — Т. 38, вып. 4. — С. 297–309. — doi:10.2307/2992396. — .
  • Teresa M. Przytycka, Lawrence L. Larmore. The optimal alphabetic tree problem revisited // Proc. 21st International Colloquium on Automata, Languages and Programming (ICALP '94). — Springer-Verlag, 1994. — Т. 820. — С. 251–262. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-58201-0_73.
  • Neil Robertson, Paul D. Seymour. Graph minors. X. Obstructions to tree-decomposition // Journal of Combinatorial Theory. — 1991. — Т. 52, вып. 2. — С. 153–190. — doi:10.1016/0095-8956(91)90061-N.
  • Katherine St. John, Tandy Warnow, Bernard M. E. Moret, Lisa Vawterd. Performance study of phylogenetic methods: (unweighted) quartet methods and neighbor-joining // Journal of Algorithms. — 2003. — Т. 48, вып. 1. — С. 173–193. — doi:10.1016/S0196-6774(03)00049-X.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.