Спектральная кластеризация
Техники спектральной кластеризации используют спектр (собственные значения) матрицы сходства данных для осуществления снижения размерности перед кластеризацией в пространствах меньших размерностей. Матрица сходства подаётся в качестве входа и состоит из количественных оценок относительной схожести каждой пары точек в данных.
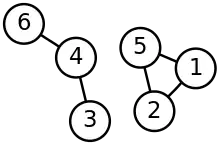
В приложении к сегментации изображений спектральная кластеризация известна как кластеризация объектов на основе сегментации.
Алгоритмы
Если задано пронумерованное множество точек данных, матрицу сходства можно определить как симметричную матрицу , в которой элементы представляют меру схожести между точками данных с индексами и . Общий принцип спектральной кластеризации — использование стандартного метода кластеризации (существует много таких методов, метод k-средних обсуждается ниже) на значимых собственных векторах матрицы Кирхгофа матрицы . Существует много различных способов определения матрицы Кирхгофа, которая имеет различные математические интерпретации, так что кластеризация будет также иметь различные интерпретации. Значимые собственные вектора — это те, которые соответствуют наименьшим нескольким собственным значениям матрицы Кирхгофа, за исключением собственных значений 0. Для обеспечения вычислительной эффективности эти собственные вектора часто вычисляются как собственные вектора, соответствующие некоторым наибольшим собственным значениям функции от матрицы Кирхгофа.
Одна из техник спектральной кластеризации — алгоритм нормализованных сечений (или алгоритм Ши — Малика), предложенный Джиамбо Ши и Джитендра Маликом[1], широко используемый метод для сегментации изображений. Алгоритм разбивает точки на два множества основываясь на собственном векторе , соответствующем второму по величине собственному значению симметрично нормализованной матрицы Кирхгофа, задаваемой формулой
где — диагональная матрица
Математически эквивалентный алгоритм[2] использует собственный вектор, соответствующий наибольшему собственному значению нормализованной матрицы Кирхгофа случайного блуждания . Алгоритм Мейла – Ши был проверен в контексте диффузионных карт, которые, как обнаружилось, имеют связь с вычислительной квантовой механикой[3].
Другая возможность — использование матрицы Кирхгофа, задаваемой выражением
а не симметрично нормализованной матрицы Кирхгофа.
Разбиение можно осуществить различными способами, такими как вычисление медианы компонент второго наименьшего собственного вектора и помещение всех точек в , компоненты которых в больше, чем , остальные точки помещаются в . Алгоритм можно использовать для иерархической кластеризации путём последовательного разбиения подмножеств подобным способом.
Если алгебраически матрица сходства ещё не построена, эффективность спектральной кластеризации может быть улучшена, если решение соответствующей задачи — поиск собственных значений осуществить безматричным методом (без явного манипулирования или даже вычисления матрицы сходства), таким как алгоритм Ланцоша.
Для графов большого размера второе собственное значение (нормализованной) матрицы Кирхгофа графа часто плохо обусловлено, что приводит к медленной сходимости итеративных методов поиска собственных значений. Предобуславливание является ключевой техникой улучшения сходимости, для примера, в безматричном методе LOBPCG. Спектральная кластеризация была успешно применена к большим графам первым делом путём распознавания структуры сетевого сообщества, а затем уж кластеризации сообщества[4].
Спектральная кластеризация тесно связана с нелинейным понижением размерности и могут быть использованы техники понижения размерности, такие как локально линейное вложение, для уменьшения погрешности от шума или выброса в наблюдениях[5].
Бесплатное программное обеспечение для имплементации спектральной кластеризации доступно в больших проектах с открытым исходным кодом, таких как Scikit-learn[6], MLlib для кластеризации на основе псевдособственных значений с использованием метода степенной итерации[7], языка R[8].
Связь с k-средними
Задача о k-средних с нелинейным ядром является расширением задачи о k-средних, в которой входные точки отображаются нелинейно в пространство признаков высокой размерности с помощью ядерной функции . Взвешенная задача о k-средних с нелинейным ядром расширяет задачу далее, задавая вес для каждого кластера как значение, обратно пропорциональное числу элементов кластера,
Пусть — матрица нормализованных коэффициентов для каждой точки любого кластера, в которой , если , и 0 в противном случае. Пусть — матрица ядра для всех точек. Взвешенная задача о k-средних с нелинейным ядром с n точками и k кластерами задаётся как задача максимизации
при условиях
При этом . Кроме того, задано ограничение на коэффициенты
- ,
где представляет собой вектор из единиц.
Задачу можно преобразовать в
Эта задача эквивалентна задаче спектральной кластеризации, когда ограничение на ослаблено. В частности, взвешенная задача k-средних с нелинейным ядром может быть переформулирована как задача спектральной кластеризации (разбиения графа), и наоборот. Выходом алгоритма служат собственные вектора, которые не удовлетворяют ограничениям на индикаторные переменные, определённые вектором . Следовательно, требуется постобработка собственных векторов, чтобы задачи были эквивалентными[9]. Преобразование задачи спектральной кластеризации во взвешенную задачу о k-средних с нелинейным ядром существенно сокращает вычислительные затраты[10].
Меры для сравнения кластеризации
Рави Каннан, Сантош Вемпала и Адриан Ветта[11] предложили бикритериальную меру для определения качества кластеризации. Они говорят, что кластеризация является (α, ε)-кластеризацией, если проводимость каждого кластера не меньше α, а вес межкластерных рёбер не превышает ε доли от веса всех рёбер в графе. В той же статье они рассматривают также два аппроксимационных алгоритма.
См. также
- Метод распространения близости
- Ядерный метод главных компонент
- Кластерный анализ
- Спектральная теория графов
Примечания
- Shi, Malik, 2000.
- Meilă, Shi, 2001, с. 873–879.
- Scott, Therani, Wang, 2017, с. 1-17.
- Zare, Shooshtari, Gupta, Brinkman, 2010, с. 403.
- Arias-Castro, Chen, Lerman, 2011, с. 1537–1587.
- 2.3. Clustering — scikit-learn 0.20.2 documentation
- Clustering - RDD-based API - Spark 2.4.0 Documentation
- CRAN - Package kernlab
- Dhillon, Guan, Kulis, 2004, с. 551–556.
- Dhillon, Guan, Kulis, 2007, с. 1-14.
- Kannan, Vempala, Vetta, 2000, с. 497–515.
Литература
- Marina Meilă, Jianbo Shi. Learning Segmentation by Random Walks // Neural Information Processing Systems. — 2001. — Т. 13 (NIPS 2000). Архивная копия от 10 декабря 2015 на Wayback Machine
- Jianbo Shi, Jitendra Malik. Normalized Cuts and Image Segmentation // IEEE Transactions on PAMI. — 2000. — Август (т. 22, вып. 8).
- T.C. Scott, Madhusudan Therani, Xing M. Wang. Data Clustering with Quantum Mechanics // Mathematics. — 2017. — Т. 5, вып. 1. — С. 1–17. — doi:10.3390/math5010005.
- Habil Zare, P. Shooshtari, A. Gupta, R. Brinkman. Data reduction for spectral clustering to analyze high throughput flow cytometry data // BMC Bioinformatics. — 2010. — Т. 11. — С. 403. — doi:10.1186/1471-2105-11-403. — PMID 20667133.
- E. Arias-Castro, G. Chen, G. Lerman. Spectral clustering based on local linear approximations. // Electronic Journal of Statistics. — 2011. — Т. 5. — С. 1537–1587. — doi:10.1214/11-ejs651.
- I.S. Dhillon, Y. Guan, B. Kulis. Kernel k-means: spectral clustering and normalized cuts // Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining. — 2004. — С. 551–556.
- Inderjit Dhillon, Yuqiang Guan, Brian Kulis. Weighted Graph Cuts without Eigenvectors: A Multilevel Approach // IEEE Transactions on Pattern Analysis and Machine Intelligence. — 2007. — Ноябрь (т. 29, вып. 11). — doi:10.1109/tpami.2007.1115.
- Ravi Kannan, Santosh Vempala, Adrian Vetta. On Clusterings : Good. Bad and Spectral // Journal of the ACM. — 2000. — Т. 51. — doi:10.1145/990308.990313.