Группа Вейля

Группа Вейля — группа, порождённая отражениями в гиперплоскостях, ортогональных к корням корневой системы группы Ли, алгебры Ли или других алгебраических объектов.

Названа в честь Германа Вейля.

Связанные определения

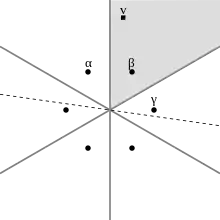
Шесть камер Вейля корневой системы A₂.

Гиперплоскости, ортогональные корням корневой системы, режут Евклидово пространство на конечное число открытых областей, называемых камерами Вейля.
Для группы Ли $G$ , удовлетворяющей определенным условиям (например, для связной компактной группы), и произвольного тора $T<G$ (не обязательно максимального) можно определить группу Вейля как фактор нормализатора тора $N(T)$ по его централизатору $Z(T)$ ,
$W(T,G)=N(T)/Z(T).$

Группа

W(T,G)

конечна, поскольку '

Z(T)

имеет конечный индекс в

N(T)

.

При этом, если $T=T_{0}$ — максимальный тор (и значит $Z(T_{0})=T_{0}$ ), то полученная факторгруппа $W(T_{0},G)=N(T_{0})/Z(T_{0})$ называется группой Вейля $G$ , и обозначается $W(G)$ .

Хотя эта конструкция зависит от выбора максимального тора, все полученные таким образом группы изоморфны.
Если $G$ - компактная и связная группа Ли, то её группа Вейля изоморфна группе Вейля её алгебры Ли.

Группа Вейля действует перестановками на камерах Вейля, это действие свободное и транзитивное.
- В частности, число камер Вейля равно порядку группы Вейля.

Группы Вейля являются конечными группами Коксетера. Это позволяет им быть классифицированными диаграммами Кокстера — Дынкина.

Группа Вейля алгебры Ли ${\mathfrak {sl}}_{n}$ является симметрической группой на n элементах, $S_{n}$ . Её действие можно описать следующим образом. Если ${\mathfrak {h}}$ — подалгебра Картана всех диагональных матриц с нулевым следом, то $S_{n}$ действует на ${\mathfrak {h}}$ перестановкой диагональных элементов перестановки матриц. Это действие индуцирует действие на двойственном пространстве ${\mathfrak {h}}^{\ast }$ , которое собственно и является действием группы Вейля.

Для общей линейной группы GL максимальный тор образован подгруппой D обратимых диагональных матриц. Нормализатор подгруппы D является группой обобщенных матриц перестановок (матриц типа матриц перестановок, но с любыми ненулевыми числами, вместо единиц). Группа Вейля является симметрической группой. В этом случае отображение N → N/T расщепляется, поэтому нормализатор N является полупрямым произведением тора и группы Вейля и значит группа Вейля может быть идентифицирована с подгруппе G.
- В общем это не всегда так – частное не всегда расщепляется, нормализатор N не всегда полупрямое произведение и группа Вейля не всегда реализуется как подгруппа G.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.