Граф МакГи
В теории графов графом МакГи, или (3-7)-клеткой, называется 3-регулярный граф с 24 вершинами и 36 рёбрами.[1]
| Граф МакГи | |
|---|---|
 | |
| Назван в честь | W. F. McGee |
| Вершин | 24 |
| Рёбер | 36 |
| Радиус | 4 |
| Диаметр | 4 |
| Обхват | 7 |
| Автоморфизмы | 32 |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Свойства |
кубический клетка гамильтонов |
Граф МакГи — это единственная (3,7)-клетка (наименьший кубический с обхватом 7). Он является наименьшей кубической клеткой, не являющейся графом Мура.
Впервые открытый Хорстом Саксом, но не опубликованный[2], граф назван в честь МакГи (W. F. McGee), который опубликовал результат в 1960 году[3]. Позднее, в 1966 году, Уильям Томас Татт доказал, что это единственная (3,7)-клетка[4][5][6].
Известны наименьшие кубические графы с числом скрещиваний 1—8 (последовательность A110507 в OEIS), наименьший граф с числом скрещиваний 8 — это граф МакГи. Существует 5 неизоморфных кубических графов порядка 24 с числом скрещиваний 8[7], один из них — обобщённый граф Петерсена G(12,5), известный также как Граф Науру[8].
Граф МакГи имеет радиус 4, диаметр 4, хроматическое число 3 и хроматический индекс 3. Он также 3-вершинно-связен и 3-рёберно-связен.
Алгебраические свойства
Характеристический многочлен графа МакГи равен .
Автоморфизм группы графа МакГи имеет порядок 32 и не транзитивен относительно вершин — имеется две орбиты вершин длины 8 и 16. Граф МакГи — это наименьшая кубическая клетка, не являющаяся вершинно-транзитивной[9].
Галерея
 Число пересечений графа МакГи равно 8.
Число пересечений графа МакГи равно 8.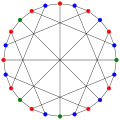 Хроматическое число графа МакГи равно 3.
Хроматическое число графа МакГи равно 3.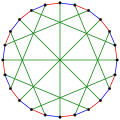 Хроматический индекс графа МакГи ракен 3.
Хроматический индекс графа МакГи ракен 3.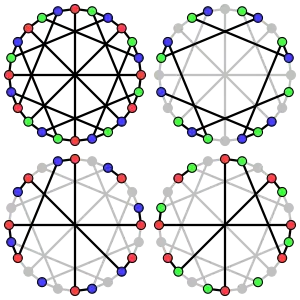 The Ациклический хроматический индекс графа МакГи равен 3.
The Ациклический хроматический индекс графа МакГи равен 3.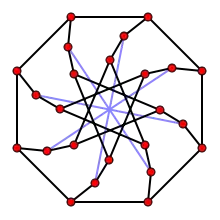 Альтернативное изображение графа МакГи.
Альтернативное изображение графа МакГи.
Примечания
- Weisstein, Eric W. McGee Graph (англ.) на сайте Wolfram MathWorld.
- Kárteszi, F. «Piani finit ciclici come risoluzioni di un certo problemo di minimo.» Boll. Un. Mat. Ital. 15, 522—528, 1960
- McGee, W. F. «A Minimal Cubic Graph of Girth Seven.» Canad. Math. Bull. 3, 149—152, 1960
- Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
- Wong, P. K. «Cages--A Survey.» J. Graph Th. 6, 1-22, 1982
- Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
- Pegg, E. T. and Exoo, G. «Crossing Number Graphs.» Mathematica J. 11, 2009
- Weisstein, Eric W. Graph Crossing Number (англ.) на сайте Wolfram MathWorld.
- Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
