Граф Мура

Граф Петерсена как граф Мура. Любое дерево поиска в ширину имеет ${\displaystyle d(d-1)^{i}}$ вершин в его i-ом уровне.

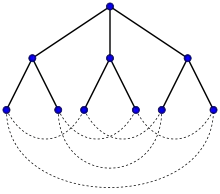
Пусть ${\displaystyle G}$ — любой граф с максимальной степенью ${\displaystyle d}$ и диаметром ${\displaystyle k}$, тогда возьмём дерево, образованное поиском в ширину, с корнем в вершине ${\displaystyle v}$. Это дерево имеет 1 вершину уровня 0 (сама вершина ${\displaystyle v}$), и максимум ${\displaystyle d}$ вершин уровня 1 (соседи вершины ${\displaystyle v}$). На следующем уровне имеется максимум ${\displaystyle d(d-1)}$ вершин — каждый сосед вершины ${\displaystyle v}$ использует одно ребро для соединения с вершиной ${\displaystyle v}$, так что имеет максимум ${\displaystyle d-1}$ соседей уровня 2. В общем случае подобные доводы показывают, что на любом уровне ${\displaystyle 1\leq {i}\leq {k}}$ может быть не больше ${\displaystyle d(d-1)^{i}}$ вершин. Таким образом, общее число вершин может быть не больше

${\displaystyle 1+d\sum _{i=0}^{k-1}(d-1)^{i}.}$

Хоффман и Синглтон[2] первоначально определили граф Мура как граф, для которого эта граница числа вершин достигается. Таким образом, любой граф Мура имеет максимально возможное число вершин среди всех графов, в которых степень не превосходит ${\displaystyle d}$, диаметр — ${\displaystyle k}$.

Позднее Синглтон[4] показал, что графы Мура можно эквивалентно определить как граф, имеющий диаметр ${\displaystyle k}$ и обхват ${\displaystyle 2k-1}$. Эти два требования комбинируются, из чего выводится d-регулярность графа для некоторого ${\displaystyle d}$.

Вместо верхней границы числа вершин в графе в терминах его максимальной степени и диаметра мы можем использовать нижнюю границу числа вершин в терминах минимальной степени и обхвата [3]. Предположим, что граф ${\displaystyle G}$ имеет минимальную степень ${\displaystyle d}$ и обхват ${\displaystyle 2k+1}$. Выберем произвольную начальную вершину ${\displaystyle v}$ и, как и прежде, представим дерево поиска в ширину с корнем в ${\displaystyle v}$. Это дерево должно иметь одну вершину уровня 0 (сама вершина ${\displaystyle v}$) и по меньшей мере ${\displaystyle d}$ вершин на уровне 1. На уровне 2 (для ${\displaystyle k>1}$), должно быть по меньшей мере ${\displaystyle d(d-1)}$ вершин, поскольку каждая вершина на уровне ${\displaystyle l}$ имеет по меньшей мере ${\displaystyle d-1}$ оставшихся связей, и никакие две вершины уровня 1 не могут быть смежными или иметь общие вершины уровня 2, поскольку создался бы цикл, более короткий, чем обхват. В общем случае похожие доводы показывают, что на любом уровне ${\displaystyle 1\leq {i}\leq {k}}$ должно быть по меньшей мере ${\displaystyle d(d-1)^{i}}$ вершин. Таким образом, общее число вершин должно быть не менее

${\displaystyle 1+d\sum _{i=0}^{k-1}(d-1)^{i}.}$

В графе Мура это число вершин достигается. Каждый граф Мура имеет обхват в точности ${\displaystyle 2k+1}$ — он не имеет достаточно вершин, чтобы иметь больший обхват, а более короткий цикл привёл бы к недостатку вершин в первых ${\displaystyle k}$ уровнях некоторых деревьев поиска в ширину. Таким образом, любой граф Мура имеет минимально возможное число вершин среди всех графов с минимальной степенью ${\displaystyle d}$ и диаметром ${\displaystyle k}$ — он является клеткой.

Для чётного обхвата ${\displaystyle 2k}$ можно образовать аналогичное дерево поиска в ширину, начиная с середины одного ребра. Получаем границу минимального числа вершин в графе этого обхвата с минимальной степенью ${\displaystyle d}$

${\displaystyle 2\sum _{i=0}^{k-1}(d-1)^{i}=1+(d-1)^{k-1}+d\sum _{i=0}^{k-2}(d-1)^{i}.}$

Таким образом, в графы Мура иногда включаются графы, на которых данная граница достигается. Снова любой такой граф является клеткой.

Теорема Хоффмана — Синглтона утверждает, что любой граф Мура с обхватом 5 должен иметь степень 2, 3, 7 или 57. Графами Мура являются:

• Полные графы ${\displaystyle K_{n}}$ с n > 2 вершинами. (диаметр 1, обхват 3, степень n-1, порядок ${\displaystyle n}$)
• Нечётные циклы ${\displaystyle C_{2n+1}}$. (диаметр ${\displaystyle n}$, обхват ${\displaystyle 2n+1}$, степень 2, порядок 2n+1)
• Граф Петерсена. (диаметр 2, обхват 5, степень 3, порядок 10)
• Граф Хоффмана — Синглтона. (диаметр 2, обхват 5, степень 7, порядок 50)
• Гипотетический граф с диаметром 2, обхватом 5, степенью 57 и порядком 3250, в настоящее время неизвестно, существует ли такой.

Хигман показал, что, в отличие от других графов Мура, неизвестный граф не может быть вершинно-транзитивным. Мачай и Ширан позднее показали, что порядок автоморфизмов такого графа не превосходит 375.

В обобщённом определении графов Мура, где разрешается чётный обхват, графы с чётным обхватом соответствуют графам инцидентности (возможно вырожденных) обобщённых многоугольников. Несколько примеров — чётные циклы ${\displaystyle C_{2n}}$, полные двудольные графы ${\displaystyle K_{n,n}}$ с обхватом четыре, граф Хивуда со степенью 3 и обхватом 6 и граф Татта — Коксетера со степенью 3 и обхватом 8. Известно[5][6]), что все графы Мура, кроме перечисленных выше, должны иметь обхват 5, 6, 8 или 12. Случай чётного обхвата следует из теоремы Фейта-Хигмана о возможных значениях ${\displaystyle n}$ для обобщённых n-угольников.

• Проблема размера — диаметра
• Таблица наибольших известных графов для заданного диаметра и максимальной степени

• Jernej Azarija, Sandi Klavžar. Moore Graphs and Cycles Are Extremal Graphs for Convex Cycles // Journal of Graph Theory. — 2015. — Т. 80. — С. 34–42. — doi:10.1002/jgt.21837.
• Béla Bollobás. Modern graph theory. — Springer-Verlag, 1998. — Т. 184. — (Graduate Texts in Mathematics)..
• E. Bannai, T. Ito. On finite Moore graphs // Journal of the Faculty of Science, the University of Tokyo. Sect. 1 A, Mathematics. — 1973. — Т. 20. — С. 191–208. Архивировано 24 апреля 2012 года.
• R. M. Damerell. On Moore graphs // Mathematical Proceedings of the Cambridge Philosophical Society. — 1973. — Т. 74. — С. 227–236. — doi:10.1017/S0305004100048015.
• Paul Erdős, Alfréd Rényi, Vera T. Sós. On a problem of graph theory // Studia Sci. Math. Hungar.. — 1966. — Т. 1. — С. 215–235..
• Alan J. Hoffman, Robert R. Singleton. Moore graphs with diameter 2 and 3 // IBM Journal of Research and Development. — 1960. — Т. 5, вып. 4. — С. 497–504. — doi:10.1147/rd.45.0497.
• Martin Mačaj, Jozef Širáň. Search for properties of the missing Moore graph // Linear Algebra and its Applications. — 2010. — Т. 432. — С. 2381–2398. — doi:10.1016/j.laa.2009.07.018..
• Robert R. Singleton. There is no irregular Moore graph // American Mathematical Monthly. — 1968. — Т. 75, вып. 1. — С. 42–43. — doi:10.2307/2315106.

• Brouwer and Haemers: Spectra of graphs
• Weisstein, Eric W. Moore Graph (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Hoffman-Singleton Theorem (англ.) на сайте Wolfram MathWorld.