Граф Татта — Коксетера
Граф Татта — Коксетера (также 8-клетка Татта) — 3-регулярный граф с 30 вершинами и 45 рёбрами. Единственный наименьший кубический граф с обхватом 8, является клеткой и графом Мура. Двудольный и может быть построен как граф Леви обобщённого четырёхугольника W2 (известного как конфигурация Кремоны — Ричмонда). Назван в честь Уильяма Томаса Татта и Гарольда Коксетера. Найден Уильямом Таттом (Tutte 1947), но его связь с геометрической комбинацией исследована обоими авторами в паре совместных статей (Tutte, 1958, Coxeter (a), 1958).
| Граф Татта — Коксетера | |
|---|---|
 | |
| Назван в честь |
Уильям Татт Гарольд Коксетер |
| Вершин | 30 |
| Рёбер | 45 |
| Диаметр | 4 |
| Обхват | 8 |
| Автоморфизмы | 1440 (Aut(S6)) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Свойства |
кубический
дистанционно-транзитивный |
Является одним из тринадцати кубических дистанционно-регулярных графов[1].
Двойки, наборы и автоморфизмы
Особенно простое комбинаторное построение графа Татта — Коксетера предложено Коксетером (Coxeter (b) 1958) и основывается на ранних работах Д. Д. Сильвестра (Sylvester 1844): образуем множество из шести элементов (например, это буквы a, b, c, d, e, f); Сильвестр определил двойки как 15 неупорядоченных пар элементов: ab, ac, ad, ae, af, bc, bd, be, bf, cd, ce, cf, de, df, or ef. Он также определил наборы — разбиения элементов на три двойки: (ab, cd, ef); (ab, ce, df); (ab, cf, de); (ac, bd, ef); (ac, be, df); (ac, bf, de); (ad, bc, ef); (ad, be, cf); (ad, bf, ce); (ae, bc, df); (ae, bd, cf); (ae, bf, cd); (af, bc, de); (af, bd, ce); (af, be, cd). Каждый набор содержит 3 двойки, и каждая двойка принадлежит трём наборам. Граф Татта — Коксетера можно рассматривать как граф, в котором каждая вершина соответствует двойке, а также набору двоек — по вершине для каждого набора, и рёбра соединяют каждый набор с тремя двойками, содержащихся в нём.
Основываясь на этом построении, Коксетер показал, что граф Татта — Коксетера является симметричным. Он имеет 1440 автоморфизмов графа, которые можно отождествить с автоморфизмами группы перестановок шести элементов (Coxeter (b) 1958). Внутренние автоморфизмы этой группы соответствуют перестановкам шести элементов, из которых определяем морфемы и наборы. Эти перестановки действуют на граф Татта — Коксетера путём перестановок вершин на каждой доле двудольного графа, сохранная каждую долю как множество. Вдобавок, внешние автоморфизмы группы перестановок переставляют местами доли двудольного графа. Как показал Коксетер, любой путь длиной до пяти рёбер графа Татта — Коксетера эквивалентен любому другому такому пути (то есть переводятся из одного в другой с помощью одного из таких автоморфизмов).
Галерея
 Число пересечений графа Татта — Коксетера равно 13.
Число пересечений графа Татта — Коксетера равно 13. Хроматическое число графа Татта — Коксетера равно 2.
Хроматическое число графа Татта — Коксетера равно 2.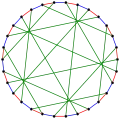 хроматический индекс графа Татта — Коксетера равен 3.
хроматический индекс графа Татта — Коксетера равен 3.
Примечания
- Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance — Regular Graphs. New York: Springer—Verlag, 1989.
Литература
- H. S. M. Coxeter. The chords of the non-ruled quadric in PG(3,3) // Canad. J. Math. — 1958. — Т. 10. — С. 484—488. — doi:10.4153/CJM-1958-047-0.
- H. S. M. Coxeter. Twelve points in PG(5,3) with 95040 self-transformations // Proceedings of the Royal Society A. — 1958. — Т. 247, вып. 1250. — С. 279—293. — doi:10.1098/rspa.1958.0184. — .
- J. J. Sylvester. Elementary researches in the analysis of combinatorial aggregation // The Philos. Mag., Series 3. — 1844. — Т. 24. — С. 285—295.
- W. T. Tutte. A family of cubical graphs // Proc. Cambridge Philos. Soc. — 1947. — Т. 43, вып. 04. — С. 459—474. — doi:10.1017/S0305004100023720.
- W. T. Tutte. The chords of the non-ruled quadric in PG(3,3) // Canad. J. Math. — 1958. — Т. 10. — С. 481—483. — doi:10.4153/CJM-1958-046-3.
Ссылки
- François Labelle. 3D Model of Tutte's 8-cage.
- Weisstein, Eric W. Levi Graph (англ.) на сайте Wolfram MathWorld.
- Exoo, G. «Rectilinear Drawings of Famous Graphs.»