Ациклическая раскраска графа
В теории графов под ациклической раскраской понимается (правильная) раскраска вершин, в которой любой двуцветный подграф не имеет циклов. Ациклическим хроматическим числом A(G) графа G называется наименьшее число цветов, необходимое в любой ациклической раскраске G.
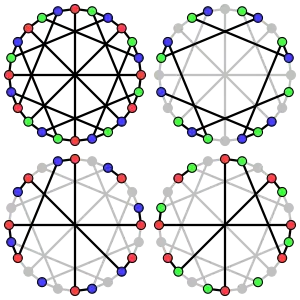
Ациклическая раскраска часто связывается с графами на поверхностях, не являющихся плоскостями.
Верхние границы
A(G) ≤ 2 тогда и только тогда, когда G не имеет циклов.
Границы A(G) в терминах максимальной степени Δ(G) графа G включают следующие:
- A(G) ≤ 4 если Δ(G) = 3. (Grünbaum 1973)
- A(G) ≤ 5 если Δ(G) = 4. (Burstein 1979)
- A(G) ≤ 8 если Δ(G) = 5.(Yadav, Satish 2008)
- A(G) ≤ 12 если Δ(G) = 6.(Yadav, Satish 2009)
Вехой в изучении ациклической раскраски является следующий положительный ответ на гипотезу Грюнбаума:
Теорема. (Borodin 1979)
- A(G) ≤ 5 если G планарен.
Грюнбаум (1973) ввёл ациклическую раскраску и ациклическое хроматическое число и высказал гипотезу, которая и была доказана Бородиным. На доказательство у Бородина ушло несколько лет старательной проверки 450 конфигураций. Одним из следствий этой теоремы является то, что любой планарный граф можно разложить на независимое множество и два леса. (Stein 1970, 1971)
Алгоритмы и сложность
Задача определения, выполняется ли A(G) ≤ 3, является NP-полной (Kostochka 1978). Коулман и Цай (Coleman, Cai 1986) показали, что задача остаётся NP-полной даже для двудольных графов.
Гебремедхин и др. (Gebremedhin, Tarafdar, Pothen, Walther 2008) продемонстрировали, что любая правильная вершинная раскраска хордального графа является ациклической раскраской. Поскольку для хордальных графов можно найти оптимальную раскраску за время O(n+m), то же самое верно и для ациклической раскраски на этом классе графов.
Линейный по времени алгоритм для ациклической раскраски графа максимальной степени ≤ 3 в 4 цвета или меньше представлена Скулраттанакулчаем (Skulrattanakulchai 2004). Ядав и Сатиш (Yadav, Satish 2008) описывают линейный по времени алгоритм ациклической раскраски графа с максимальной степенью ≤ 5 при использовании 8 цветов и менее, а также алгоритм раскраски графа максимальной степени ≤ 6 при использовании 12 цветов и менее.
См. также
Замечания
Ссылки
- O. V. Borodin. On acyclic colorings of planar graphs // Discrete Mathematics. — 1979. — Т. 25. — С. 211–236. — doi:10.1016/0012-365X(79)90077-3..
- M. I. Burstein. Every 4-valent graph has an acyclic 5-coloring (in Russian) // Soobšč. Akad. Nauk Gruzin. SSR. — 1979. — Т. 93. — С. 21–24.
- B. Grünbaum. Acyclic colorings of planar graphs // Israel J. Math.. — 1973. — Т. 14. — С. 390–408. — doi:10.1007/BF02764716.
- Thomas F. Coleman, Jin-Yi Cai. The Cyclic Coloring Problem and Estimation of Sparse Hessian Matrices // SIAM. J. on Algebraic and Discrete Methods. — 1986. — Т. 7. — С. 221–235. — doi:10.1137/0607026..
- Guillaume Fertin, André Raspaud. Acyclic coloring of graphs of maximum degree five: Nine colors are enough // Information Processing Letters. — 2008. — Т. 105. — С. 65–72. — doi:10.1016/j.ipl.2007.08.022..
- Kishore Yadav, Venkaiah Satish. Acyclic coloring of graphs of maximum degree five: Eight colors are enough // ICGTA. — 2008. — Т. nil. — С. nil..
- Kishore Yadav, Venkaiah Satish, Kishore Yadav, Kishore Kothapalli. Acyclic coloring of graphs of maximum degree six: Twelve colors are enough // Electronic Notes in Discrete Mathematics. — 2009. — Т. 35. — С. 177–182. — doi:10.1016/j.endm.2009.11.030..
- Assefaw H. Gebremedhin, Arijit Tarafdar, Alex Pothen, Andrea Walther. Efficient Computation of Sparse Hessians Using Coloring and Automatic Differentiation // Informs Journal on Computing. — 2008. — Т. 21. — С. 209. — doi:10.1287/ijoc.1080.0286..
- Jensen, Tommy R.; Toft, Bjarne (1995). Graph coloring problems. New York: Wiley-Interscience. ISBN 0-471-02865-7.
- Kostochka, A. V. (1978). Upper bounds of chromatic functions of graphs (in Russian). Doctoral thesis, Novosibirsk.
- San Skulrattanakulchai. Acyclic colorings of subcubic graphs // Information Processing Letters. — 2004. — Т. 92. — С. 161–167. — doi:10.1016/j.ipl.2004.08.002..
- S. K. Stein. B-sets and coloring problems // Bull. Amer. Math. Soc.. — 1970. — Т. 76. — С. 805–806. — doi:10.1090/S0002-9904-1970-12559-9.
- S. K. Stein. B-sets and planar maps // Pacific J. Math.. — 1971. — Т. 37. — С. 217–224.
Внешние ссылки
- Star colorings and acyclic colorings (1973), present at the Research Experiences for Graduate Students (REGS) at the University of Illinois, 2008.
- Acyclic Coloring of Graphs of Maximum Degree ∆, talk slides presented by G. Fertin and A. Raspaud at EUROCOMB 05, Berlin, 2005.