Звёздная раскраска

Звёздная раскраска в теории графов — (правильная) раскраска вершин, в которой любой путь из четырёх вершин использует как минимум три различных цвета. Эквивалентное определение — это такая раскраска, при которой любые компоненты связности порождённых подграфов, образованных вершинами любых двух цветов, являются звёздами. Звёздная раскраска была предложена Грюнбаумом[1].

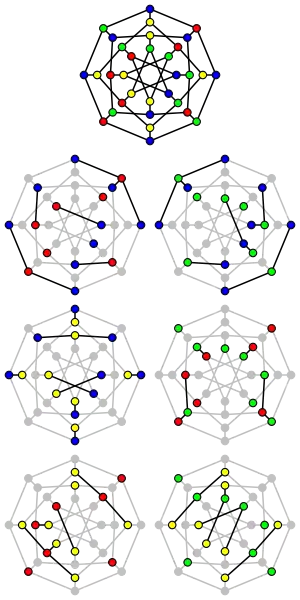
Звёздное хроматическое число графа Дика равно 4, в то время как его хроматическое число равно 2.

Звёздное хроматическое число ${\displaystyle \chi _{s}(G)}$ графа ${\displaystyle G}$ — это минимальное число цветов, необходимых для получения звёздной раскраски ${\displaystyle G}$.

Одно из обобщений звёздной раскраски тесно связано с концепцией ациклической раскраски графа, в которой требуется, чтобы любой цикл использовал по меньшей мере три цвета, так что порождённые парой цветов подграфы образуют леса. Хроматическое число графа ${\displaystyle \chi _{a}(G)}$ не превосходит звёздное хроматическое число ${\displaystyle \chi _{s}(G)}$, что фактически означает, что любая звёздная раскраска графа ${\displaystyle G}$ является ациклической раскраской.

Доказано, что звёздное хроматическое число ограничено для любого минорно замкнутого класса[2]. Этот результат позднее был обобщён [3] для всех раскрасок с малой глубиной деревьев (обычная раскраска и звёздная раскраска являются раскрасками с малой глубиной деревьев с параметрами 1 и 2 соответственно).

Было показано[4], что проверка выполнения неравенства ${\displaystyle \chi _{s}(G)\leqslant 3}$, является NP-полной задачей, даже если граф ${\displaystyle G}$ одновременно и планарен, и двудолен. Коулмэн и Морэ[5] показали, что поиск оптимальной звёздной раскраски является NP-трудной задачей, даже если ${\displaystyle G}$ является двудольным графом.