Градуированное частично упорядоченное множество

Несколько примеров градуированных ЧУМ (с функциями ранга):

• натуральные числа N с их естественным порядком (ранг — само число) или некоторый интервал [0,N] этого ЧУМ,
• Nⁿ с порядком прямого приведения или подмножество этого ЧУМ, являющееся произведением интервалов,
• положительные числа, упорядоченные по числу простых делителей с учётом кратности или подмножество этого ЧУМ, образованное делителями фиксированного числа N,
• булева решётка конечных подмножеств множества (ранг — число элементов в подмножестве),
• решётка разбиений множества на конечное число частей, упорядоченная обратно степени разбиения (ранговая функция — число частей),
• решётка разбиений конечного множества X, упорядоченная по степени разбиения (ранговая функция — число элементов X минус число частей разбиения),
• группа и порождающее множество, или, эквивалентно, её граф Кэли, порядок — слабый или сильный порядок Брухата, ранговая функция — длина слова (длина самого короткого приведённого слова).
  • в частности, для групп Коксетера, например, перестановок вполне упорядоченного множества из n-элементов, со слабым или сильным порядком Брухата (ранговая функция — число смежных инверсий),
• геометрические решётки, такие как решётка подпространств векторного пространства (ранговая функция — размерность подпространства),
• дистрибутивная решётка конечного нижнего множества другого ЧУМ (ранговая функция — число элементов),
• решётка Юнга, частный случай предыдущего примера (ранговая функция — число ячеек в диаграмме Юнга),
• решётки граней многомерных выпуклых многогранников (ранговая функция — размерность грани + 1),
• абстрактные многогранники (ранговая функция — «расстояние» от наименьшей грани - 1),
• абстрактные симплициальные комплексы (ранговая функция — число элементов симплекса).

Решётка N₅ не может быть градуирована.

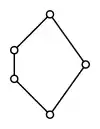
Ограниченное частично упорядоченное множество[3] допускает градуирование тогда и только тогда, когда все максимальные цепочки в P имеют одну длину [4] — если установить ранг наименьшего элемента равным 0, то ранг определяется полностью. Это перекрывает много конечных случаев. См. рисунок примера, не допускающего градуирования. Неограниченные ЧУМ, однако, могут быть существенно сложнее.

Функция-кандидат ранга, совместимая с упорядочением, делает ЧУМ градуированным тогда и только тогда, когда для x < z, где z имеет ранг n+1, для всех элементов y ранга n должно выполняться x ≤ y < z. Это условие является достаточным, поскольку в случае, когда x подчинён z, единственная возможность — y = x, и условие является необходимым, поскольку в градуированном ЧУМ можно в качестве y взять любой элемент максимального ранга с x ≤ y < z, который всегда существует и подчинён z.

Часто получаем ЧУМ с естественным кандидатом для ранговой функции. Например, если его элементы являются подмножествами некоторого базового множества B, можно взять число элементов этих подмножеств. Тогда выше указанный критерий может оказаться более практичным, чем определение, поскольку в нём не упоминается подчинение. Например, если B само по себе является ЧУМ-ом и P состоит из конечных нижних множеств (подмножества, для которых для любого элемента подмножества все меньшие элементы принадлежат тому же множеству), тогда это условие автоматически удовлетворяется, поскольку для нижних множеств x ⊂ z всегда существует максимальный элемент множества z, который отсутствует в x и может быть удалён из z для получения y.

В некоторых общих ЧУМ, таких как решётки граней выпуклых многограников, существует естественное градуирование (размерность), которое, будучи использованным в качестве функции ранга, даёт минимальный элемент, пустую грань с рангом –1. В таких случаях удобно «подправить» определение выше путём добавления значения –1 к множеству допустимых значений функции ранга. Если же позволить функции ранга принимать произвольные целые значения, получим совсем другое понятие. В этом случае, например, нельзя говорить о существовании минимального элемента.

Градуированное ЧУМ (с положительными значениями функции ранга) не может имеет какого-либо элемента x, до которого существуют цепочки произвольной длины с максимальным элементом x, в противном случае оно имело бы элементы произвольно малого (в том числе и отрицательного) ранга. Например, множество целых чисел (с естественным порядком) не может быть градуированным ЧУМ. Не может быть градуированным ЧУМ любой интервал (более чем с одним элементом), рациональных или вещественных чисел. (В частности, градуированные ЧУМ являются вполне фундированными, что означает, что они удовлетворяют условию убывающей цепочки — они не содержат какой-либо бесконечной убывающей цепи [5]). С этого момента мы рассматриваем ЧУМы , в которых таких цепочек нет. Отсюда следует, что при x < y мы можем получить y из x за конечное число шагов, последовательно выбирая элемент, которому предыдущий элемент подчинён. Это также означает, что (для функций ранга, принимающих положительные целые значения) совместимость ρ с порядком следует из требования подчинённости. В качестве варианта определения градуированного ЧУМ Биркгоф[6] позволяет функции ранга иметь произвольные (а не только неотрицательные) целые значения. В этом варианте целые числа могут быть градуированы (с помощью тождественной функции) и совместимость функции ранга с порядком не является избыточным требованием.

Заметим, что градуированное ЧУМ не обязано удовлетворять условию возрастающей цепочки. Например, натуральные числа содержат бесконечную возрастающую цепочку ${\displaystyle 0<1<2<\cdots }$.

ЧУМ является градуированным тогда и только тогда, когда любая связная компонента его графа сравнимости является градуированной, так что дальнейшее описание предполагает, что этот граф сравнимости связен. На каждой связной компоненте функция ранга единственна с точностью до однородного сдвига (так что функцию ранга можно всегда выбрать так, что минимальный ранг связной компоненты имеет ранг 0).

Если P имеет наименьший элемент Ô, при градуировании это эквивалентно условию, что для любого элемента x все максимальные цепи в интервале [Ô,x] имеют одну и ту же длину. Это условие необходимо, поскольку любой шаг в максимальной цепи является отношением подчинения, которое изменяет ранг на 1. Условие является также достаточным, поскольку в случае его выполнения можно использовать упомянутую длину для определения ранга x (длина конечной цепи равно числу "шагов", так что ранг на единицу меньше числа элементов цепи), и когда y подчинён x, добавление x к максимальной цепи [Ô,y] даёт максимальную цепь в [Ô,x].

Если P имеет также наибольший элемент Î (так что это ограниченное ЧУМ), тогда предыдущее условие может быть упрощено до требования, что все максимальные цепи в P имеют одну и ту же (конечную) длину. Это условие достаточно, поскольку любая пара максимальных цепей в [Ô,x] могут быть расширены максимальной цепью в [x,Î], что даёт пару максимальных цепей в P.

Примечание Ричард Стэнли определяет ЧУМ градуированным с длиной n, если его максимальные цепи имеют длину n[7]. Это определение даётся в контексте, где, в основном, рассматриваются конечные ЧУМ, и, хотя в книге часто слова «длины n» опущены, для ЧУМ общего вида это определение не выглядит приемлемым, поскольку (1) оно ничего не говорит о ЧУМ, имеющих бесконечные максимальные цепи, и (2) оно исключает важные ЧУМ, такие как решётки Юнга. Также не ясно, почему в градуированном ЧУМ все минимальные элементы, как и все максимальные элементы, должны иметь одну и ту же длину, хотя Стэнли даёт примеры, по которым ясно, что он не требует этого (там же, стр.216 и 219).

Многие авторы в области комбинаторики определяют градуированное ЧУМ таким образом, что все минимальные элементы P должны иметь ранг 0, и более того, что существует максимальный ранг r, являющийся рангом любого максимального элемента. В этом случае градуирование означает, что все максимальные цепи имеют длину r, как сказано выше. В этом случае говорят, что P имеет ранг r.

Далее, в этом случае с уровнем ранга связываются ранговые числа, или числа Уитни ${\displaystyle W_{0},W_{1},W_{2},...}$. Эти числа определяются как ${\displaystyle W_{i}}$ = число элементов множества P, имеющих ранг i .

Числа Уитни связаны со множеством важных комбинаторных теорем. Классический пример — теорема Спернера, которую можно сформулировать следующим способом:

Для степени ${\displaystyle {\mathcal {P}}(S)}$ любого конечного множества ${\displaystyle S}$ максимальная мощность семейства Спернера равна максимальному числу Уитни.

Это означает, что

Любая конечная степень множества имеет свойство Спернера

• Предупорядочение – предупорядочение с нормой является аналогом градуированного ЧУМ, где отображение в целые числа заменяется на порядковые числа
• Звёздное произведение, метод комбинирования двух градуированных ЧУМ