Гиперболическая неподвижная точка
Гиперболическая неподвижная точка (гиперболическая точка) — фундаментальное понятие, использующееся в теории динамических систем по отношению к отображениям (диффеоморфизмам) и векторным полям. В случае отображения гиперболической точкой называется неподвижная точка, в которой все мультипликаторы (собственные числа линеаризации отображения в данной точке) по модулю отличны от единицы. В случае векторных полей гиперболической точкой называется особая точка, в которой все собственные числа линеаризации поля имеют ненулевые вещественные части.
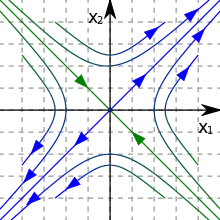
Устойчивое и неустойчивое многообразия
В гиперболической точке векторного поля (или диффеоморфизма) касательное пространство раскладывается в прямую сумму двух инвариантных подпространств и , инвариантных относительно оператора линейной части поля: . Подпространства и определяются соответственно условиями , в случае векторных полей и условиями , в случае диффеоморфизмов. Эти подпространства являются инвариантными многообразиями линеаризованного векторного поля (диффеоморфизма) в данной точке, они называются его неустойчивым и устойчивым, соответственно.
Неустойчивым и устойчивым многообразиями исходного нелинейного векторного поля (диффеоморфизма) называются его инвариантные многообразия и , касающиеся соответственно подпространств и в рассматриваемой точке и имеющие те же размерности, что и . Многообразия и определяются единственным образом[1]. Отметим, что многообразия и существуют не только в случае гиперболических особых точек, однако в случае гиперболической точки сумма их размерностей равна размерности всего пространства, и других инвариантных многообразий, проходящих через данную особую точку, не существует[1].
Теоремы о гиперболических точках
Теорема Гробмана — Хартмана. В окрестности гиперболической точки нелинейного диффеоморфизма (векторного поля) динамика отличается от таковой для соответствующего линейного отображения (векторного поля) непрерывной заменой координат.
Теорема Адамара — Перрона.[2][3] В окрестности гиперболической точки гладкого (или аналитического) векторного поля или диффеоморфизма существуют неустойчивое и устойчивое многообразия и такого же класса гладкости (соответственно, аналитические), проходящие через данную точку.
Теорема Ченя.[4][5] Если в окрестности гиперболической точки два -гладких векторных поля (диффеоморфизма) формально эквивалентны (т.е. переводятся друг в друга посредством формальной замены переменных, заданной формальными степенными рядами), то они -гладко эквивалентны.
Литература
- Я. Г. Синай. Современные проблемы эргодической теории, — М.: Физматлит, 1995 (c. 137).
- В. И. Арнольд, Ю. С. Ильяшенко. Обыкновенные дифференциальные уравнения, Динамические системы – 1, Итоги науки и техн. Сер. Соврем. пробл. мат. Фундам. направления, 1, ВИНИТИ, М., 1985, 7–140
- Марсден Дж., Мак Кракен М. Бифуркация рождения цикла и ее приложения. М.: Мир, 1980.
- Ильяшенко Ю.С., Вейгу Л. Нелокальные бифуркации. — М.: МЦНМО-ЧеРо, 1999. — 416 с. — ISBN 5-900916-34-0.
- Каток А. Б., Хассельблат Б. Введение в современную теорию динамических систем с обзором последних достижений / Пер. с англ. под ред. А. С. Городецкого. — М.: МЦНМО, 2005. — 464 с. — ISBN 5-94057-063-1.
Примечания
- В. И. Арнольд, Ю. С. Ильяшенко. Обыкновенные дифференциальные уравнения, Динамические системы – 1, Итоги науки и техн. Фундам. направления, 1, ВИНИТИ, М., 1985, глава 3.
- В. И. Арнольд, Ю. С. Ильяшенко. Обыкновенные дифференциальные уравнения, Динамические системы – 1, Итоги науки и техн. Фундам. направления, 1, ВИНИТИ, М., 1985, стр. 61.
- Марсден Дж., Мак Кракен М. Бифуркация рождения цикла и ее приложения. М.: Мир, 1980.
- В. И. Арнольд, Ю. С. Ильяшенко. Обыкновенные дифференциальные уравнения, Динамические системы – 1, Итоги науки и техн. Фундам. направления, 1, ВИНИТИ, М., 1985, стр. 72.
- Chen, Kuo-Tsai. Equivalence and decomposition of vector fields about an elementary critical point. Amer. J. Math. 85 (1963), p. 693-722.