Особая точка (дифференциальные уравнения)

В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.

В любой малой окрестности фазового пространства, не содержащей особых точек, векторное поле можно выпрямить подходящей заменой координат — тем самым, поведение системы вне особых точек устроено одинаково и очень просто. Напротив, в окрестности особой точки система может обладать очень сложной динамикой. Говоря о свойствах особых точек векторных полей, обычно подразумевают свойства соответствующей системы в малой окрестности особой точки.

Особые точки векторных полей на плоскости

Простейшими примерами особых точек являются особые точки линейных векторных полей на плоскости. С понятием векторного поля на плоскости можно связать линейную систему дифференциальных уравнений вида:

${\dot {x}}=Ax$ ,

где $x=(x_{1},x_{2})$ — точка на плоскости, $A$ — матрица $2\times 2$ . Очевидно, точка $x=(0,0)$ в случае невырожденной матрицы $A$ является единственной особой точкой такого уравнения.

В зависимости от собственных значений матрицы $A$ , различают четыре типа невырожденных особых точек линейных систем: узел, седло, фокус, центр.

Тип собственных значений	Тип особой точки	Тип фазовых траекторий
Чисто мнимые	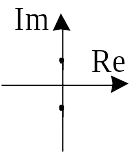Центр	окружности, эллипсы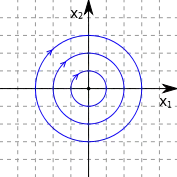
Комплексные с отрицательной действительной частью	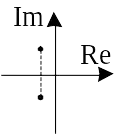Устойчивый фокус	Логарифмические спирали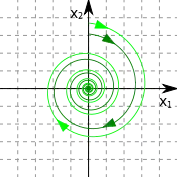
Комплексные с положительной действительной частью	Неустойчивый фокус	Логарифмические спирали
Действительные отрицательные	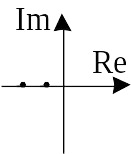Устойчивый узел	параболы
Действительные положительные	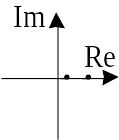Неустойчивый узел	параболы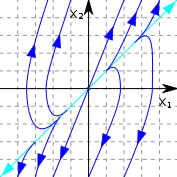
Действительные разных знаков	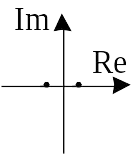Седло	гиперболы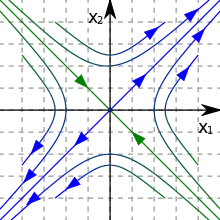

См. также

Теорема Пуанкаре о векторном поле

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.