Вынужденные колебания

Второй закон Ньютона для такого осциллятора запишется в виде: ${\displaystyle ma=-kx+F_{0}\cos \left(\Omega t\right)}$. Если ввести обозначения: ${\displaystyle \omega _{0}^{2}={\frac {k}{m}},\quad \Phi _{0}={\frac {F_{0}}{m}}}$ и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

${\displaystyle {\ddot {x}}+\omega _{0}^{2}x=\Phi _{0}\cos(\Omega t)}$

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:

${\displaystyle x(t)=A\sin \left(\omega _{0}t+\varphi \right)}$,

где ${\displaystyle A,\varphi }$ — произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида: ${\displaystyle x(t)=B\cos \left(\Omega t\right)}$ и получим значение для константы:

${\displaystyle B={\frac {\Phi _{0}}{\omega _{0}^{2}-\Omega ^{2}}}}$

Тогда окончательное решение запишется в виде:

${\displaystyle x(t)=A\sin \left(\omega _{0}t+\varphi \right)+{\frac {\Phi _{0}}{\omega _{0}^{2}-\Omega ^{2}}}\cos \left(\Omega t\right)}$

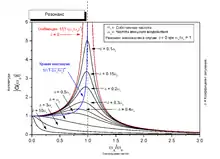
Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания

Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде: ${\displaystyle x(t)=t\left(A\cos \left(\Omega t\right)+B\sin \left(\Omega t\right)\right)}$. Подставим этот анзац в дифференциальное уравнение и получим, что

${\displaystyle A=0\qquad B={\frac {\Phi _{0}}{2\Omega }}}$

Таким образом, колебания в резонансе будут описываться следующим соотношением:

${\displaystyle x(t)={\frac {\Phi _{0}}{2\Omega }}t\sin \left(\Omega t\right)}$

Второй закон Ньютона:

${\displaystyle ma=-kx-\alpha v+F_{0}\cos \left(\Omega t\right)}$.

Переобозначения:

${\displaystyle \omega _{0}^{2}={\frac {k}{m}},\qquad \Phi _{0}={\frac {F_{0}}{m}},\qquad \zeta ={\frac {\alpha }{2{\sqrt {km}}}}}$

Дифференциальное уравнение:

${\displaystyle {\ddot {x}}+2\zeta \omega _{0}{\dot {x}}+\omega _{0}^{2}x=\Phi _{0}\cos \left(\Omega t\right)}$

Его решение будет строиться, как сумма решений однородного уравнения и частного решения неоднородного. Анализ однородного уравнения приведён здесь. Получим и проанализируем частное решение.

Запишем вынуждающую силу следующим образом: ${\displaystyle \Phi _{0}\cos \Omega t=\Phi _{0}Re\,e^{-i\Omega t}}$, тогда решение будем искать в виде: ${\displaystyle x(t)=Ae^{-i\Omega t}}$, где ${\displaystyle A\in \mathbb {C} }$. Подставим это решение в уравнение и найдём выражение для ${\displaystyle A}$:

${\displaystyle A={\frac {\Phi _{0}}{\omega _{0}^{2}-\Omega ^{2}-2i\zeta \Omega }}={\frac {\Phi _{0}\left(\omega _{0}^{2}-\Omega ^{2}+2i\zeta \Omega \right)}{\left(\omega _{0}^{2}-\Omega ^{2}\right)^{2}+4\zeta ^{2}\Omega ^{2}}}=|A|e^{-i\varphi }}$

где ${\displaystyle |A|={\frac {\Phi _{0}}{\sqrt {\left(\omega _{0}^{2}-\Omega ^{2}\right)^{2}+4\zeta ^{2}\Omega ^{2}}}},\qquad \varphi =-\arctan {\frac {2\zeta \Omega }{\omega _{0}^{2}-\Omega ^{2}}}}$

Полное решение имеет вид:

${\displaystyle x(t)=e^{-\zeta \omega _{0}t}(c_{1}\cos(\omega _{\mathrm {d} }t)+c_{2}\sin(\omega _{\mathrm {d} }t))+Re\left[{\frac {\Phi _{0}\left(\omega _{0}^{2}-\Omega ^{2}+2i\zeta \Omega \omega _{0}\right)}{\left(\omega _{0}^{2}-\Omega ^{2}\right)^{2}+4\zeta ^{2}\Omega ^{2}\omega _{0}^{2}}}e^{-i\Omega t}\right]}$,

где ${\displaystyle \omega _{\mathrm {d} }=\omega _{0}{\sqrt {1-\zeta ^{2}}}}$ — собственная частота затухающих колебаний.

Константы ${\displaystyle c_{1}}$ и ${\displaystyle c_{2}}$ в каждом из случаев определяются из начальных условий: ${\displaystyle \left\{{\begin{array}{ccc}x(0)&=&x_{0}\\{\dot {x}}(0)&=&v_{0}\end{array}}\right.}$

В этом случае, в отличие от осциллятора без трения, амплитуда колебаний в резонансе имеет конечную величину.

Если мы рассмотрим устоявший процесс, то есть ситуацию при ${\displaystyle t\,\to \,\infty }$, то решение однородного уравнения будет стремиться к нулю и останется только частное решение:

${\displaystyle x(t\to \infty )=\Phi _{0}{\frac {\left(\omega _{0}^{2}-\Omega ^{2}\right)\cos {\Omega t}+2\zeta \Omega \sin {\Omega t}}{\left(\omega _{0}^{2}-\Omega ^{2}\right)^{2}+4\zeta ^{2}\Omega ^{2}}}={\frac {\Phi _{0}}{\sqrt {(\omega _{0}^{2}-\Omega ^{2})^{2}+4\zeta ^{2}\omega _{0}^{2}\Omega ^{2}}}}\cos(\Omega t-\varphi )}$

Это означает, что при ${\displaystyle t\,\to \,\infty }$ система «забывает» начальные условия, и характер колебаний зависит только от вынуждающей силы.

Работа, совершаемая вынуждающей силой ${\displaystyle F(t)=F_{0}\cos \left(\Omega t\right)}$ за время ${\displaystyle dt\ }$, равна ${\displaystyle Fdx\ }$, а мощность ${\displaystyle P=F{\frac {dx}{dt}}}$. Из уравнения

${\displaystyle {\ddot {x}}+2\zeta \omega _{0}{\dot {x}}+\omega _{0}^{2}x=\Phi _{0}\cos \left(\Omega t\right)}$

следует, что

${\displaystyle P(t)=F{\dot {x}}=({\ddot {x}}+2\zeta \omega _{0}{\dot {x}}+\omega _{0}^{2}x)m{\dot {x}}}$

Если учесть, что при установившихся вынужденных колебаниях

${\displaystyle x\,=A\,\cos(\Omega t-\varphi )}$

${\displaystyle {\dot {x}}=-A\Omega \sin(\Omega t-\varphi )}$

${\displaystyle {\ddot {x}}=-A\Omega ^{2}\cos(\Omega t-\varphi )}$

то тогда средняя за период ${\displaystyle T={\frac {2\pi }{\Omega }}}$ мощность:

${\displaystyle P={\frac {m}{T}}\int _{0}^{T}({\ddot {x}}+2\zeta \omega _{0}{\dot {x}}+\omega _{0}^{2}x){\dot {x}}dt=A^{2}m\zeta \omega _{0}\Omega ^{2}}$

Работа за период

${\displaystyle W=m\int _{0}^{T}({\ddot {x}}+2\zeta \omega _{0}{\dot {x}}+\omega _{0}^{2}x){\dot {x}}dt=A^{2}m\zeta \omega _{0}\Omega ^{2}T=2\pi A^{2}m\zeta \omega _{0}\Omega }$