Быстрый обратный квадратный корень

Бы́стрый обра́тный квадра́тный ко́рень (также быстрый InvSqrt() или 0x5F3759DF по используемой «магической» константе) — это быстрый приближённый алгоритм вычисления обратного квадратного корня $y={\frac {1}{\sqrt {x}}}$ для положительных 32-битных чисел с плавающей запятой. Алгоритм использует целочисленные операции «вычесть» и «битовый сдвиг», а также дробные «вычесть» и «умножить» — без медленных операций «разделить» и «квадратный корень». Несмотря на «хакерство» на битовом уровне, приближение монотонно и непрерывно: близкие аргументы дают близкий результат. Точности (менее 0,2 % в меньшую сторону и никогда — в большую)[1][2] не хватает для настоящих численных расчётов, однако вполне достаточно для трёхмерной графики.

При расчёте освещения OpenArena (свободный порт Quake III: Arena) вычисляет углы падения и отражения через быстрый обратный квадратный корень. Обратите внимание на кожух оружия — при очень низкой детализации (8 четырёхугольников) игра делает вид, что он криволинейный.

Алгоритм

Алгоритм принимает 32-битное число с плавающей запятой (одинарной точности в формате IEEE 754) в качестве исходных данных и производит над ним следующие операции:

Трактуя 32-битное дробное число как целое, провести операцию y₀ = 5F3759DF₁₆ − (x >> 1), где >> — битовый сдвиг вправо. Результат снова трактуется как 32-битное дробное число.
Для уточнения можно провести одну итерацию метода Ньютона: y₁ = y₀(1,5 − 0,5xy₀²).

Корректная по меркам современного Си реализация, с учётом возможных оптимизаций и кроссплатформенности:

float Q_rsqrt( float number )
{	
	const float x2 = number * 0.5F;
	const float threehalfs = 1.5F;

	union {
		float f;
		uint32_t i;
	} conv = {number}; // member 'f' set to value of 'number'.
	conv.i = 0x5f3759df - ( conv.i >> 1 );
	conv.f *= threehalfs - x2 * conv.f * conv.f;
	return conv.f;
}

Реализация из Quake III: Arena[3] считает, что float по длине равен long, и использует для преобразования указатели (может ошибочно сработать оптимизация «если изменился float, ни один long не менялся»; на GCC при компиляции в «выпуск» срабатывает предупреждение). А ещё она содержит нецензурное слово — Джон Кармак, выкладывая игру в открытый доступ, не понял, что там делается.

История

Алгоритм был, вероятно, разработан в Silicon Graphics в 1990-х, а реализация появилась в 1999 году в исходном коде компьютерной игры Quake III Arena, но данный метод не появлялся на общедоступных форумах, таких как Usenet, до 2002—2003-х годов. Алгоритм генерирует достаточно точные результаты, используя уникальное первое приближение метода Ньютона. В то время основным преимуществом алгоритма был отказ от дорогих вычислительных операций с плавающей запятой в пользу целочисленных операций. Обратные квадратные корни используются для расчета углов падения и отражения для освещения и затенения в компьютерной графике.

Алгоритм изначально приписывался Джону Кармаку, но тот предположил, что его в id Software принёс Майкл Абраш, специалист по графике, или Терье Матисен, специалист по ассемблеру[4]. Изучение вопроса показало, что код имел более глубокие корни как в аппаратной, так и в программной сферах компьютерной графики. Исправления и изменения производились как Silicon Graphics, так и 3dfx Interactive, при этом самая ранняя известная версия написана Гэри Таролли для SGI Indigo. Возможно, алгоритм придумали Грег Уолш и Клив Моулер, коллеги Гэри по Ardent Computer[5].

С выходом в свет в 1998 году набора инструкций 3DNow! в процессорах фирмы AMD появилась ассемблерная инструкция PFRSQRT[6] для быстрого приближенного вычисления обратного квадратного корня. Версия для double бессмысленна — точность вычислений не увеличится[2] — потому её не добавили. В 2000 году в SSE2 добавили функцию RSQRTSS[7] более точную, чем данный алгоритм (0,04 % против 0,2 %).

Анализ и погрешность

Битовое представление 4-байтового дробного числа в формате IEEE 754 выглядит так:

Знак
	Порядок								Мантисса
0	0	1	1	1	1	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	$=(1+2^{-2})\cdot 2^{-3}=0{,}15625$
31				24				23				16				15				8				7				0

\log _{2}(1+m_{x})\approx m_{x}+\sigma

. Приведены крайние случаи — σ = 0 и 0,086.

Имеем дело только с положительными числами (знаковый бит равен нулю), не денормализованными, не ∞ и не NaN. Такие числа в стандартном виде записываются как 1,mmmm₂·2^e. Часть 1,mmmm называется мантиссой, e — порядком. Головную единицу не хранят (неявная единица), так что величину 0,mmmm назовём явной частью мантиссы. Кроме того, у машинных дробных чисел смещённый порядок: 2⁰ записывается как 011.1111.1₂.

На положительных числах биекция «дробное ↔ целое» (ниже обозначенная как $I_{x}$ ) непрерывна как кусочно-линейная функция и монотонна. Отсюда сразу же можно заявить, что быстрый обратный корень, как комбинация непрерывных функций, непрерывен. А первая его часть — сдвиг-вычитание — к тому же монотонна и кусочно-линейна. Биекция сложна, но почти «бесплатна»: в зависимости от архитектуры процессора и соглашений вызова, нужно или ничего не делать, или переместить число из дробного регистра в целочисленный.

Например, двоичное представление 16-ричного целого числа 0x5F3759DF есть 0|101.1111.0|011.0111.0101.1001.1101.1111₂ (Точки — границы полубайтов, вертикальные линии — границы полей компьютерного дробного). Порядок 101 1111 0₂ равен 190₁₀, после вычитания смещения 127₁₀ получаем показатель степени 63₁₀. Явная часть мантиссы 01 101 110 101 100 111 011 111₂ после добавления неявной ведущей единицы превращается в 1,011 011 101 011 001 110 111 11₂ = 1,432 430 148…₁₀. С учётом реальной точности компьютерных дробных 0x5F3759DF ↔ 1,4324301₁₀·2⁶³.

Обозначим $m_{x}\in [0,1)$ явную часть мантиссы числа $x$ , $e_{x}\in \mathbb {Z}$ — несмещённый порядок, $L=2^{23}$ — разрядность мантиссы, $B=127$ — смещение порядка. Число $x\equiv 2^{e_{x}}(1+m_{x})$ , записанное в линейно-логарифмической разрядной сетке компьютерных дробных, можно[8][3] приблизить логарифмической сеткой как $\log _{2}x\equiv e_{x}+\log _{2}(1+m_{x})\approx e_{x}+m_{x}+\sigma$ , где $\sigma$ — параметр, используемый для настройки точности приближения. Этот параметр варьируется от 0 (формула точна при $m_{x}=0$ и $1$ ) до 0,086 (точна в одной точке, $m_{x}=0{,}443$ )

Воспользовавшись этим приближением, целочисленное представление числа $x$ можно приблизить как

I_{x}\equiv L(e_{x}+B+m_{x})\approx L\log _{2}x+L(B-\sigma )

Соответственно, $\log _{2}x\approx {\frac {I_{x}}{L}}-(B-\sigma )$ .

Проделаем это же[3] для $y={\tfrac {1}{\sqrt {x}}}$ (соответственно $\log _{2}y=-{\tfrac {1}{2}}\log _{2}x$ ), и получим

I_{y}\approx {\tfrac {3}{2}}L(B-\sigma )-{\tfrac {1}{2}}I_{x}

y\approx I^{-1}\left[{\tfrac {3}{2}}L(B-\sigma )-{\tfrac {1}{2}}I_{x}\right]

Магическая константа ${\tfrac {3}{2}}L(B-\sigma )$ , с учётом границ $\sigma$ , в арифметике дробных чисел имеет вид $c\cdot 2^{63}$ , где $c=1{,}5-1{,}5\sigma \in (1{,}37;1{,}5$ ), а в двоичной записи — 0|101.1111.0|01₁… (Маленькая единица крайне вероятна, но не гарантирована нашими прикидочными расчётами.)

Первое (кусочно-линейное) приближение быстрого обратного квадратного корня (c = 1,43)

Можно вычислить, чему равняется первое кусочно-линейное приближение[9] (в источнике используется не сама мантисса, а её явная часть $t=c-1$ ):

Для $x\in [0{,}5;\;c-0{,}5)$ : $y_{01}=-x+t+{\tfrac {3}{2}}=-x+c+{\tfrac {1}{2}}$ ;
Для $x\in [c-0{,}5;\;1)$ : $y_{02}=-{\tfrac {1}{2}}x+{\tfrac {1}{2}}t+{\tfrac {5}{4}}=-{\tfrac {1}{2}}x+{\tfrac {1}{2}}c+{\tfrac {3}{4}}$ ;
Для $x\in [1;\;2)$ : $y_{03}=-{\tfrac {1}{4}}x+{\tfrac {1}{2}}t+1=-{\tfrac {1}{4}}x+{\tfrac {1}{2}}c+{\tfrac {1}{2}}$ .

На бо́льших или меньших $x$ результат пропорционально меняется: при учетверении $x$ результат уменьшается ровно вдвое.

Метод Ньютона даёт[9] $f(y)={\frac {1}{y^{2}}}-x$ , $f'(y)=-{\frac {2}{y^{3}}}$ , и $y_{n+1}=y_{n}-{\frac {f(y_{n})}{f'(y_{n})}}={\frac {y_{n}(3-xy_{n}^{2})}{2}}=y_{n}(1{,}5-0{,}5\,xy_{n}^{2})$ . Функция $f(y)$ убывает и выпукла вниз, на таких функциях метод Ньютона подбирается к истинному значению слева — потому алгоритм всегда занижает ответ.

Неизвестно, откуда взялась константа 0x5F3759DF ↔ 1,4324301·2⁶³[10]. Перебором Крис Ломонт и Мэттью Робертсон выяснили[1][2], что наилучшая по предельной относительной погрешности константа для float — 0x5F375A86 ↔ 1,4324500·2⁶³, для double — 0x5FE6EB50C7B537A9. Правда, для double алгоритм бессмысленный (не даёт выигрыша в точности по сравнению с float)[2]. Константу Ломонта удалось получить и аналитически (c = 1,432450084790142642179), но расчёты довольно сложны[9][2]. Эта цифра округляется до 1,4324500, потому что единица младшего разряда равняется 1,19·10⁻⁷, и следующее число округляется до 1,4324502.

После одного шага метода Ньютона результат получается довольно точный (+0 % −0,18 %)[1][2], что для целей компьютерной графики более чем подходит (¹⁄₂₅₆ ≈ 0,39 %). Такая погрешность сохраняется на всём диапазоне нормированных дробных чисел. Два шага дают точность в 5 цифр[1], после четырёх достигается погрешность double.

Метод Ньютона не гарантирует монотонности, но компьютерный перебор показывает, что монотонность всё-таки есть.

Исходный текст (C++)

#include <iostream>

union FloatInt {
    float asFloat;
    int32_t asInt;
};

int floatToInt(float x)
{
    FloatInt r;
    r.asFloat = x;
    return r.asInt;
}

float intToFloat(int x)
{
    FloatInt r;
    r.asInt = x;
    return r.asFloat;
}


float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y;                       // evil floating point bit level hacking
    i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
    y  = * ( float * ) &i;                      // i don't know, what the fuck!
    y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration

    return y;
}

int main()
{
    int iStart = floatToInt(1.0);
    int iEnd = floatToInt(4.0);
    std::cout << "Numbers to go: " << iEnd - iStart << std::endl;
    int nProblems = 0;
    float oldResult = std::numeric_limits<float>::infinity();

    for (int i = iStart; i <= iEnd; ++i) {
        float x = intToFloat(i);
        float result = Q_rsqrt(x);
        if (result > oldResult) {
            std::cout << "Found a problem on " << x << std::endl;
            ++nProblems;
        }
    }
    std::cout << "Total problems: " << nProblems << std::endl;

    return 0;
}

Существуют аналогичные алгоритмы для других степеней, например, квадратного или кубического корня[3].

Мотивация

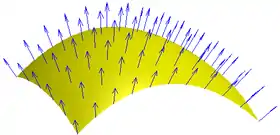
Поверхность нормалей широко используются в расчетах освещения и затенения, требующих расчета норм для векторов. Здесь показано поле векторов нормали к поверхности.

«Прямое» наложение освещения на трёхмерную модель, даже высокополигональную, даже с учётом закона Ламберта и других формул отражения и рассеивания, сразу же выдаст полигональный вид — зритель увидит разницу в освещении по рёбрам многогранника. Иногда так и нужно — если предмет действительно угловатый. А для криволинейных предметов поступают так: по углам треугольников запоминают нормаль единичной длины к криволинейной поверхности, в середине — интерполируют и нормализуют (доводят до единичной длины).

Чтобы нормализовать вектор, надо разделить все три его компонента на длину. Или, что лучше, умножить их на величину, обратную длине: $(x',y',z')=(x,y,z){\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}}}$ . За секунду должны вычисляться миллионы этих корней. До того как было создано специальное аппаратное обеспечение для обработки трансформаций и освещения, программное обеспечение вычислений могло быть медленным. В частности, в начале 1990-х, когда код был разработан, большинство вычислений с плавающей запятой отставало по производительности от операций с целыми числами.

Quake III Arena использует алгоритм быстрого обратного квадратного корня для ускорения обработки графики центральным процессором, но с тех пор алгоритм уже был реализован в некоторых специализированных аппаратных вершинных шейдерах, используя специальные программируемые матрицы (FPGA).

Даже на компьютерах 2010-х годов, в зависимости от загрузки дробного сопроцессора, скорость может быть втрое-вчетверо выше, чем с использованием стандартных функций[9].

Примечания

http://www.lomont.org/Math/Papers/2003/InvSqrt.pdf
https://web.archive.org/web/20140202234227/http://shelfflag.com/rsqrt.pdf
Hummus and Magnets
Beyond3D — Origin of Quake3’s Fast InvSqrt()
Beyond3D — Origin of Quake3’s Fast InvSqrt() — Part Two
PFRSQRT — Вычислить приблизительное значение обратной величины квадратного корня от короткого вещественного значения — Club155.ru
RSQRTSS — Compute Reciprocal of Square Root of Scalar Single-Precision Floating-Point Value
https://web.archive.org/web/20150511044204/http://www.daxia.com/bibis/upload/406Fast_Inverse_Square_Root.pdf
Швидке обчислення оберненого квадратного кореня з використанням магічної константи — аналітичний підхід
Здесь стрелка означает объяснённую выше биекцию двоичного представления целого числа и двоичного представления числа с плавающей запятой в формате IEEE 754.

Ссылки

C. Lomont, Fast inverse square root, Technical Report, 2003.
A Brief History of InvSqrt by Matthew Robertson
0x5f3759df, further investigations into accuracy and generalizability of the algorithm by Christian Plesner Hansen

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[lomont-1] ttp://www.lomont.org/Math/Papers/2003/InvSqrt.pdf

[robertson-2] ttps://web.archive.org/web/20140202234227/http://shelfflag.com/rsqrt.pdf

[hummus-3] Hummus and Magnets

[4] Beyond3D — Origin of Quake3’s Fast InvSqrt()

[5] Beyond3D — Origin of Quake3’s Fast InvSqrt() — Part Two

[6] PFRSQRT — Вычислить приблизительное значение обратной величины квадратного корня от короткого вещественного значения — Club155.ru

[7] RSQRTSS — Compute Reciprocal of Square Root of Scalar Single-Precision Floating-Point Value

[8] ttps://web.archive.org/web/20150511044204/http://www.daxia.com/bibis/upload/406Fast_Inverse_Square_Root.pdf

[moroz-9] Швидке обчислення оберненого квадратного кореня з використанням магічної константи — аналітичний підхід

[10] Здесь стрелка означает объяснённую выше биекцию двоичного представления целого числа и двоичного представления числа с плавающей запятой в формате IEEE 754.