1-планарный граф

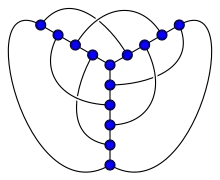
1-планарные графы первым рассматривал Рингель, который показал, что они могут быть раскрашены, не превышая семи цветов[1]. Позднее точное число цветов, необходимых для раскраски этих графов, (в худшем случае) было уменьшено до шести[2]. Пример полного графа K₆, являющегося 1-планарным, показывает, что 1-планарные графы иногда могут требовать для раскраски шести цветов. Однако доказательство достаточности шести цветом не является простым.

Раскраска вершин и граней треугольной призмы требует шесть цветов

Поводом для рассмотрения 1-планарных графов Рингелем была попытка решить вариант задачи тотальной раскраски для планарных графов, в которой раскрашиваются вершины и грани планарного графа таким образом, что никакие две смежные вершины не имеют одинаковый цвет и любые две смежные грани тоже должны быть раскрашены в разные цвета, а также цвета вершин и смежных им граней должны отличаться. Очевидно, что это можно сделать с помощью восьми красок, если применить теорему о четырёх красках для графа и его двойственного графа раздельно, применив два непересекающихся набора четырёх красок. Однако можно получить меньшее количество красок, если сформировать вспомогательный граф, имеющий по вершине для каждой вершины и грани исходного планарного графа, и в котором две вершины вспомогательного графа смежны, если они соответствуют смежным объектам заданного планарного графа. Раскраска вершин вспомогательного графа соответствует раскраске исходного планарного графа. Вспомогательный граф является 1-планарным, откуда следует, что задача Рингеля раскраски вершин и граней может быть решена с использованием шести цветов[2]. Граф K₆ не может быть получен как вспомогательный граф таким образом, но, тем не менее, задача раскраски вершин и граней иногда требует шести цветов. Например, если раскрашивать планарный граф треугольной призмы, её 6 вершин + 5 граней требует шести цветов[3].

Любой 1-планарный граф с n вершинами имеет не более 4n − 8 рёбер[4]. Более строго, каждый рисунок 1-планарного графа имеет не более n − 2 пересечений. Удаление одного ребра из каждой пересекающейся пары рёбер оставляет планарный граф, который имеет не более 3n − 6 рёбер, откуда немедленно следует граница числа рёбер 4n − 8 исходного 1-планарного графа[5]. Однако, в отличие от планарных графов (для которых все максимальные планарные графы на заданном множестве вершин имеют одинаковое число рёбер), существуют максимальные 1-планарные графы (графы, в которые нельзя добавить ребро с сохранением 1-планарности), которые имеют существенно менее 4n − 8 рёбер[6]. Граница 4n − 8 максимального возможного числа рёбер в 1-планарном графе может быть использована, чтобы показать, что полный граф K₇ с семью вершинами не является 1-планарным, поскольку этот граф имеет 21 ребро, а тогда 4n − 8 = 20 < 21 [7].

Говорят, что 1-планарный граф является оптимальным 1-планарным графом, если он имеет в точности 4n − 8 рёбер, максимально возможное число. В 1-планарном вложении оптимального 1-планарного графа непересекающиеся рёбра обязательно образуют разбиение на четырёхугольники (т.е. образуют полиэдральный граф, в котором каждая грань является четырёхугольником). Любое разбиение на четырёхугольники порождает 1-планарный граф путём добавления двух диагоналей в каждую квадратную грань. Отсюда следует, что любой оптимальный 1-планарный граф является эйлеровым (все его вершины имеют чётную степень), что наименьшая степень в таких графах — 6, и что любой оптимальный 1-планарный граф имеет по меньшей мере восемь вершин со степенью в точности шесть. Кроме того, любой оптимальный 1-планарный граф вершинно 4-связен и любое 4-вершинное сечение в таком графе является отсекающим циклом в нижележащем разбиении на четырёхугольники[8].

Графы, имеющие прямолинейные 1-планарные рисунки (то есть рисунки, в которых каждое ребро представляется прямолинейным отрезком и каждый отрезок пересекается максимум одним другим ребром), имеют слегка более сильную границу 4n − 9 максимального числа рёбер, которая достигается на бесконечном числе графов[9].

1-планарный рисунок графа коктейль-вечеринки K_2,2,2,2

Полная классификация 1-планарных полных графов, полных двудольных графов и более общих полных многодольных графов известна. Любой полный двудольный граф вида K_2,n является 1-планарным, как и любой полный трёхдольный граф вида K_1,1,n. Кроме этих бесконечных множеств, полными многодольными 1-планарными графами являются K₆, K_1,1,1,6, K_1,1,2,3, K_2,2,2,2, K_1,1,1,2,2 и их подграфы. Минимальные полные многодольные графы, не являющиеся 1-планарными, — это K_3,7, K_4,5, K_1,3,4, K_2,3,3, and K_1,1,1,1,3. Например, полный двудольный граф K_3,6 является 1-планарным, поскольку он является подграфом K_1,1,1,6, а вот K_3,7 не является 1-планарным[7].

Проверка, является ли граф 1-планарным, NP-полна[10][11], и задача остаётся NP-полной даже для граф, полученных из планарных графов путём добавления единственного ребра[12] и для графов ограниченной ширины[13].

Задача фиксированно-параметрически разрешима, если параметризовать по цикломатическому числу или по глубине дерева, так что она может быть решена за полиномиальное время, если эти параметры ограничены[13].

В отличие от теоремы Фари для планарных графов, не все 1-планарные графы могут быть нарисованы 1-планарно с отрезками прямой в качестве рёбер[14][15]. Однако проверка, можно ли нарисовать 1-планарный граф с прямыми рёбрами, может быть выполнена за полиномиальное время[16]. Кроме того, любой вершинно 3-связный 1-планарный граф имеет 1-планарный рисунок, в котором максимум одно ребро на внешней грани имеет излом. Такой рисунок может быть построен за линейное время, исходя из 1-планарного вложения графа[17]. 1-планарные графы имеют ограниченную книжную толщину[18], но некоторые 1-планарные графы, включая K_2,2,2,2, имеют книжную толщину по меньшей мере четыре[19].

1-планарные графы имеют ограниченную локальную древесную ширину, что означает, что существует (линейная) функция f, такая, что 1-планарные графы диаметра d имеют древесную ширину, не превосходящую f(d). То же свойство имеет место для более общих графов, которые можно вложить в поверхность ограниченного рода с ограниченным числом пересечений на ребро. Они также имеют сепараторы, небольшое множество вершин, удаление которых разбивает граф на связные компоненты, размер которых составляет постоянную дробную часть от всего графа. Опираясь на эти свойства многочисленные алгоритмы для планарных графов, такие как техника Бренды Бейкер (Brenda Sue Baker – американская женщина-математик ) для построения аппроксимационных алгоритмов, могут быть расширены для 1-планарных графов. Например, этот метод приводит к приближенной схеме полиномиального времени для нахождения наибольшего независимого множества 1-планарного графа[20].

Класс графов, аналогичных внешнепланарным графам для 1-планарности, называется внешне 1-планарные графы. Это графы, которые можно нарисовать на диске с вершинами на границе диска и с рёбрами, имеющими максимум одно пересечение на ребро. Эти графы всегда могут быть нарисованы (в виде внешне 1-планарного графа) с прямыми рёбрами и пересечениями под прямыми углами[21]. При помощи динамического программирования на SPQR-дереве заданного графа можно проверить, не является ли граф внешне 1-планарным, за линейное время[22][23]. Трёхсвязные компоненты графа (узлы дерева SPQR) могут состоять только из циклов, бондграфов и полных графов с четырьмя вершинами, откуда следует, что внешне 1-планарные графы являются планарными и имеют древесную ширину максимум три. В отличие от 1-планарных графов, внешне 1-планарные графы имеют характеризацию в терминах миноров графа — граф является внешне 1-планарным тогда и только тогда, когда в нём нет ни одного из пяти запрещённых миноров[23].

Классу 1-планарных графов принадлежат графы 4-карт, графы, образованные из смежных регионов плоскости с условием, что никакая точка не лежит на границе более четырёх регионов (вершины (регионы) соединены ребром, если регионы граничат). И обратно — любой оптимальный 1-планарный граф является графом 4-карты. Однако 1-планарные графы, не являющиеся оптимальными 1-планарными, могут и не быть графами карт[24].

1-планарные графы обобщаются до k-планарных графов, в которых каждое ребро пересекается другими рёбрами не более k раз. Рингель определил локальное число пересечений графа G как наименьшее неотрицательное k, такое, что G имеет k-планарный рисунок. Поскольку локальное число пересечений равно наибольшей степени графа пересечений рёбер оптимального рисунка, а толщина (минимальное число планарных графов, на которые можно разложить рёбра) может рассматриваться как хроматическое число графа пересечений подходящего рисунка, из теоремы Брукса следует, что толщина не больше чем на единицу превышает локальное число пересечений[25]. k-планарные графы с n вершинами имеют максимум O(k^1/2n) рёбер[26] и древесную ширину O((kn)^1/2)[27]. Неглубокий минор k-планарного графа с глубиной d сам является (2d + 1)k-планарным, так что неглубокие миноры 1-планарных графов и k-планарных графов являются разреженными графами, здесь имеется в виду, что 1-планарные и k-планарные графы имеют ограниченное расшериние[28].

Для непланарных графов также можно задать параметр число пересечений, минимальное число рёбер, которые пересекаются в любом рисунке графа. Граф с числом пересечений k обязательно k-планарен, но обратное не обязательно верно. Например, Граф Хивуда имеет число пересечений 3, но не обязательно эти пересечения должны быть с одним ребром, он 1-планарен и может быть нарисован с одновременной опримизацией общего числа пересечений и пересечений на одно ребро.

Другое связанное понятие для непланарных графов — перекос, минимальное число рёбер, которые нужно удалить, чтобы сделать граф планарным.

• Gerhard Ringel. Ein Sechsfarbenproblem auf der Kugel (нем.) // Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. — 1965. — Bd. 29. — S. 107–117. — doi:10.1007/BF02996313.
• Michael O. Albertson, Bojan Mohar. Coloring vertices and faces of locally planar graphs // Graphs and Combinatorics. — 2006. — Т. 22, вып. 3. — С. 289–295. — doi:10.1007/s00373-006-0653-4.
• H. Schumacher. Zur Struktur 1-planarer Graphen (нем.) // Mathematische Nachrichten. — 1986. — Bd. 125. — S. 291–300.
• Július Czap, Dávid Hudák. On drawings and decompositions of 1-planar graphs // Electronic Journal of Combinatorics. — 2013. — Т. 20, вып. 2.
• Franz Josef Brandenburg, David Eppstein, Andreas Gleißner, Michael T. Goodrich, Kathrin Hanauer, Josef Reislhuber. Proc. 20th Int. Symp. Graph Drawing / Walter Didimo, Maurizio Patrignani. — 2013.
• Yusuke Suzuki. Re-embeddings of maximum 1-planar graphs // SIAM Journal on Discrete Mathematics. — 2010. — Т. 24, вып. 4. — С. 1527–1540. — doi:10.1137/090746835.
• Walter Didimo. Density of straight-line 1-planar graph drawings // Information Processing Letters. — 2013. — Т. 113, вып. 7. — С. 236–240. — doi:10.1016/j.ipl.2013.01.013.
• Július Czap, Dávid Hudák. 1-planarity of complete multipartite graphs // Discrete Applied Mathematics. — 2012. — Т. 160, вып. 4-5. — С. 505–512. — doi:10.1016/j.dam.2011.11.014.
• Alexander Grigoriev, Hans L. Bodlaender. Algorithms for graphs embeddable with few crossings per edge // Algorithmica. — 2007. — Т. 49, вып. 1. — С. 1–11. — doi:10.1007/s00453-007-0010-x.
• Vladimir P. Korzhik, Bojan Mohar. Graph Drawing: 16th International Symposium, GD 2008, Heraklion, Crete, Greece, September 21-24, 2008, Revised Papers / Ioannis G. Tollis, Maurizio Patrignani. — Springer, 2009. — Т. 5417. — С. 302–312. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-00219-9_29.
• Sergio Cabello, Bojan Mohar. Adding one edge to planar graphs makes crossing number and 1-planarity hard. — 2012. — arXiv:1203.5944. Расширенная версия статьи 17-го ACM Симпозиума по Вычислительной геометрии, 2010.
• Michael J. Bannister, Sergio Cabello, David Eppstein. Algorithms and Data Structures Symposium (WADS 2013). — 2013.
• Michael Bekos, Michael Kaufmann, Christian Zielke. Proc. 23rd International Symposium on Graph Drawing and Network Visualization (GD 2015). — 2015. — С. 113–125.
• Vida Dujmović, David Eppstein, David R. Wood. Proc. 23rd International Symposium on Graph Drawing and Network Visualization (GD 2015). — 2015. — С. 77–88.
• О.В. Бородин. Решение задачи Рингеля о вершинно-граневой раскраске плоских графов и о раскраске 1-планарных графов. // Методы дискретного анализа в изучении реализаций логических функций. — Новосибирск: Институт математики СО АН СССР, 1984. — Вып. 41. — С. 12–26, 108.
• Roger B. Eggleton. Rectilinear drawings of graphs // Utilitas Mathematica. — 1986. — Т. 29. — С. 149–172.
• Carsten Thomassen. Rectilinear drawings of graphs // Journal of Graph Theory. — 1988. — Т. 12, вып. 3. — С. 335–341. — doi:10.1002/jgt.3190120306.
• Seok-Hee Hong, Peter Eades, Giuseppe Liotta, Sheung-Hung Poon. Computing and Combinatorics: 18th Annual International Conference, COCOON 2012, Sydney, Australia, August 20-22, 2012, Proceedings / Joachim Gudmundsson, Julián Mestre, Taso Viglas. — Springer, 2012. — Т. 7434. — С. 335–346. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-32241-9_29.
• Md. Jawaherul Alam, Franz J. Brandenburg, Stephen G. Kobourov. Graph Drawing: 21st International Symposium, GD 2013, Bordeaux, France, September 23-25, 2013, Revised Selected Papers. — 2013. — Т. 8242. — С. 83–94. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-319-03841-4_8.
• Michael A. Bekos, Till Bruckdorfer, Michael Kaufmann, Chrysanthi Raftopoulou. Algorithms – ESA 2015. — Springer, 2015. — Т. 9294. — С. 130–141. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-662-48350-3_12.
• Hooman Reisi Dehkordi, Peter Eades. Every outer-1-plane graph has a right angle crossing drawing // International Journal of Computational Geometry & Applications. — 2012. — Т. 22, вып. 6. — С. 543–557. — doi:10.1142/S021819591250015X.
• Seok-Hee Hong, Peter Eades, Naoki Katoh, Giuseppe Liotta, Pascal Schweitzer, Yusuke Suzuki. 21st International Symposium, GD 2013, Bordeaux, France, September 23-25, 2013, Revised Selected Papers / Stephen Wismath, Alexander Wolff. — 2013. — Т. 8242. — С. 71–82. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-319-03841-4_7.
• Christopher Auer, Christian Bachmaier, Franz J. Brandenburg, Andreas Gleißner, Kathrin Hanauer, Daniel Neuwirth, Josef Reislhuber. 21st International Symposium, GD 2013, Bordeaux, France, September 23-25, 2013, Revised Selected Papers / Stephen Wismath, Alexander Wolff. — 2013. — Т. 8242. — С. 107–118. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-319-03841-4_10.
• Zhi-Zhong Chen, Michelangelo Grigni, Christos H. Papadimitriou. Map graphs // Journal of the ACM. — 2002. — Т. 49, вып. 2. — С. 127–138. — doi:10.1145/506147.506148.
• Paul Kainen. Thickness and coarseness of graphs // Abh. Math. Sem. Univ. Hamburg. — 1973. — Т. 39. — С. 88-95. — doi:10.1007/BF02992822.
• János Pach, Géza Tóth. Graphs drawn with few crossings per edge // Combinatorica. — 1997. — Т. 17, вып. 3. — С. 427–439. — doi:10.1007/BF01215922.
• Jaroslav Nešetřil, Patrice Ossona de Mendez. Sparsity: Graphs, Structures, and Algorithms. — Springer, 2012. — Т. 28. — С. 321, Theorem 14.4. — (Algorithms and Combinatorics). — ISBN 978-3-642-27874-7. — doi:10.1007/978-3-642-27875-4.